Minkowski distance
Encyclopedia
The Minkowski distance is a metric
on Euclidean space
which can be considered as a generalization of both the Euclidean distance
and the Manhattan distance.
is defined as:
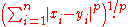
The Minkowski distance is a metric
as a result of the Minkowski inequality
.
Minkowski distance is typically used with p being 1 or 2. The latter is the Euclidean distance
, while the former is sometimes known as the Manhattan distance. In the limiting case of p reaching infinity we obtain the Chebyshev distance
:
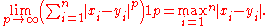
The following figure shows unit circles with various values of p:

Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
which can be considered as a generalization of both the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
and the Manhattan distance.
Definition
The Minkowski distance of order p between two pointsis defined as:
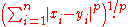
The Minkowski distance is a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
as a result of the Minkowski inequality
Minkowski inequality
In mathematical analysis, the Minkowski inequality establishes that the Lp spaces are normed vector spaces. Let S be a measure space, let 1 ≤ p ≤ ∞ and let f and g be elements of Lp...
.
Minkowski distance is typically used with p being 1 or 2. The latter is the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
, while the former is sometimes known as the Manhattan distance. In the limiting case of p reaching infinity we obtain the Chebyshev distance
Chebyshev distance
In mathematics, Chebyshev distance , Maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension...
:
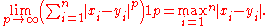
The following figure shows unit circles with various values of p:



