Metric (mathematics)
Encyclopedia
In mathematics
, a metric or distance function is a function
which defines a distance
between elements of a set. A set with a metric is called a metric space
. A metric induces a topology
on a set but not all topologies can be generated by a metric. When a topological space
has a topology that can be described by a metric, we say that the topological space is metrizable.
In differential geometry, the word "metric" is also used to refer to a structure defined only on a differentiable manifold
which is more properly termed a metric tensor
(or Riemannian or pseudo-Riemannian metric).
(called the distance function or simply distance)
d : X × X → R
(where R is the set of real number
s). For all x, y, z in X, this function is required to satisfy the following conditions:
The first condition is implied by the others.
A metric is called an ultrametric if it satisfies the following stronger version of the triangle inequality where points can never fall 'between' other points:
A metric d on X is called intrinsic
if any two points x and y in X can be joined by a curve
with length arbitrarily close to d(x, y).
For sets on which an addition + : X × X → X is defined,
d is called a translation invariant metric if
for all x, y and a in X.
is a homeomorphism
(uniform isomorphism
).
For example, if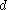
is a metric, then 
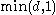and 
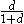are metrics equivalent to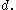 
See also notions of metric space equivalence.
Given a normed vector space
we can define a metric on X by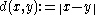
.
The metric d is said to be induced by the norm
.
Conversely if a metric d on a vector space
X satisfies the properties
then we can define a norm
on X by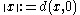
Similarly, a seminorm induces a pseudometric (see below), and a homogeneous, translation invariant pseudometric induces a seminorm.
pseudometrics often come from seminorms on vector spaces, and so it is natural to call them "semimetrics". This conflicts with the use of the term in topology
.
. Such a function is called an extended metric. Every extended metric can be transformed to a finite metric such that the metric spaces are equivalent as far as notions of topology
(such as continuity or convergence
) are concerned. This can be done using a subadditive
monotically increasing bounded function which is zero at zero, e.g. d′(x, y) = d(x, y) / (1 + d(x, y)) or d′′(x, y) = min(1, d(x, y))).
The requirement that the metric take values in[0,∞) can even be relaxed to consider metrics with values in other directed set
s. The reformulation of the axioms in this case leads to the construction of uniform space
s: topological spaces with an abstract structure enabling one to compare the local topologies of different points.
This is the most common generalization of metrics. In some contexts, pseudometrics are referred to as semimetrics because of their relation to seminorms.
If d is a quasimetric on X, a metric d' on X can be formed by taking
Quasimetrics are common in real life. For example, given a set X of mountain villages, the typical walking times between elements of X form a quasimetric because travel up hill takes longer than travel down hill. Another example is a taxicab geometry
topology having one-way streets, where a path from point A to point B comprises a different set of streets than a path from B to A. Nevertheless, this notion is rarely used in mathematics, and its name is not entirely standardized.
A quasimetric on the reals can be defined by setting
The topological space underlying this quasimetric space is the Sorgenfrey line.
Some authors work with a weaker form of the triangle inequality, such as:
The ρ-inframetric inequality implies the ρ-relaxed triangle inequality (assuming the first axiom), and the ρ-relaxed triangle inequality implies the 2ρ-inframetric inequality. Semimetrics satisfying these equivalent conditions have sometimes been referred to as "quasimetrics", "nearmetrics" or inframetrics.
The ρ-inframetric inequalities were introduced to model round-trip delay time
s in the internet
. The triangle inequality implies the 2-inframetric inequality, and the ultrametric inequality is exactly the 1-inframetric inequality.
This is not a standard term. Sometimes it is used to refer to other generalizations of metrics such as pseudosemimetrics or pseudometrics; in translations of Russian books it sometimes appears as "prametric".
Any premetric gives rise to a topology as follows. For a positive real r, the open r-ball centred at a point p is defined as
A set is open if for any point p in the set there is an r-ball centred at p which is contained in the set. In general, the open r-balls themselves need not be open sets with respect to this topology. In fact, the interior of an r-ball may be empty. Thus every premetric space is a topological space, and in fact a sequential space
.
As for metrics, the distance between two sets A and B, is defined as
This defines a premetric on the power set of a premetric space. If we start with a (pseudosemi-)metric space, we get a pseudosemimetric, i.e. a symmetric premetric.
Any premetric gives rise to a preclosure operator
cl as follows:
.
Sets equipped with an extended pseudoquasimetric were studied by William Lawvere
as "generalized metric spaces". From a categorical
point of view, the extended pseudometric spaces and the extended pseudoquasimetric spaces, along with their corresponding nonexpansive maps, are the best behaved of the metric space categories. One can take arbitrary products and coproducts and form quotient objects within the given category. If one drops "extended", one can only take finite products and coproducts. If one drops "pseudo", one cannot take quotients. Approach space
s are a generalization of metric spaces that maintains these good categorical properties.
s, which can be thought of as "infinitesimal" metric functions. They are defined as inner products on the tangent space
with an appropriate differentiability requirement. While these are not metric functions as defined in this article, they induce metric functions by integration
. A manifold
with a metric tensor is called a Riemannian manifold
. If one drops the positive definiteness requirement of inner product spaces, then one obtains a pseudo-Riemannian metric tensor
, which integrates to a pseudo-semimetric. These are used in the geometric study of the theory of relativity
, where the tensor is also called the "invariant distance".
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a metric or distance function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which defines a distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between elements of a set. A set with a metric is called a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. A metric induces a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on a set but not all topologies can be generated by a metric. When a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
has a topology that can be described by a metric, we say that the topological space is metrizable.
In differential geometry, the word "metric" is also used to refer to a structure defined only on a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
which is more properly termed a metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
(or Riemannian or pseudo-Riemannian metric).
Definition
A metric on a set X is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(called the distance function or simply distance)
d : X × X → R
(where R is the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s). For all x, y, z in X, this function is required to satisfy the following conditions:
- d(x, y) ≥ 0 (non-negativity)
- d(x, y) = 0 if and only if x = y (identity of indiscerniblesIdentity of indiscerniblesThe identity of indiscernibles is an ontological principle which states that two or more objects or entities are identical if they have all their properties in common. That is, entities x and y are identical if any predicate possessed by x is also possessed by y and vice versa...
. Note that condition 1 and 2 together produce positive definiteness) - d(x, y) = d(y, x) (symmetrySymmetric relationIn mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
) - d(x, z) ≤ d(x, y) + d(y, z) (subadditivity / triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
).
The first condition is implied by the others.
A metric is called an ultrametric if it satisfies the following stronger version of the triangle inequality where points can never fall 'between' other points:
- For all x, y, z in X, d(x, z) ≤ max(d(x, y), d(y, z))
A metric d on X is called intrinsic
Intrinsic metric
In the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are a given distance from each other, it is natural to expect that one should be able to get from one point to another along a path whose arclength is equal to that distance...
if any two points x and y in X can be joined by a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
with length arbitrarily close to d(x, y).
For sets on which an addition + : X × X → X is defined,
d is called a translation invariant metric if
- d(x, y) = d(x + a, y + a)
for all x, y and a in X.
Examples
- The discrete metricDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
: if x = y then d(x,y) = 0. Otherwise, d(x,y) = 1. - The Euclidean metric is translation and rotation invariant.
- The taxicab metricTaxicab geometryTaxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
is translation invariant. - More generally, any metric induced by a normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
is translation invariant. - If
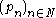is a sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of seminorms defining a (locally convex) topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
E, then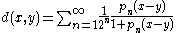
- is a metric defining the same topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. (One can replace
by any summable sequenceAbsolute convergenceIn mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
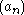of strictly positive numbers.)
- Graph metric, a metric defined in terms of distances in a certain graph.
- The Hamming distanceHamming distanceIn information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
in coding theory. - The Fubini–Study metric on complex projective spaceComplex projective spaceIn mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
.
Equivalence of metrics
For a given set X, two metrics d1 and d2 are called topologically equivalent (uniformly equivalent) if the identity mapping- id: (X,d1) → (X,d2)
is a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
(uniform isomorphism
Uniform isomorphism
In the mathematical field of topology a uniform isomorphism or uniform homeomorphism is a special isomorphism between uniform spaces which respects uniform properties.-Definition:...
).
For example, if
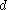is a metric, then 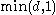and 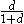are metrics equivalent to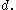 See also notions of metric space equivalence.
Metrics on vector spaces
Norms on vector spaces are equivalent to certain metrics, namely homogeneous, translation-invariant ones. In other words, every norm determines a metric, and some metrics determine a norm.Given a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
we can define a metric on X by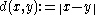.The metric d is said to be induced by the norm
.Conversely if a metric d on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
X satisfies the properties
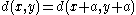(translation invariance)
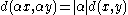(homogeneity)
then we can define a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
on X by
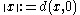
Similarly, a seminorm induces a pseudometric (see below), and a homogeneous, translation invariant pseudometric induces a seminorm.
Generalized metrics
There are numerous ways of relaxing the axioms of metrics, giving rise to various notions of generalized metric spaces. These generalizations can also be combined. The terminology used to describe them is not completely standardized. Most notably, in functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
pseudometrics often come from seminorms on vector spaces, and so it is natural to call them "semimetrics". This conflicts with the use of the term in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Extended metrics
Some authors allow the distance function d to attain the value ∞, i.e. distances are non-negative numbers on the extended real number lineExtended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
. Such a function is called an extended metric. Every extended metric can be transformed to a finite metric such that the metric spaces are equivalent as far as notions of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
(such as continuity or convergence
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
) are concerned. This can be done using a subadditive
Subadditive function
In mathematics, subadditivity is a property of a function that states, roughly, that evaluating the function for the sum of two elements of the domain always returns something less than or equal to the sum of the function's values at each element. There are numerous examples of subadditive...
monotically increasing bounded function which is zero at zero, e.g. d′(x, y) = d(x, y) / (1 + d(x, y)) or d′′(x, y) = min(1, d(x, y))).
The requirement that the metric take values in
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
s. The reformulation of the axioms in this case leads to the construction of uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s: topological spaces with an abstract structure enabling one to compare the local topologies of different points.
Pseudometrics
A pseudometric on X is a function d : X × X → R which satisfies the axioms for a metric, except that instead of the second (identity of indiscernibles) only d(x,x)=0 for all x is required. In other words, the axioms for a pseudometric are:- d(x, y) ≥ 0
- d(x, x) = 0 (but possibly
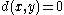for some distinct values 
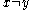.) - d(x, y) = d(y, x)
- d(x, z) ≤ d(x, y) + d(y, z).
This is the most common generalization of metrics. In some contexts, pseudometrics are referred to as semimetrics because of their relation to seminorms.
Quasimetrics
Occasionally, a quasimetric is defined as a function that satisfies all axioms for a metric with the possible exception of symmetry:- d(x, y) ≥ 0
- d(x, y) = 0 if and only if x = y
-
d(x, y) = d(y, x)(dropped) - d(x, z) ≤ d(x, y) + d(y, z).
If d is a quasimetric on X, a metric d
- d
' (x, y) = (d(x, y) + d(y, x)).
Quasimetrics are common in real life. For example, given a set X of mountain villages, the typical walking times between elements of X form a quasimetric because travel up hill takes longer than travel down hill. Another example is a taxicab geometry
Taxicab geometry
Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
topology having one-way streets, where a path from point A to point B comprises a different set of streets than a path from B to A. Nevertheless, this notion is rarely used in mathematics, and its name is not entirely standardized.
A quasimetric on the reals can be defined by setting
- d(x, y) = y − x if y ≥ x, and
- d(x, y) = 1 otherwise.
The topological space underlying this quasimetric space is the Sorgenfrey line.
Semimetrics
A semimetric on X is a function d : X × X → R that satisfies the first three axioms, but not necessarily the triangle inequality:- d(x, y) ≥ 0
- d(x, y) = 0 if and only if x = y
- d(x, y) = d(y, x)
Some authors work with a weaker form of the triangle inequality, such as:
- d(x, z) ≤ ρ (d(x, y) + d(y, z)) (ρ-relaxed triangle inequality)
- d(x, z) ≤ ρ max(d(x, y), d(y, z)) (ρ-inframetric inequality).
The ρ-inframetric inequality implies the ρ-relaxed triangle inequality (assuming the first axiom), and the ρ-relaxed triangle inequality implies the 2ρ-inframetric inequality. Semimetrics satisfying these equivalent conditions have sometimes been referred to as "quasimetrics", "nearmetrics" or inframetrics.
The ρ-inframetric inequalities were introduced to model round-trip delay time
Round-trip delay time
In telecommunications, the round-trip delay time or round-trip time is the length of time it takes for a signal to be sent plus the length of time it takes for an acknowledgment of that signal to be received...
s in the internet
Internet
The Internet is a global system of interconnected computer networks that use the standard Internet protocol suite to serve billions of users worldwide...
. The triangle inequality implies the 2-inframetric inequality, and the ultrametric inequality is exactly the 1-inframetric inequality.
Premetrics
Relaxing the last three axioms leads to the notion of a premetric, i.e. a function satisfying the following conditions:- d(x, y) ≥ 0
- d(x, x) = 0
This is not a standard term. Sometimes it is used to refer to other generalizations of metrics such as pseudosemimetrics or pseudometrics; in translations of Russian books it sometimes appears as "prametric".
Any premetric gives rise to a topology as follows. For a positive real r, the open r-ball centred at a point p is defined as
- Br(p) = { x | d(x, p) < r }.
A set is open if for any point p in the set there is an r-ball centred at p which is contained in the set. In general, the open r-balls themselves need not be open sets with respect to this topology. In fact, the interior of an r-ball may be empty. Thus every premetric space is a topological space, and in fact a sequential space
Sequential space
In topology and related fields of mathematics, a sequential space is a topological space that satisfies a very weak axiom of countability. Sequential spaces are the most general class of spaces for which sequences suffice to determine the topology....
.
As for metrics, the distance between two sets A and B, is defined as
- d(A, B) = infx∊A, y∊B d(x, y).
This defines a premetric on the power set of a premetric space. If we start with a (pseudosemi-)metric space, we get a pseudosemimetric, i.e. a symmetric premetric.
Any premetric gives rise to a preclosure operator
Preclosure operator
In topology, a preclosure operator, or Čech closure operator is a map between subsets of a set, similar to a topological closure operator, except that it is not required to be idempotent...
cl as follows:
- cl(A) = { x | d(x, A) = 0 }.
Pseudoquasimetrics
The presyllables pseudo-, quasi- and semi- can also be combined, e.g., a pseudoquasimetric (sometimes called hemimetric) relaxes both the indiscernibility axiom and the symmetry axiom and is simply a premetric satisfying the triangle inequality. For pseudoquasimetric spaces the open r-balls form a basis of open sets. A very basic example of a pseudoquasimetric space is the set {0,1} with the premetric given by d(0,1) = 1 and d(1,0) = 0. The associated topological space is the Sierpiński spaceSierpinski space
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
.
Sets equipped with an extended pseudoquasimetric were studied by William Lawvere
William Lawvere
Francis William Lawvere is a mathematician known for his work in category theory, topos theory and the philosophy of mathematics.-Biography:...
as "generalized metric spaces". From a categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
point of view, the extended pseudometric spaces and the extended pseudoquasimetric spaces, along with their corresponding nonexpansive maps, are the best behaved of the metric space categories. One can take arbitrary products and coproducts and form quotient objects within the given category. If one drops "extended", one can only take finite products and coproducts. If one drops "pseudo", one cannot take quotients. Approach space
Approach space
In topology, approach spaces are a generalization of metric spaces, based on point-to-set distances, instead of point-to-point distances. They were introduced by in 1989.-Definition:...
s are a generalization of metric spaces that maintains these good categorical properties.
Important cases of generalized metrics
In differential geometry, one considers metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
s, which can be thought of as "infinitesimal" metric functions. They are defined as inner products on the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
with an appropriate differentiability requirement. While these are not metric functions as defined in this article, they induce metric functions by integration
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
. A manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with a metric tensor is called a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. If one drops the positive definiteness requirement of inner product spaces, then one obtains a pseudo-Riemannian metric tensor
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, which integrates to a pseudo-semimetric. These are used in the geometric study of the theory of relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
, where the tensor is also called the "invariant distance".
External links
pages 91–94 explain the use of quasimetrics in financeFinance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
.