Chebyshev distance
Encyclopedia
In mathematics
, Chebyshev distance (or Tchebychev distance), Maximum metric, or L∞ metric
is a metric
defined on a vector space
where the distance
between two vector
s is the greatest of their differences along any coordinate dimension. It is named after Pafnuty Chebyshev
.
It is also known as chessboard distance, since in the game of chess
the minimum number of moves needed by a king
to go from one square on a chessboard
to another equals the Chebyshev distance between the centers of the squares, if the squares have side length one, as represented in 2-D spatial coordinates with axes aligned to the edges of the board. For example, the Chebyshev distance between F6 and E2 equals 4.
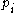and 
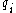, respectively, is
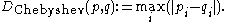
This equals the limit of the Lp metrics
:
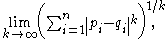
hence it is also known as the L∞ metric.
Mathematically, the Chebyshev distance is a metric
induced by the supremum norm or uniform norm. It is an example of an injective metric
.
In two dimensions, i.e. plane geometry
, if the points p and q have Cartesian coordinates
and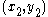 
, their Chebyshev distance is
Under this metric, a circle
of radius
r, which is the set of points with Chebyshev distance r from a center point, is a square whose sides have the length 2r and are parallel to the coordinate axes.
On a chess board, where one is using a discrete Chebyshev distance, rather than a continuous one, the circle of radius r is a square of side lengths 2r, measuring from the centers of squares, and thus each side contains 2r+1 squares; for example, the circle of radius 1 on a chess board is a 3×3 square.
The two dimensional Manhattan distance also has circles in the form of squares, with sides of length √2r, oriented at an angle of π/4 (45°) to the coordinate axes, so the planar Chebyshev distance can be viewed as equivalent by rotation and scaling to the planar Manhattan distance.
However, this equivalence between L1 and L∞ metrics does not generalize to higher dimensions. A sphere
formed using the Chebyshev distance as a metric is a cube
with each face perpendicular to one of the coordinate axes, but a sphere formed using Manhattan distance is an octahedron
: these are dual polyhedra, but among cubes, only the square (and 1-dimensional line segment) are self-dual polyhedra.
The Chebyshev distance is sometimes used in warehouse logistics
.
On a grid (such as a chessboard), the points at a Chebyshev distance of 1 of a point are the Moore neighborhood
of that point.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Chebyshev distance (or Tchebychev distance), Maximum metric, or L∞ metric
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
is a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
defined on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
where the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between two vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
s is the greatest of their differences along any coordinate dimension. It is named after Pafnuty Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
.
It is also known as chessboard distance, since in the game of chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
the minimum number of moves needed by a king
King (chess)
In chess, the king is the most important piece. The object of the game is to trap the opponent's king so that its escape is not possible . If a player's king is threatened with capture, it is said to be in check, and the player must remove the threat of capture on the next move. If this cannot be...
to go from one square on a chessboard
Chessboard
A chessboard is the type of checkerboard used in the board game chess, and consists of 64 squares arranged in two alternating colors...
to another equals the Chebyshev distance between the centers of the squares, if the squares have side length one, as represented in 2-D spatial coordinates with axes aligned to the edges of the board. For example, the Chebyshev distance between F6 and E2 equals 4.
Definition
The Chebyshev distance between two vectors or points p and q, with standard coordinates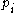 and 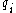, respectively, is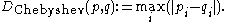This equals the limit of the Lp metrics
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
:
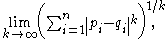
hence it is also known as the L∞ metric.
Mathematically, the Chebyshev distance is a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
induced by the supremum norm or uniform norm. It is an example of an injective metric
Injective metric space
In metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher-dimensional vector spaces...
.
In two dimensions, i.e. plane geometry
Plane geometry
In mathematics, plane geometry may refer to:*Euclidean plane geometry, the geometry of plane figures,*geometry of a plane,or sometimes:*geometry of a projective plane, most commonly the real projective plane but possibly the complex projective plane, Fano plane or others;*geometry of the hyperbolic...
, if the points p and q have Cartesian coordinates
and 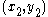, their Chebyshev distance isUnder this metric, a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
of radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
r, which is the set of points with Chebyshev distance r from a center point, is a square whose sides have the length 2r and are parallel to the coordinate axes.
On a chess board, where one is using a discrete Chebyshev distance, rather than a continuous one, the circle of radius r is a square of side lengths 2r, measuring from the centers of squares, and thus each side contains 2r+1 squares; for example, the circle of radius 1 on a chess board is a 3×3 square.
Properties
In one dimension, all Lp metrics are equal – they are just the absolute value of the difference.The two dimensional Manhattan distance also has circles in the form of squares, with sides of length √2r, oriented at an angle of π/4 (45°) to the coordinate axes, so the planar Chebyshev distance can be viewed as equivalent by rotation and scaling to the planar Manhattan distance.
However, this equivalence between L1 and L∞ metrics does not generalize to higher dimensions. A sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
formed using the Chebyshev distance as a metric is a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
with each face perpendicular to one of the coordinate axes, but a sphere formed using Manhattan distance is an octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
: these are dual polyhedra, but among cubes, only the square (and 1-dimensional line segment) are self-dual polyhedra.
The Chebyshev distance is sometimes used in warehouse logistics
Logistics
Logistics is the management of the flow of goods between the point of origin and the point of destination in order to meet the requirements of customers or corporations. Logistics involves the integration of information, transportation, inventory, warehousing, material handling, and packaging, and...
.
On a grid (such as a chessboard), the points at a Chebyshev distance of 1 of a point are the Moore neighborhood
Moore neighborhood
In cellular automata, the Moore neighborhood comprises the eight cells surrounding a central cell on a two-dimensional square lattice. The neighborhood is named after Edward F. Moore, a pioneer of cellular automata theory. It is one of the two most commonly used neighborhood types, the other one...
of that point.