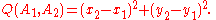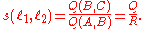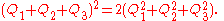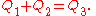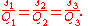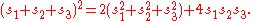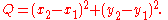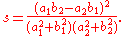
Rational trigonometry
Encyclopedia
Rational trigonometry is a recently introduced approach to trigonometry
that eschews all transcendental function
s (such as sine and cosine) and all proportional measurements of angles. In place of angles, it characterizes the separation between lines by a quantity called the "spread", which is a rational function of their slopes
. In place of the classical transcendental functions, it introduces a number of "laws" between the lengths and spreads of lines bound by various geometric configurations, notably triangles.
Rational trigonometry was introduced by Prof. Norman J. Wildberger in his 2005 book Divine Proportions: Rational Trigonometry to Universal Geometry. The book is purposefully critical of traditional mathematics. One of the main claims the author makes is that the field of trigonometry is being taught and applied using choices in measurements and relations (such as angles and transcendental functions) that are arbitrarily complicated, are not necessary in order to reason about most concepts of the field, nor are they needed for most practical applications.
The author proposes new basic measurements on which to base the field itself and related applications (namely, the square of distance instead of the plain distance between two points, and the spread instead of the angle between two lines) and goes on to prove an array of theorems and laws to work with these measurements.
From there, the author rebuilds a great part of Euclidean geometry
on top of his new proposed measurements, using only rational equivalences, which allow him to avoid any assumptions about the underlying scalar field
. This is the Universal Geometry part of the book, where most classical findings of geometry are shown to be applicable to any field, including the field of rational numbers or finite field
s.
Wildberger holds a Ph.D. in mathematics from Yale University
, and taught at Stanford University
from 1984 to 1986 and at the University of Toronto
from 1986 to 1989; he is currently an associate professor of mathematics at the University of New South Wales
, Australia
.
, rational trigonometry uses as its fundamental units quadrance (square of distance) and spread (square of sine
of angle). This choice of variables enables calculations to produce output results whose complexity matches that of the input data. For instance, in a typical trigonometry problem if rational numbers are assigned to all quadrances and spreads, then the calculated results will be rational numbers (or roots of rational numbers).
This rationality is obtained at the expense of linearity. Unlike the traditional distance and angle units, doubling or halving a quadrance or spread does not double or halve a length or a rotation. Similarly, the sum of two lengths or rotations is not the sum of their individual quadrances or spreads.
For distinction, Wildberger refers to the traditional trigonometry as classical trigonometry.
It is otherwise broadly based on Cartesian analytic geometry
, with a point
defined as an ordered pair
(x, y) and a line
as a general linear equation
The mathematics of rational trigonometry is, applications aside, a special instance of the description of geometry in terms of linear algebra
(using rational methods such as dot product
s and quadratic form
s), but students who are first learning trigonometry are often not taught about the use of linear algebra in geometry. Changing this state of affairs is a stated aim of Wildberger's book (to paraphrase his comments).
, not just the field of real number
s.
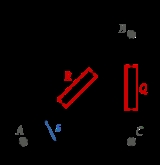
Quadrance and distance are concerned with the separation of points. Quadrance differs from standard distance in that it squares the distance. Most immediately, this means that calculating the distance (or, more accurately, quadrance) between two points in 2-dimensional space is easier, as there is no need to find the square root of the sum of the squares of the differences in the x and y coordinates.
In the (x, y)-plane, the quadrance Q(A1, A2) for the points A1 and A2 is defined as
Spread, a measure of the separation of lines, is a dimensionless number in the range [0, 1]. The value of the spread is the square of the sine of the angle.
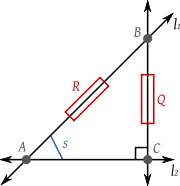
Suppose two lines, ℓ 1 and ℓ 2, intersect at the point A as shown at right. Choose a point B ≠ A on ℓ 1 and let C be the foot of the perpendicular from B to ℓ 2. Then the spread s is
, whereas angle describes a relationship between two rays emanating from a common point.
The spread is the square of the sine of the angle.
Spread is not proportional to degrees or radians, and has a period of 180 degrees (π radians).
In the following five formulas, we have a triangle made of three points A1, A2, A3, . The spreads of the angles at those points are s1, s2, s3, , and Q1, Q2, Q3, are the quadrances of the triangle sides opposite A1, A2, and A3, respectively. As in classical trigonometry, if we know three of the six elements s1, s2, s3, , Q1, Q2, Q3, and these three are not the three s', then we can compute the other three.
This formula comes from applying is equivalent to using Heron's formula, the condition for collinearity being that the triangle formed by the three points has zero area.
It can either be proved by analytic geometry
(the preferred means within rational trigonometry) or derived from Heron's formula, using the condition for collinearity that the triangle formed by the three points has zero area.
The line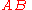 
has the general form:
where the (non-unique) parameters a, b and c, can be expressed in terms of the coordinates of points A and B as:
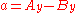
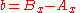
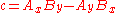
so that, everywhere on the line:
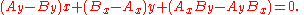
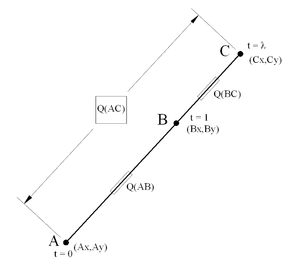
But the line can also be specified by two simultaneous equations in a parameter t, where t = 0 at point A and t = 1 at point B:
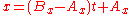and 
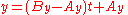
or, in terms of the original parameters:
and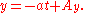 
If the point C is collinear with points A and B, there exists some value of t (for distinct points, not equal to 0 or 1), call it λ, for which these two equations are simultaneously satisfied at the coordinates of the point C, such that:
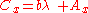and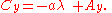 
Now, the quadrances of the three line segments are given by the squared differences of their coordinates, which can be expressed in terms of λ:
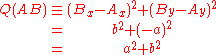
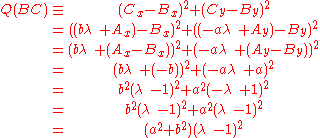
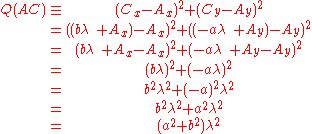
where use was made of the fact that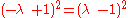
.
Substituting these quadrances into the equation to be proved:
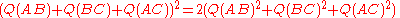
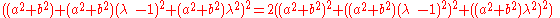
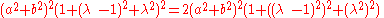
Now, if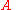
and 
represent distinct points, such that 
is not zero,
we may divide both sides by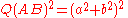
:
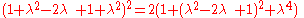
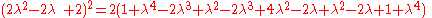
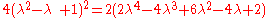
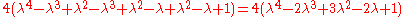
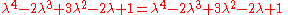
where Q3 is the quadrance between A1 and A2.
This is equivalent to the Pythagorean theorem
plus the inverse of the Pythagorean theorem.
There are many classical proofs of Pythagoras' theorem; this one is framed in the terms of rational trigonometry.
The spread of an angle is the square of its sine
. Given the triangle ABC with a spread of 1 between sides AB and AC,
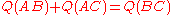
where Q is the "quadrance", i.e. the square of the distance.
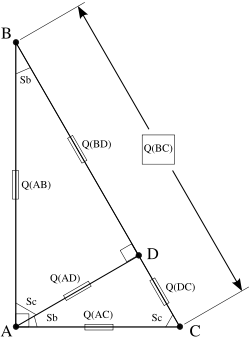Construct a line AD dividing the spread of 1, with the point D on line BC, and making a spread of 1 with DB and DC. The triangles ABC, DBA and DAC are similar (have the same spreads but not the same quadrances).
This leads to two equations in ratios, based on the spreads of the sides of the triangle:
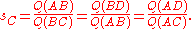
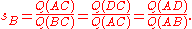
Now in general, the two spreads resulting from dividing a spread into two parts, as line AD does for spread CAB, do not add up to the original spread since spread is a non-linear function. So we first prove that dividing a spread of 1, results in two spreads that do add up to the original spread of 1.
For convenience, but with no loss of generality, we orient the lines intersecting with a spread of 1 to the coordinate axes, and label the dividing line with coordinates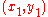
and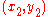 
. Then the two spreads are given by:
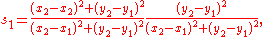
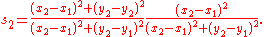
Hence:
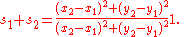
So that:
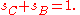
Using the first two ratios from the first set of equations, this can be rewritten:
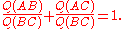
Multiplying both sides by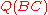
:
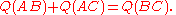
Q.E.D.
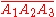with non zero quadrances:
This is the law of sines
, just squared.
,
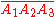This is analogous to the law of cosines
. It is called 'cross law' because
, the square of the cosine of the angle, is called the 'cross'.
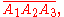
This corresponds (roughly) to the angle sum formulae for sine and cosine. If we know two of the spreads, this allows us to compute the third one. To do this we need to solve a second-degree equation, so it is sure more inconvenient than the analogue in classical trigonometry.
Given two lines whose equations are a1x + b1y = constant and a2x + b2y = constant, the spread between them is
. Other computations, (such as computing the quadrance of a line segment given the quadrance of two collinear line segments which compose it, or such as computing the spread of the sum of two angles with known spreads) do involve more computations than their classical analogues.
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
that eschews all transcendental function
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
s (such as sine and cosine) and all proportional measurements of angles. In place of angles, it characterizes the separation between lines by a quantity called the "spread", which is a rational function of their slopes
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
. In place of the classical transcendental functions, it introduces a number of "laws" between the lengths and spreads of lines bound by various geometric configurations, notably triangles.
Rational trigonometry was introduced by Prof. Norman J. Wildberger in his 2005 book Divine Proportions: Rational Trigonometry to Universal Geometry. The book is purposefully critical of traditional mathematics. One of the main claims the author makes is that the field of trigonometry is being taught and applied using choices in measurements and relations (such as angles and transcendental functions) that are arbitrarily complicated, are not necessary in order to reason about most concepts of the field, nor are they needed for most practical applications.
The author proposes new basic measurements on which to base the field itself and related applications (namely, the square of distance instead of the plain distance between two points, and the spread instead of the angle between two lines) and goes on to prove an array of theorems and laws to work with these measurements.
From there, the author rebuilds a great part of Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
on top of his new proposed measurements, using only rational equivalences, which allow him to avoid any assumptions about the underlying scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
. This is the Universal Geometry part of the book, where most classical findings of geometry are shown to be applicable to any field, including the field of rational numbers or finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
Wildberger holds a Ph.D. in mathematics from Yale University
Yale University
Yale University is a private, Ivy League university located in New Haven, Connecticut, United States. Founded in 1701 in the Colony of Connecticut, the university is the third-oldest institution of higher education in the United States...
, and taught at Stanford University
Stanford University
The Leland Stanford Junior University, commonly referred to as Stanford University or Stanford, is a private research university on an campus located near Palo Alto, California. It is situated in the northwestern Santa Clara Valley on the San Francisco Peninsula, approximately northwest of San...
from 1984 to 1986 and at the University of Toronto
University of Toronto
The University of Toronto is a public research university in Toronto, Ontario, Canada, situated on the grounds that surround Queen's Park. It was founded by royal charter in 1827 as King's College, the first institution of higher learning in Upper Canada...
from 1986 to 1989; he is currently an associate professor of mathematics at the University of New South Wales
University of New South Wales
The University of New South Wales , is a research-focused university based in Kensington, a suburb in Sydney, New South Wales, Australia...
, Australia
Australia
Australia , officially the Commonwealth of Australia, is a country in the Southern Hemisphere comprising the mainland of the Australian continent, the island of Tasmania, and numerous smaller islands in the Indian and Pacific Oceans. It is the world's sixth-largest country by total area...
.
Quadrance and spread
Instead of distance and angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
, rational trigonometry uses as its fundamental units quadrance (square of distance) and spread (square of sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
of angle). This choice of variables enables calculations to produce output results whose complexity matches that of the input data. For instance, in a typical trigonometry problem if rational numbers are assigned to all quadrances and spreads, then the calculated results will be rational numbers (or roots of rational numbers).
This rationality is obtained at the expense of linearity. Unlike the traditional distance and angle units, doubling or halving a quadrance or spread does not double or halve a length or a rotation. Similarly, the sum of two lengths or rotations is not the sum of their individual quadrances or spreads.
For distinction, Wildberger refers to the traditional trigonometry as classical trigonometry.
It is otherwise broadly based on Cartesian analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, with a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
defined as an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
(x, y) and a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
as a general linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
The mathematics of rational trigonometry is, applications aside, a special instance of the description of geometry in terms of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
(using rational methods such as dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s and quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s), but students who are first learning trigonometry are often not taught about the use of linear algebra in geometry. Changing this state of affairs is a stated aim of Wildberger's book (to paraphrase his comments).
Trigonometry over arbitrary fields
Rational trigonometry makes it possible to do trigonometry over any fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, not just the field of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
Quadrance
The quadrance is the square of the distance.Quadrance and distance are concerned with the separation of points. Quadrance differs from standard distance in that it squares the distance. Most immediately, this means that calculating the distance (or, more accurately, quadrance) between two points in 2-dimensional space is easier, as there is no need to find the square root of the sum of the squares of the differences in the x and y coordinates.
In the (x, y)-plane, the quadrance Q(A1, A2) for the points A1 and A2 is defined as
Spread
Suppose two lines, ℓ 1 and ℓ 2, intersect at the point A as shown at right. Choose a point B ≠ A on ℓ 1 and let C be the foot of the perpendicular from B to ℓ 2. Then the spread s is
Spread compared to angle
In rational trigonometry, spread is a fundamental concept, somewhat but not precisely corresponding to the concept in traditional geometry of angle. Spread describes a relationship between two linesLine (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, whereas angle describes a relationship between two rays emanating from a common point.
The spread is the square of the sine of the angle.
| Degree Degree (angle) A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians... | Radian Radian Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit... | Spread |
|---|---|---|
| 0 | 0 | 0 |
| 30 | (1/6)π | 1/4 |
| 45 | (1/4)π | 1/2 |
| 60 | (1/3)π | 3/4 |
| 90 | (1/2)π | 1 |
| 120 | (2/3)π | 3/4 |
| 135 | (3/4)π | 1/2 |
| 150 | (5/6)π | 1/4 |
| 180 | π | 0 |
Spread is not proportional to degrees or radians, and has a period of 180 degrees (π radians).
Laws of rational trigonometry
Wildberger states that there are five basic laws in rational trigonometry. He also states, correctly, that these laws can be verified using high-school level mathematics. Some are equivalent to standard trigonometrical formulae with the variables expressed as quadrance and spread.In the following five formulas, we have a triangle made of three points A1, A2, A3, . The spreads of the angles at those points are s1, s2, s3, , and Q1, Q2, Q3, are the quadrances of the triangle sides opposite A1, A2, and A3, respectively. As in classical trigonometry, if we know three of the six elements s1, s2, s3, , Q1, Q2, Q3, and these three are not the three s', then we can compute the other three.
Triple quad formula
The three points A1, A2, A3, are collinear if an only if:
This formula comes from applying is equivalent to using Heron's formula, the condition for collinearity being that the triangle formed by the three points has zero area.
It can either be proved by analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
(the preferred means within rational trigonometry) or derived from Heron's formula, using the condition for collinearity that the triangle formed by the three points has zero area.
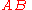has the general form:where the (non-unique) parameters a, b and c, can be expressed in terms of the coordinates of points A and B as:
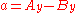
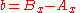
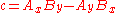
so that, everywhere on the line:
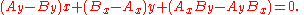
But the line can also be specified by two simultaneous equations in a parameter t, where t = 0 at point A and t = 1 at point B:
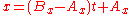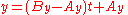
and or, in terms of the original parameters:
and 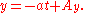If the point C is collinear with points A and B, there exists some value of t (for distinct points, not equal to 0 or 1), call it λ, for which these two equations are simultaneously satisfied at the coordinates of the point C, such that:
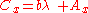and 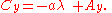Now, the quadrances of the three line segments are given by the squared differences of their coordinates, which can be expressed in terms of λ:
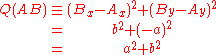
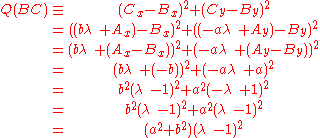
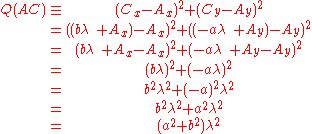
where use was made of the fact that
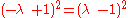.Substituting these quadrances into the equation to be proved:
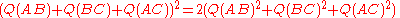
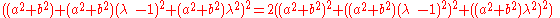
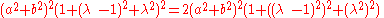
Now, if
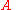and represent distinct points, such that is not zero,we may divide both sides by
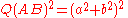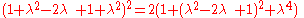
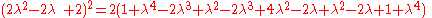
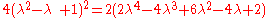
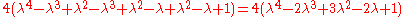
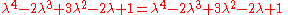
:Pythagoras' theorem
The lines A1A3 (of quadrance Q1) and A2A3 ((of quadrance Q2)) are perpendicular (their spread is 1) if and only if:
where Q3 is the quadrance between A1 and A2.
This is equivalent to the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
plus the inverse of the Pythagorean theorem.
There are many classical proofs of Pythagoras' theorem; this one is framed in the terms of rational trigonometry.
The spread of an angle is the square of its sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
. Given the triangle ABC with a spread of 1 between sides AB and AC,
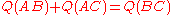
where Q is the "quadrance", i.e. the square of the distance.
This leads to two equations in ratios, based on the spreads of the sides of the triangle:
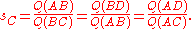
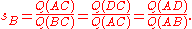
Now in general, the two spreads resulting from dividing a spread into two parts, as line AD does for spread CAB, do not add up to the original spread since spread is a non-linear function. So we first prove that dividing a spread of 1, results in two spreads that do add up to the original spread of 1.
For convenience, but with no loss of generality, we orient the lines intersecting with a spread of 1 to the coordinate axes, and label the dividing line with coordinates
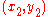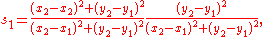
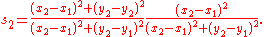
and . Then the two spreads are given by:Hence:
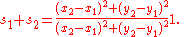
So that:
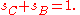
Using the first two ratios from the first set of equations, this can be rewritten:
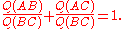
Multiplying both sides by
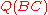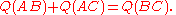
:Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
Spread law
For any triangle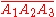 with non zero quadrances:
This is the law of sines
Law of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
, just squared.
Cross law
For any triangle,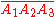
This is analogous to the law of cosines
Law of cosines
In trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
. It is called 'cross law' because
, the square of the cosine of the angle, is called the 'cross'.Triple spread formula
For any triangle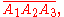
This corresponds (roughly) to the angle sum formulae for sine and cosine. If we know two of the spreads, this allows us to compute the third one. To do this we need to solve a second-degree equation, so it is sure more inconvenient than the analogue in classical trigonometry.
Calculating quadrance and spread
Given the coordinates of two points (x1, y1) and (x2, y2), the quadrance between them is
Given two lines whose equations are a1x + b1y = constant and a2x + b2y = constant, the spread between them is
Ease of calculation
Rational trigonometry makes some problems solvable with only addition, subtraction, multiplication, and division, with fewer uses of other functions such as square roots, sine, and cosine (compared with classical trigonometry). Such algorithms execute more efficiently on most computers, for problems such as solving trianglesSolution of triangles
In trigonometry, to solve a triangle is to find the three angles and the lengths of the three sides of the triangle when given some, but not all of that information...
. Other computations, (such as computing the quadrance of a line segment given the quadrance of two collinear line segments which compose it, or such as computing the spread of the sum of two angles with known spreads) do involve more computations than their classical analogues.