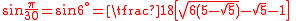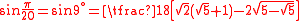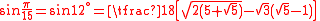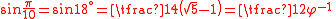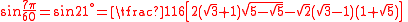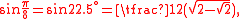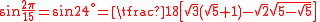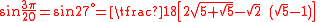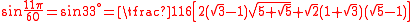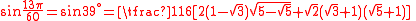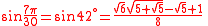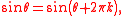Sine
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the sine function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
. In a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
.
Sine is usually listed first amongst the trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s.
Trigonometric functions are commonly defined as ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s of two sides of a right triangle containing the angle, and can equivalently be defined as the lengths of various line segments from a unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. More modern definitions express them as infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
or as solutions of certain differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, allowing their extension to arbitrary positive and negative values and even to complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
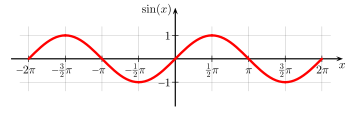
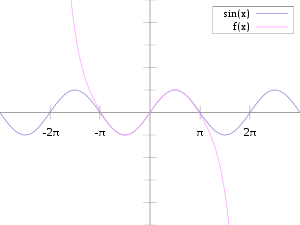
The sine function is commonly used to model periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
phenomena such as sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
and light waves, the position and velocity of harmonic oscillators, sunlight intensity and day length, and average temperature variations throughout the year.
The function sine can be traced to the jyā and koṭi-jyā
Jyā, koti-jyā and utkrama-jyā
Jyā, koti-jyā and utkrama-jyā are three trigonometric functions introduced by Indian astronomers and mathematicians. The earliest known Indian treatise containing references to these functions is Surya Siddhanta. These are functions of arcs of circles and not functions of angles. Jyā and...
functions used in Gupta period Indian astronomy (Aryabhatiya
Aryabhatiya
Āryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
, Surya Siddhanta
Surya Siddhanta
The Surya Siddhanta is one of the earliest siddhanta in archeo-astronomy of the Hindus by an unknown author. It describes the archeo-astronomy theories, principles and methods of the ancient Hindus. This siddhanta is supposed to be the knowledge that the Sun god gave to an Asura called Maya. Asuras...
), via translation from Sanskrit to Arabic and then from Arabic to Latin. The word "sine" comes from a Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
mistranslation of the Arabic jiba, which is a transliteration of the Sanskrit word for half the chord, jya-ardha.
Right-angled triangle definition
For any similar triangle the ratio of the length of the sides remains the same. For example, if the hypotenuse is twice as long, so are the other sides. Therefore respective trigonometric functions, depending only on the size of the angle, express those ratios: between the hypotenuse and the "opposite" side to an angle A in question (see illustration) in the case of sine function; or between the hypotenuse and the "adjacent" side (cosine) or between the "opposite" and the "adjacent" side (tangent), etc.To define the trigonometric functions for an acute angle A, start with any right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
that contains the angle A. The three sides of the triangle are named as follows:
- The hypotenuse is the side opposite the right angle, in this case side h. The hypotenuse is always the longest side of a right-angled triangle.
- The opposite side is the side opposite to the angle we are interested in (angle A), in this case side a.
- The adjacent side is the side that is in contact with (adjacent to) both the angle we are interested in (angle A) and the right angle, in this case side b.
In ordinary Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, according to the triangle postulate
Triangle postulate
In Euclidean geometry, the triangle postulate states that the sum of the angles of a triangle is two right angles. This postulate is equivalent to the parallel postulate...
the inside angles of every triangle total 180°
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
(π radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s). Therefore, in a right-angled triangle, the two non-right angles total 90° (π/2 radians), so each of these angles must be greater than 0° and less than 90°. The following definition applies to such angles.
The angle A (having measure α) is the angle between the hypotenuse and the adjacent line.
The sine of an angle is the ratio of the length of the opposite side
Cathetus
In a right triangle, the cathetus , commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called the periphrasis . The side opposite the right angle is the hypotenuse...
to the length of the hypotenuse. In our case

Note that this ratio does not depend on the size of the particular right triangle chosen, as long as it contains the angle A, since all such triangles are similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
.
Relation to slope
The trigonometric functions can be defined in terms of the rise, run, and slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of a line segment relative to some horizontal line.
- When the length of the line segment is 1, sine takes an angle and tells the rise
- Sine takes an angle and tells the rise per unit length of the line segment.
- Rise is equal to sin θ multiplied by the length of the line segment
In contrast, cosine is used for the telling the run from the angle; and tangent is used for telling the slope from the angle. Arctan is used for telling the angle from the slope.
The line segment is the equivalent of the hypotenuse in the right-triangle, and when it has a length of 1 it is also equivalent to the radius of the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
.
Relation to the unit circle
In trigonometryTrigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, a unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
.
Let a line through the origin, making an angle of θ with the positive half of the x-axis, intersect the unit circle. The x- and y-coordinates of this point of intersection are equal to cos θ and sin θ, respectively. The point's distance from the origin is always 1.
Unlike the definitions with the right triangle or slope, the angle can be extended to the full set of real arguments by using the unit circle. This can also be achieved by requiring certain symmetries and that sine be a periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
.

Identities
Exact identities (using radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s):
These apply for all values of
 .
.
Reciprocal
The reciprocalMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of sine is cosecant. i.e. the reciprocal of sin(A) is csc(A), or cosec(A). Cosecant gives the ratio of the length of the hypotenuse to the length of the opposite side:
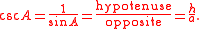
Inverse
The inverse functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of sine is arcsine (arcsin or asin) or inverse sine (sin). As sine is multivalued
Multivalued function
In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
, it is not an exact inverse function but a partial inverse function. For example, sin(0) = 0, but also sin(π) = 0, sin(2π) = 0 etc. It follows that the arcsine function is also multivalued: arcsin(0) = 0, but also arcsin(0) = π, arcsin(0) = 2π, etc. When only one value is desired, the function may be restricted to its principal branch
Principal branch
In mathematics, a principal branch is a function which selects one branch, or "slice", of a multi-valued function. Most often, this applies to functions defined on the complex plane: see branch cut....
. With this restriction, for each x in the domain the expression arcsin(x) will evaluate only to a single value, called its principal value
Principal value
In considering complex multiple-valued functions in complex analysis, the principal values of a function are the values along one chosen branch of that function, so it is single-valued.-Motivation:...
.

k is some integer:
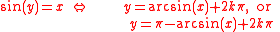
Arcsin satisfies:
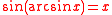
and
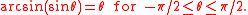
Calculus
For the sine function:
The derivative is:
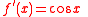
The antiderivative is:
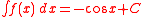
C denotes the constant of integration.
Other trigonomic functions
It is possible to express any trigonometric function in terms of any other (up to a plus or minus sign, or using the sign functionSign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
).
Sine in terms of the other common trigonometric functions:
| f θ | Using plus/minus (±) | Using sign function (sgn) | |||||
|---|---|---|---|---|---|---|---|
| f θ = | ± per Quadrant | f θ = | |||||
| I | II | III | IV | ||||
| cos |  |
 |
+ | + | - | - | 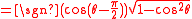 |
 |
 |
+ | - | - | + | 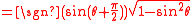 |
|
| cot | 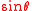 |
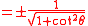 |
+ | + | - | - |  |
 |
 |
+ | - | - | + | 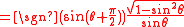 |
|
| tan | 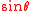 |
 |
+ | - | - | + |  |
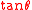 |
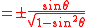 |
+ | - | - | + |  |
|
| sec | 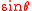 |
 |
+ | - | + | - | 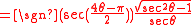 |
 |
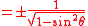 |
+ | - | - | + | 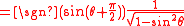 |
|
Note that for all equations which use plus/minus (±), the result is positive for angles in the first quadrant.
The basic relationship between the sine and the cosine can also be expressed as the Pythagorean trigonometric identity
Pythagorean trigonometric identity
The Pythagorean trigonometric identity is a trigonometric identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one the basic relations between the sine and cosine functions, from which all others may be derived.-Statement of...
:
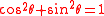
where sin2x means (sin(x))2.
Properties relating to the quadrants
Over the four quadrants of the sine function is as follows.| Quadrant | Degrees Degree (angle) A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians... |
Radians | Value | Sign Sign (mathematics) In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero... |
Monotony Monotonic function In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory.... |
Convexity Convex function In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set... |
|---|---|---|---|---|---|---|
| 1st Quadrant | 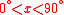 |
 |
 |
 |
increasing | concave |
| 2nd Quadrant |  |
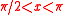 |
 |
 |
decreasing | concave |
| 3rd Quadrant | 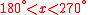 |
 |
 |
 |
decreasing | convex |
| 4th Quadrant | 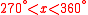 |
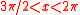 |
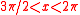 |
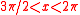 |
increasing | convex |
Points between the quadrants. k is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
.
| Degrees Degree (angle) A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians... |
Radians 0 ≤ x < 2π |
Radians | sin x | Point type |
|---|---|---|---|---|
 |
0 |  |
0 | Root, Inflection Inflection point In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa... |
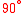 |
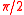 |
 |
1 | Maxima Maxima and minima In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the... |
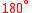 |
 |
 |
0 | Root, Inflection Inflection point In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa... |
 |
 |
 |
-1 | Minima |
For arguments outside of those in the table, get the value using the fact the sine function has a period of 360° (or 2π rad):
 , or use
, or use 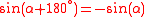 .
.For complement of sine, we have
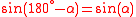
Series definition
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
, it can be shown that the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of sine is cosine and the derivative of cosine is the negative of sine.
Using the reflection from the calculated geometric derivation of the sine is with the 4n + k-th derivative at the point 0:

This gives the following Taylor series expansion at x = 0. One can then use the theory of Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
to show that the following identities hold for all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s x (where x is the angle in radians) :
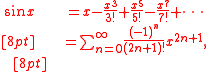
If x were expressed in degrees then the series would contain messy factors involving powers of π/180: if x is the number of degrees, the number of radians is y = πx /180, so

The series formulas for the sine and cosine are uniquely determined, up to the choice of unit for angles, by the requirements that
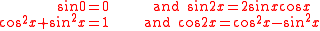
The radian is the unit that leads to the expansion with leading coefficient 1 for the sine and is determined by the additional requirement that
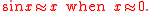
The coefficients for both the sine and cosine series may therefore be derived by substituting their expansions into the pythagorean and double angle identities, taking the leading coefficient for the sine to be 1, and matching the remaining coefficients.
In general, mathematically important relationships between the sine and cosine functions and the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
(see, for example, Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
) are substantially simplified when angles are expressed in radians, rather than in degrees, grads or other units. Therefore, in most branches of mathematics beyond practical geometry, angles are generally assumed to be expressed in radians.
A similar series is Gregory's series
Gregory's series
Gregory's series, also known as the Madhava-Gregory series or Leibniz's series, is a mathematical series that was discovered by the Indian mathematician Madhava of Sangamagrama...
for arctan, which is obtained by omitting the factorials in the denominator.
Continued fraction
The sine function can also be represented as a generalized continued fractionGeneralized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
:

The continued fraction representation expresses the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
values, both rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
and irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
, of the sine function.
Fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of the sine function because sin(0) = 0.
Law of sines
The law of sinesLaw of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
states that for an arbitrary triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
with sides a, b, and c and angles opposite those sides A, B and C:
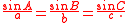
This is equivalent to the equality of the first three expressions below:

where R is the triangle's circumradius
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
.
It can be proven by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in triangulation
Triangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
, a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
Values

| x (angle) | sin x | |||
|---|---|---|---|---|
| Degrees | Radians | Grads | Exact | Decimal |
| 0° | 0 | 0g | 0 | 0 |
| 180° |  |
200g | ||
| 15° | 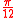 |
16g | 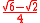 |
0.258819045102521 |
| 165° | 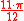 |
183g | ||
| 30° |  |
33g |  |
0.5 |
| 150° | 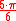 |
166g | ||
| 45° |  |
50g | 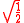 |
0.707106781186548 |
| 135° | 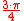 |
150g | ||
| 60° |  |
66g | 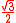 |
0.866025403784439 |
| 120° |  |
133g | ||
| 75° |  |
83g |  |
0.965925826289068 |
| 105° | 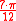 |
116g | ||
| 90° |  |
100g | 1 | 1 |
A memory aid (note it does not include 15° and 75°):
| x in degrees | 0° | 30° | 45° | 60° | 90° |
| x in radians | 0 | π/6 | π/4 | π/3 | π/2 |
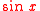 |
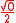 |
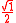 |
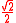 |
 |
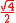 |
90 degree increments:
| x in degrees | 0° | 90° | 180° | 270° | 360° |
| x in radians | 0 | π/2 | π | 3π/2 | 2π |
 |
0 | 1 | 0 | ||
| 0 |
Other values not listed above:
For angles greater than 2π or less than −2π, simply continue to rotate around the circle; sine periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
with period 2π:
for any angle θ and any integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k.
The primitive period (the smallest positive period) of sine is a full circle, i.e. 2π radians or 360 degrees.
Relationship to complex numbers
Sine is used to determine the imaginary part of a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
given in polar coordinates (r,φ):
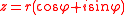
the imaginary part is:
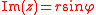
r and φ represent the magnitude and angle of the complex number respectively. i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. z is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
.
Although dealing with complex numbers, sine's parameter in this usage is still a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. Sine can also take a complex number as an argument.
Sine with a complex argument
The definition of the sine function for complex arguments z:-
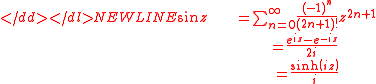
where i 2 = −1. This is an entire functionEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
. Also, for purely real x,
For purely imaginary numbers:
It is also sometimes useful to express the complex sine function in terms of the real and imaginary parts of its argument:
-
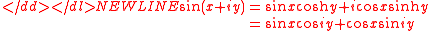
Usage of complex sine
sin z is found in the functional equationFunctional equationIn mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
for the Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
,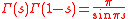 .
.
Which in turn is found in the functional equationFunctional equationIn mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
for the Riemann zeta-function,
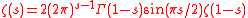
As a holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
, sin z is a 2D solution of Laplace's equationLaplace's equationIn mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
:
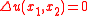
Complex graphs
Sine function in the complex plane real component imaginary component magnitude
Sin in the complex plane real component imaginary component magnitude
History
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period.
The chordChord (geometry)A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
function was discovered by HipparchusHipparchusHipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
of NicaeaIznikİznik is a city in Turkey which is primarily known as the site of the First and Second Councils of Nicaea, the first and seventh Ecumenical councils in the early history of the Church, the Nicene Creed, and as the capital city of the Empire of Nicaea...
(180–125 BC) and PtolemyPtolemyClaudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
of Roman Egypt (90–165 AD).
The function sine (and cosine) can be traced to the jyā and koṭi-jyāJyā, koti-jyā and utkrama-jyāJyā, koti-jyā and utkrama-jyā are three trigonometric functions introduced by Indian astronomers and mathematicians. The earliest known Indian treatise containing references to these functions is Surya Siddhanta. These are functions of arcs of circles and not functions of angles. Jyā and...
functions used in Gupta period Indian astronomy (AryabhatiyaAryabhatiyaĀryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
, Surya SiddhantaSurya SiddhantaThe Surya Siddhanta is one of the earliest siddhanta in archeo-astronomy of the Hindus by an unknown author. It describes the archeo-astronomy theories, principles and methods of the ancient Hindus. This siddhanta is supposed to be the knowledge that the Sun god gave to an Asura called Maya. Asuras...
), via translation from Sanskrit to Arabic and then from Arabic to Latin.
The first published use of the abbreviations 'sin', 'cos', and 'tan' is by the 16th century French mathematician Albert GirardAlbert GirardAlbert Girard was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and gave the inductive definition for the Fibonacci numbers....
; these were further promulgated by Euler (see below). The Opus palatinum de triangulis of Georg Joachim RheticusGeorg Joachim RheticusGeorg Joachim von Lauchen, also known as Rheticus , was a mathematician, cartographer, navigational-instrument maker, medical practitioner, and teacher. He is perhaps best known for his trigonometric tables and as Nicolaus Copernicus's sole pupil...
, a student of Copernicus, was probably the first in Europe to define trigonometric functions directly in terms of right triangles instead of circles, with tables for all six trigonometric functions; this work was finished by Rheticus' student Valentin Otho in 1596.
In a paper published in 1682, LeibnizGottfried LeibnizGottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
proved that sin x is not an algebraic functionAlgebraic functionIn mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
of x. Roger CotesRoger CotesRoger Cotes FRS was an English mathematician, known for working closely with Isaac Newton by proofreading the second edition of his famous book, the Principia, before publication. He also invented the quadrature formulas known as Newton–Cotes formulas and first introduced what is known today as...
computed the derivative of sine in his Harmonia Mensurarum (1722). Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
's Introductio in analysin infinitorum (1748) was mostly responsible for establishing the analytic treatment of trigonometric functions in Europe, also defining them as infinite series and presenting "Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
", as well as the near-modern abbreviations sin., cos., tang., cot., sec., and cosec.
Etymology
EtymologicallyEtymologyEtymology is the study of the history of words, their origins, and how their form and meaning have changed over time.For languages with a long written history, etymologists make use of texts in these languages and texts about the languages to gather knowledge about how words were used during...
, the word sine derives from the SanskritSanskritSanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
word for chord, jiva*(jya being its more popular synonym). This was transliteratedTransliterationTransliteration is a subset of the science of hermeneutics. It is a form of translation, and is the practice of converting a text from one script into another...
in ArabicArabic languageArabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
as jiba جــيــب , abbreviated jb جــــب . Since Arabic is written without short vowels, "jb" was interpreted as the word jaib جــيــب , which means "bosom", when the Arabic text was translated in the 12th century into Latin by Gerard of CremonaGerard of CremonaGerard of Cremona was an Italian translator of Arabic scientific works found in the abandoned Arab libraries of Toledo, Spain....
. The translator used the Latin equivalent for "bosom", sinus (which means "bosom" or "bay" or "fold") The English form sine was introduced in the 1590s.
Software implementations
The sin function, along with other trigonometric functions, is widely available across programming languages and platforms. Some CPU architectures have a built-in instruction for sin, including the Intel x86 FPU. In programming languages, sin is usually either a built in function or found within the language's standard math library. There is no standard algorithm for calculating sin. IEEE 754-2008, the most widely-used standard for floating-point computation, says nothing on the topic of calculating trigonometric functions such as sin. Algorithms for calculating sin may be balanced for such constraints as speed, accuracy, portability, or range of input values accepted. This can lead to very different results for different algorithms in special circumstances, such as for very large inputs, e.g. sin(10).
A once common programming optimization, used especially in 3D graphics, was to pre-calculate a table of sin values, for example a value per degree. This allowed results to be looked up from a table rather than being calculated in real time. With modern CPU architectures this method typically offers no advantage.
See also
- Sine waveSine waveThe sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
- Trigonometric functions
- Sinusoidal modelSinusoidal modelIn statistics, signal processing, and time series analysis, a sinusoidal model to approximate a sequence Yi is:Y_i = C + \alpha\sin + E_i...
- Discrete sine transformDiscrete sine transformIn mathematics, the discrete sine transform is a Fourier-related transform similar to the discrete Fourier transform , but using a purely real matrix...
- Law of sinesLaw of sinesIn trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
- Sine and cosine transformsSine and cosine transformsIn mathematics, the Fourier sine and cosine transforms are special cases of thecontinuous Fourier transform, arising naturally when attempting to transform odd and even functions, respectively.The general Fourier transform is defined as:...
- Sine quadrant
- Aryabhata's sine tableĀryabhaṭa's sine tableĀryabhaṭa's sine table is a set of twenty-four of numbers given in the astronomical treatise Āryabhaṭiya composed by the fifth century Indian mathematician and astronomer Āryabhaṭa , for the computation of the half-chords of certain set of arcs of a circle...
- Madhava's sine tableMadhava's sine tableMadhava's sine table is the table of trigonometric sines of various angles constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama. The table lists the trigonometric sines of the twenty-four angles 3.75°, 7.50°, 11.25°, ... , and 90.00°...
- Madhava seriesMadhava seriesIn mathematics, a Madhava series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by Sangamagrama Madhava the founder of the Kerala school of astronomy and mathematics...
- Bhaskara I's sine approximation formulaBhaskara I's sine approximation formulaIn mathematics, a certain rational expression in one variable for the computation of the approximate values of the trigonometric sines discovered by Bhaskara I , a seventh century Indian mathematician, is known as Bhaskara I's sine approximation formula.This formula is given in his treatise...
- Hyperbolic functionHyperbolic functionIn mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
- List of trigonometric identities
- Proofs of trigonometric identitiesProofs of trigonometric identitiesProofs of trigonometric identities are used to show relations between trigonometric functions. This article will list trigonometric identities and prove them.-Definitions:Referring to the diagram at the right, the six trigonometric functions of θ are:...
- Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
- Polar sinePolar sineIn mathematics, the polar sine of a vertex angle of a polytope is defined as follows. Let v1, ..., vn, n ≥ 2, be non-zero vectors from the vertex in the directions of the edges...
— a generalization to vertex angles - Optical sine theoremOptical sine theoremIn optics, the optical sine theorem states that the products of the index, height, and sine of the slope angle of a ray in object space and its corresponding ray in image space are equal. That is:...
- Generalized trigonometryGeneralized trigonometryOrdinary trigonometry studies triangles in the euclidean plane R2. There are a number of ways of defining the ordinary euclidean geometric trigonometric functions on real numbers: right-angled triangle definitions, unit-circle definitions, series definitions, definitions via differential equations,...
- Sine–Gordon equation
- Sine wave
-