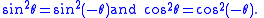Pythagorean trigonometric identity
Encyclopedia
The Pythagorean trigonometric identity is a trigonometric identity expressing the Pythagorean theorem
in terms of trigonometric function
s. Along with the sum-of-angles formulae, it is one the basic relations between the sine
and cosine functions, from which all others may be derived.
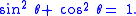
(Note that means . This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity.
If the length of the hypotenuse of a right triangle
is 1, then the lengths of the legs are the sine
and cosine of one of the angles. Therefore, this trigonometric identity follows from the Pythagorean theorem
.
The elementary definitions of the sine and cosine functions in terms of the sides of a right triangle are:


The Pythagorean identity follows by squaring both definitions above, and adding; the left-hand side of the identity then becomes

which by the Pythagorean theorem is equal to 1. Note, however, that this definition is valid only for angles between 0 and π/2 radians (not inclusive) and therefore this argument does not prove the identity for all angles. Values of 0 and π/2 are trivially proven by direct evaluation of sin and cos at those angles.
To complete the proof, the identities found at Trigonometric symmetry, shifts, and periodicity may be employed. By the periodicity identities we can say if the formula is true for then it is true for all real θ. Next we prove the range to do this we let t will now be in the range We can then make use of squared versions of some basic shift identities (squaring conveniently removes the minus signs):
All that remains is to prove it for this can be done by squaring the symmetry identities to get

and
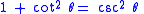
are also called Pythagorean trigonometric identities. If one leg of a right triangle has length 1, then the tangent of the angle adjacent to that leg is the length of the other leg, and the secant of the angle is the length of the hypotenuse.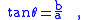
and: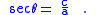
In this way, this trigonometric identity involving the tangent and the secant follows from the Pythagorean theorem. The angle opposite the leg of length 1 (this angle can be labeled φ = π/2 − θ) has cotangent equal to the length of the other leg, and cosecant equal to the length of the hypotenuse. In that way, this trigonometric identity involving the cotangent and the cosecant also follows from the Pythagorean theorem.
Another way of thinking about the other identities is to derive them from the original identity. The following table shows how this is done by dividing each element of the original Pythagorean Identity by a common divisor.
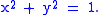
Given an angle θ, there is a unique point P on the unit circle at an angle θ from the x-axis, and the x- and y-coordinates of P are:
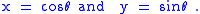
Consequently, from the equation for the unit circle: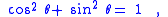
the Pythagorean identity.
In the figure, the point P has a negative x-coordinate, and is appropriately given by x = cosθ, which is a negative number: cosθ = −cos(π−θ ). Point P has a positive y-coordinate, and sinθ = sin(π−θ ) > 0. As θ increases from zero to the full circle θ = 2π, the sine and cosine change signs in the various quadrants to keep x and y with the correct signs. The figure shows how the sign of the sine function varies as the angle changes quadrant.
Because the x- and y-axes are perpendicular, this Pythagorean identity is actually equivalent to the Pythagorean theorem for triangles with hypotenuse of length 1 (which is in turn equivalent to the full Pythagorean theorem by applying a similar-triangles argument). See unit circle
for a short explanation.
s):
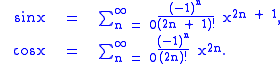
Using the formal multiplication law for power series at Multiplication and division of power series (suitably modified to account for the form of the series here) we obtain
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
in terms of trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s. Along with the sum-of-angles formulae, it is one the basic relations between the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and cosine functions, from which all others may be derived.
Statement of the identity
Mathematically, the Pythagorean identity states: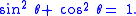
(Note that means . This relation between sine and cosine is sometimes called the fundamental Pythagorean trigonometric identity.
If the length of the hypotenuse of a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
is 1, then the lengths of the legs are the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and cosine of one of the angles. Therefore, this trigonometric identity follows from the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.
Proofs and their relationships to the Pythagorean theorem
Proof based on right-angle triangles
Any similar triangles have the property that if we select the same angle in all them, the ratio of the two sides defining the angle is the same regardless of which similar triangle is selected, regardless of its actual size: the ratios depend upon the three angles, not the lengths of the sides. Thus for either of the similar right triangles in the figure, the ratio of its horizontal side to its hypotenuse is the same, namely cos θ.The elementary definitions of the sine and cosine functions in terms of the sides of a right triangle are:


The Pythagorean identity follows by squaring both definitions above, and adding; the left-hand side of the identity then becomes

which by the Pythagorean theorem is equal to 1. Note, however, that this definition is valid only for angles between 0 and π/2 radians (not inclusive) and therefore this argument does not prove the identity for all angles. Values of 0 and π/2 are trivially proven by direct evaluation of sin and cos at those angles.
To complete the proof, the identities found at Trigonometric symmetry, shifts, and periodicity may be employed. By the periodicity identities we can say if the formula is true for then it is true for all real θ. Next we prove the range to do this we let t will now be in the range We can then make use of squared versions of some basic shift identities (squaring conveniently removes the minus signs):
All that remains is to prove it for this can be done by squaring the symmetry identities to get
Related identities
The identities
and
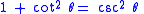
are also called Pythagorean trigonometric identities. If one leg of a right triangle has length 1, then the tangent of the angle adjacent to that leg is the length of the other leg, and the secant of the angle is the length of the hypotenuse.
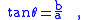
and:
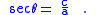
In this way, this trigonometric identity involving the tangent and the secant follows from the Pythagorean theorem. The angle opposite the leg of length 1 (this angle can be labeled φ = π/2 − θ) has cotangent equal to the length of the other leg, and cosecant equal to the length of the hypotenuse. In that way, this trigonometric identity involving the cotangent and the cosecant also follows from the Pythagorean theorem.
Tabulation of derivations
Another way of thinking about the other identities is to derive them from the original identity. The following table shows how this is done by dividing each element of the original Pythagorean Identity by a common divisor.
| Original Identity | Divisor | Divisor Equation | Derived Identity | Derived Identity (Alternate) |
|---|---|---|---|---|
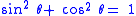 |
||||
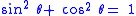 |
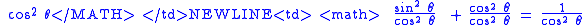 |
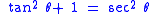 |
 |
|
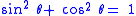 |
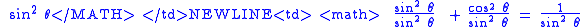 |
 |
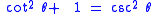 |
|
Proof using the unit circle
The unit circle centered at the origin in the Euclidean plane is defined by the equation: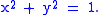
Given an angle θ, there is a unique point P on the unit circle at an angle θ from the x-axis, and the x- and y-coordinates of P are:
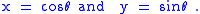
Consequently, from the equation for the unit circle:
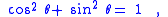
the Pythagorean identity.
In the figure, the point P has a negative x-coordinate, and is appropriately given by x = cosθ, which is a negative number: cosθ = −cos(π−θ ). Point P has a positive y-coordinate, and sinθ = sin(π−θ ) > 0. As θ increases from zero to the full circle θ = 2π, the sine and cosine change signs in the various quadrants to keep x and y with the correct signs. The figure shows how the sign of the sine function varies as the angle changes quadrant.
Because the x- and y-axes are perpendicular, this Pythagorean identity is actually equivalent to the Pythagorean theorem for triangles with hypotenuse of length 1 (which is in turn equivalent to the full Pythagorean theorem by applying a similar-triangles argument). See unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
for a short explanation.
Proof using power series
The trigonometric functions may also be defined using power series, namely (for x an angle measured in radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s):
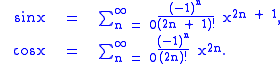
Using the formal multiplication law for power series at Multiplication and division of power series (suitably modified to account for the form of the series here) we obtain
-
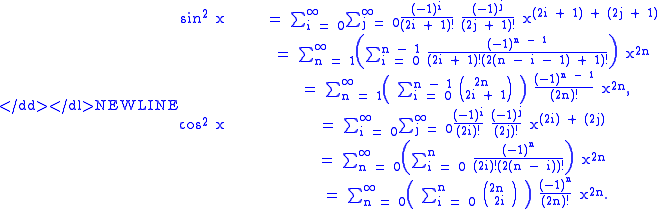
Note that in the expression for sin2, n must be at least 1, while in the expression for cos2, the constant termConstant termIn mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
is equal to 1. The remaining terms of their sum are (with common factors removed)
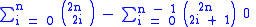
by the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. Consequently,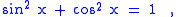
which is the Pythagorean trigonometric identity.
The Pythagorean theorem is not closely related to the Pythagorean identity when the trigonometric functions are defined in this way; instead, in combination with the theorem, the identity now shows that these power series parameterize the unit circle, which we used in the previous section. Note that this definition actually constructs the sin and cos functions in a rigorous fashion and proves that they are differentiable, so that in fact it subsumes the previous two.
Proof using the differential equation
Sine and Cosine can be defined as the two solutions to the differential equation:
satisfying respectively y(0) = 0, y′(0) = 1 and y(0) = 1, y′(0) = 0. It follows from the theory of ordinary differential equationOrdinary differential equationIn mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s that the first solution, sine, has the second, cosine, as its derivative, and it follows from this that the derivative of cosine is the negative of the sine. The identity is equivalent to the assertion that the function
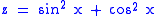
is constant and equal to 1. Differentiating using the chain ruleChain ruleIn calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
gives:
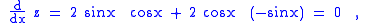
so z is constant. A calculation confirms that z(0) = 1, and z is a constant so z = 1 for all x, so the Pythagorean identity is established.
A similar proof can be completed using power series as above to establish that the sine has as its derivative the cosine, and the cosine has as its derivative the negative sine. In fact, the definitions by ordinary differential equation and by power series lead to similar derivations of most identities.
This proof of the identity has no direct connection with Euclid's demonstration of the Pythagorean theorem.
See also
- Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
- Trigonometric identity
- Unit circleUnit circleIn mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
- Power series
- Differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
External links
-