
Sine and cosine transforms
Encyclopedia
In mathematics
, the Fourier sine and cosine transforms are special cases of the
continuous Fourier transform
, arising naturally when attempting to transform odd and even functions
, respectively.
The general Fourier transform
is defined as:
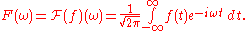
Expanding the integrand by means of Euler's formula
results in:
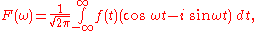
which may be written as the sum
of two integral
s:
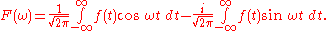
The Fourier sine transform and Fourier cosine transform are derived from this.
about the origin
(i.e. -∞ to +∞), the first integral must vanish to zero, and the second may be simplified to give:
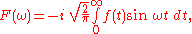
which is the Fourier sine transform for odd f(t). It is clear that the transformed function F(ω) is also an odd function, and a similar analysis of the general Inverse Fourier transform yields a second sine transform, namely:
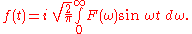
The numerical factors in the transforms are defined uniquely only by their product, as discussed for general continuous Fourier transforms. For this reason the imaginary unit
s i and -i can be omitted, with the more commonly seen forms of the Fourier sine transforms being:
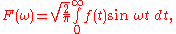
and
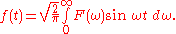
f(t)cosωt is also even whilst the product f(t)sinωt is an odd function. Since the integral is being computed over an interval symmetric about the origin (i.e. -∞ to +∞), the second integral must vanish to zero, and the first may be simplified to give:
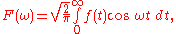
which is the Fourier cosine transform for even f(t). It is clear that the transformed function F(ω) is also an even function, and a similar analysis of the general inverse Fourier transform yields a second cosine transform, namely:
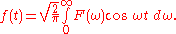
The numerical factors in the transforms are defined uniquely only by their product, as discussed for general continuous Fourier transforms.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fourier sine and cosine transforms are special cases of the
continuous Fourier transform
Continuous Fourier transform
The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
, arising naturally when attempting to transform odd and even functions
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
, respectively.
The general Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is defined as:
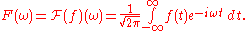
Expanding the integrand by means of Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
results in:
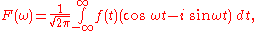
which may be written as the sum
SUM
SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of two integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s:
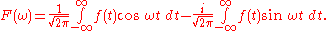
The Fourier sine transform and Fourier cosine transform are derived from this.
Fourier sine transform
The Fourier sine transform is a special case of the continuous Fourier transform, arising naturally when attempting to transform an odd function. From the general Fourier transform noted above, if f(t) is assumed to be an odd function, the product f(t)cosωt is also odd whilst the product f(t)sinωt is an even function. Since the integral is being computed over an interval symmetricSymmetry in mathematics
Symmetry occurs not only in geometry, but also in other branches of mathematics. It is actually the same as invariance: the property that something does not change under a set of transformations....
about the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
(i.e. -∞ to +∞), the first integral must vanish to zero, and the second may be simplified to give:
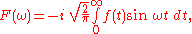
which is the Fourier sine transform for odd f(t). It is clear that the transformed function F(ω) is also an odd function, and a similar analysis of the general Inverse Fourier transform yields a second sine transform, namely:
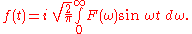
The numerical factors in the transforms are defined uniquely only by their product, as discussed for general continuous Fourier transforms. For this reason the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
s i and -i can be omitted, with the more commonly seen forms of the Fourier sine transforms being:
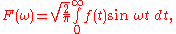
and
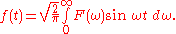
Fourier cosine transform
The Fourier cosine transform is a special case of the continuous Fourier transform, arising naturally when attempting to transform an even function. From the general Fourier transform noted above, if f(t) is assumed to be an even function, the productProduct (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
f(t)cosωt is also even whilst the product f(t)sinωt is an odd function. Since the integral is being computed over an interval symmetric about the origin (i.e. -∞ to +∞), the second integral must vanish to zero, and the first may be simplified to give:
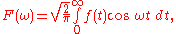
which is the Fourier cosine transform for even f(t). It is clear that the transformed function F(ω) is also an even function, and a similar analysis of the general inverse Fourier transform yields a second cosine transform, namely:
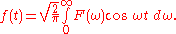
The numerical factors in the transforms are defined uniquely only by their product, as discussed for general continuous Fourier transforms.

