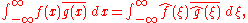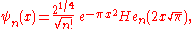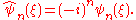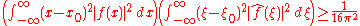Continuous Fourier transform
Encyclopedia
The Fourier transform is a mathematical operation that decomposes a function
into its constituent frequencies, known as a frequency spectrum
. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes (and phase
) of the individual notes that make it up. The composite waveform depends on time
, and therefore is called the time domain
representation. The frequency spectrum is a function of frequency and is called the frequency domain
representation. Each value of the function is a complex number (called complex amplitude) that encodes both a magnitude and phase component. The term "Fourier transform" refers to both the transform operation and to the complex-valued function it produces.
In the case of a periodic function
, like the musical chord, the Fourier transform can be simplified to the calculation of a discrete set of complex amplitudes, called Fourier series
coefficients. Also, when a time-domain function is sampled
to facilitate storage and/or computer-processing, it is still possible to recreate a version of the original Fourier transform according to the Poisson summation formula
, also known as discrete-time Fourier transform
. These topics are addressed in separate articles. For an overview of those and other related operations, refer to Fourier analysis or List of Fourier-related transforms.
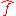 of an integrable
of an integrable
function . This article will use the definition: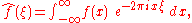 for every real number
for every real number
ξ.
When the independent variable x represents time (with SI
unit of second
s), the transform variable ξ represents frequency
(in hertz
). Under suitable conditions, ƒ can be reconstructed from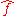 by the inverse transform:
by the inverse transform:
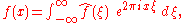 for every real number x.
for every real number x.
For other common conventions and notations, including using the angular frequency
ω
instead of the frequency
ξ, see Other conventions and Other notations below. The Fourier transform on Euclidean space is treated separately, in which the variable x often represents position and ξ momentum.
. In the study of Fourier series, complicated functions are written as the sum of simple waves mathematically represented by sine
s and cosines. Due to the properties of sine and cosine it is possible to recover the amount of each wave in the sum by an integral. In many cases it is desirable to use Euler's formula
, which states that e2πiθ = cos 2πθ + i sin 2πθ, to write Fourier series in terms of the basic waves e2πiθ. This has the advantage of simplifying many of the formulas involved and providing a formulation for Fourier series that more closely resembles the definition followed in this article. This passage from sines and cosines to complex exponentials makes it necessary for the Fourier coefficients to be complex valued. The usual interpretation of this complex number is that it gives both the amplitude
(or size) of the wave present in the function and the phase
(or the initial angle) of the wave. This passage also introduces the need for negative "frequencies". If θ were measured in seconds then the waves e2πiθ and e−2πiθ would both complete one cycle per second, but they represent different frequencies in the Fourier transform. Hence, frequency no longer measures the number of cycles per unit time, but is closely related.
There is a close connection between the definition of Fourier series and the Fourier transform for functions ƒ which are zero outside of an interval. For such a function we can calculate its Fourier series on any interval that includes the interval where ƒ is not identically zero. The Fourier transform is also defined for such a function. As we increase the length of the interval on which we calculate the Fourier series, then the Fourier series coefficients begin to look like the Fourier transform and the sum of the Fourier series of ƒ begins to look like the inverse Fourier transform. To explain this more precisely, suppose that T is large enough so that the interval [−T/2,T/2] contains the interval on which ƒ is not identically zero. Then the n-th series coefficient cn is given by:
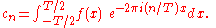
Comparing this to the definition of the Fourier transform it follows that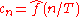 since ƒ(x) is zero outside [−T/2,T/2]. Thus the Fourier coefficients are just the values of the Fourier transform sampled on a grid of width 1/T. As T increases the Fourier coefficients more closely represent the Fourier transform of the function.
since ƒ(x) is zero outside [−T/2,T/2]. Thus the Fourier coefficients are just the values of the Fourier transform sampled on a grid of width 1/T. As T increases the Fourier coefficients more closely represent the Fourier transform of the function.
Under appropriate conditions the sum of the Fourier series of ƒ will equal the function ƒ. In other words ƒ can be written:
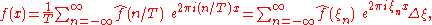
where the last sum is simply the first sum rewritten using the definitions ξn = n/T, and Δξ = (n + 1)/T − n/T = 1/T.
This second sum is a Riemann sum
, and so by letting T → ∞ it will converge to the integral for the inverse Fourier transform given in the definition section. Under suitable conditions this argument may be made precise .
In the study of Fourier series the numbers cn could be thought of as the "amount" of the wave in the Fourier series of ƒ. Similarly, as seen above, the Fourier transform can be thought of as a function that measures how much of each individual frequency is present in our function ƒ, and we can recombine these waves by using an integral (or "continuous sum") to reproduce the original function.
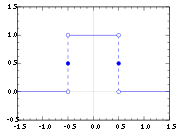
The following images provide a visual illustration of how the Fourier transform measures whether a frequency is present in a particular function. The function depicted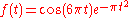 oscillates at 3 hertz (if t measures seconds) and tends quickly to 0. This function was specially chosen to have a real Fourier transform which can easily be plotted. The first image contains its graph. In order to calculate
oscillates at 3 hertz (if t measures seconds) and tends quickly to 0. This function was specially chosen to have a real Fourier transform which can easily be plotted. The first image contains its graph. In order to calculate 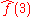
we must integrate e−2πi(3t)ƒ(t). The second image shows the plot of the real and imaginary parts of this function. The real part of the integrand is almost always positive, this is because when ƒ(t) is negative, then the real part of e−2πi(3t) is negative as well. Because they oscillate at the same rate, when ƒ(t) is positive, so is the real part of e−2πi(3t). The result is that when you integrate the real part of the integrand you get a relatively large number (in this case 0.5). On the other hand, when you try to measure a frequency that is not present, as in the case when we look at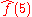 , the integrand oscillates enough so that the integral is very small. The general situation may be a bit more complicated than this, but this in spirit is how the Fourier transform measures how much of an individual frequency is present in a function ƒ(t).
, the integrand oscillates enough so that the integral is very small. The general situation may be a bit more complicated than this, but this in spirit is how the Fourier transform measures how much of an individual frequency is present in a function ƒ(t).
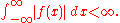
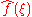 ,
, 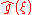 , and
, and  respectively. The Fourier transform has the following basic properties .
respectively. The Fourier transform has the following basic properties .
Linearity
Translation
Modulation
Scaling
Conjugation
Duality
Convolution
.svg.png) The Fourier transform may be defined in some cases for non-integrable functions, but the Fourier transforms of integrable functions have several strong properties.
The Fourier transform may be defined in some cases for non-integrable functions, but the Fourier transforms of integrable functions have several strong properties.
The Fourier transform of any integrable function ƒ is uniformly continuous and
of any integrable function ƒ is uniformly continuous and  . By the Riemann–Lebesgue lemma ,
. By the Riemann–Lebesgue lemma ,
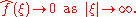
Furthermore,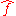 is bounded and continuous, but need not be integrable. For example, the Fourier transform of the rectangular function, which is integrable, is the sinc function, which is not Lebesgue integrable, because its improper integral
is bounded and continuous, but need not be integrable. For example, the Fourier transform of the rectangular function, which is integrable, is the sinc function, which is not Lebesgue integrable, because its improper integral
s behave analogously to the alternating harmonic series, in converging to a sum without being absolutely convergent.
It is not generally possible to write the inverse transform as a Lebesgue integral. However, when both ƒ and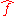 are integrable, the inverse equality
are integrable, the inverse equality
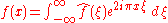
holds almost everywhere
. That is, the Fourier transform is injective on L1(R)
.
(But if ƒ is continuous, then equality holds for every x.)
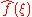 and
and 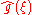 be their Fourier transforms. If f(x) and g(x) are also square-integrable, then we have Parseval's theorem
be their Fourier transforms. If f(x) and g(x) are also square-integrable, then we have Parseval's theorem
:
where the bar denotes complex conjugation.
The Plancherel theorem
, which is equivalent to Parseval's theorem
, states :
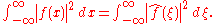
The Plancherel theorem makes it possible to define the Fourier transform for functions in L2(R), as described in Generalizations below. The Plancherel theorem has the interpretation in the sciences that the Fourier transform preserves the energy of the original quantity. It should be noted that depending on the author either of these theorems might be referred to as the Plancherel theorem or as Parseval's theorem.
See Pontryagin duality
for a general formulation of this concept in the context of locally compact abelian groups.
and multiplication of functions. If ƒ(x) and g(x) are integrable functions with Fourier transforms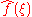 and
and 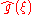 respectively, then the Fourier transform of the convolution is given by the product of the Fourier transforms
respectively, then the Fourier transform of the convolution is given by the product of the Fourier transforms 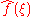 and
and 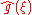 (under other conventions for the definition of the Fourier transform a constant factor may appear).
(under other conventions for the definition of the Fourier transform a constant factor may appear).
This means that if:
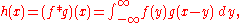
where ∗ denotes the convolution operation, then:
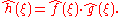
In linear time invariant (LTI) system theory
, it is common to interpret g(x) as the impulse response
of an LTI system with input ƒ(x) and output h(x), since substituting the unit impulse
for ƒ(x) yields h(x) = g(x). In this case,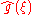 represents the frequency response
represents the frequency response
of the system.
Conversely, if ƒ(x) can be decomposed as the product of two square integrable functions p(x) and q(x), then the Fourier transform of ƒ(x) is given by the convolution of the respective Fourier transforms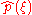 and
and 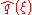 .
.
of ƒ(x) and g(x):
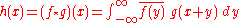
then the Fourier transform of h(x) is:
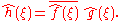
As a special case, the autocorrelation
of function ƒ(x) is: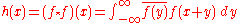
for which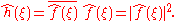
is given by the Hermite functions
where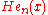 are the "probabilist's" Hermite polynomials, defined by Hen(x) = (−1)nexp(x2/2) Dn exp(−x2/2). Under this convention for the Fourier transform, we have that
are the "probabilist's" Hermite polynomials, defined by Hen(x) = (−1)nexp(x2/2) Dn exp(−x2/2). Under this convention for the Fourier transform, we have that
In other words, the Hermite functions form a complete orthonormal system of eigenfunctions for the Fourier transform on L2(R) . However, this choice of eigenfunctions is not unique. There are only four different eigenvalues of the Fourier transform (±1 and ±i) and any linear combination of eigenfunctions with the same eigenvalue gives another eigenfunction. As a consequence of this, it is possible to decompose L2(R) as a direct sum of four spaces H0, H1, H2, and H3 where the Fourier transform acts on Hek simply by multiplication by ik. This approach to define the Fourier transform is due to N. Wiener . The choice of Hermite functions is convenient because they are exponentially localized in both frequency and time domains, and thus give rise to the fractional Fourier transform
used in time-frequency analysis .
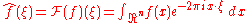
where x and ξ are n-dimensional vectors, and is the dot product
of the vectors. The dot product is sometimes written as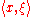 .
.
All of the basic properties listed above hold for the n-dimensional Fourier transform, as do Plancherel's and Parseval's theorem. When the function is integrable, the Fourier transform is still uniformly continuous and the Riemann–Lebesgue lemma holds.
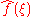 must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we "squeeze" a function in x, its Fourier transform "stretches out" in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.
must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we "squeeze" a function in x, its Fourier transform "stretches out" in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.
The trade-off between the compaction of a function and its Fourier transform can be formalized in the form of an uncertainty principle
by viewing a function and its Fourier transform as conjugate variables
with respect to the symplectic form on the time–frequency domain: from the point of view of the linear canonical transformation
, the Fourier transform is rotation by 90° in the time–frequency domain, and preserves the symplectic form
.
Suppose ƒ(x) is an integrable and square-integrable function. Without loss of generality, assume that ƒ(x) is normalized:
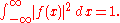
It follows from the Plancherel theorem
that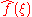 is also normalized.
is also normalized.
The spread around x = 0 may be measured by the dispersion about zero defined by
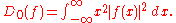
In probability terms, this is the second moment
of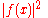 about zero.
about zero.
The Uncertainty principle states that, if ƒ(x) is absolutely continuous and the functions x·ƒ(x) and ƒ′(x) are square integrable, then
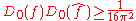 .
.
The equality is attained only in the case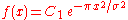 (hence
(hence  ) where σ > 0 is arbitrary and C1 is such that ƒ is L2–normalized . In other words, where ƒ is a (normalized) Gaussian function with variance σ2, centered at zero, and its Fourier transform is a Gaussian function with variance 1/σ2.
) where σ > 0 is arbitrary and C1 is such that ƒ is L2–normalized . In other words, where ƒ is a (normalized) Gaussian function with variance σ2, centered at zero, and its Fourier transform is a Gaussian function with variance 1/σ2.
In fact, this inequality implies that:
for any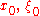 in R .
in R .
In quantum mechanics
, the momentum
and position wave functions are Fourier transform pairs, to within a factor of Planck's constant. With this constant properly taken into account, the inequality above becomes the statement of the Heisenberg uncertainty principle .
A stronger uncertainty principle is the Hirschman uncertainty principle
which is expressed as:
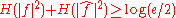
where H(p) is the differential entropy
of the probability density function
p(x):
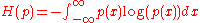
where the logarithms may be in any base which is consistent. The equality is attained for a Gaussian, as in the previous case.
harmonic
polynomial
s of degree k on Rn be denoted by Ak. The set Ak consists of the solid spherical harmonics of degree k. The solid spherical harmonics play a similar role in higher dimensions to the Hermite polynomials in dimension one. Specifically, if f(x) = e−π|x|2P(x) for some P(x) in Ak, then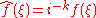 . Let the set Hk be the closure in L2(Rn) of linear combinations of functions of the form f(|x|)P(x) where P(x) is in Ak. The space L2(Rn) is then a direct sum of the spaces Hk and the Fourier transform maps each space Hk to itself and is possible to characterize the action of the Fourier transform on each space Hk . Let ƒ(x) = ƒ0(|x|)P(x) (with P(x) in Ak), then
. Let the set Hk be the closure in L2(Rn) of linear combinations of functions of the form f(|x|)P(x) where P(x) is in Ak. The space L2(Rn) is then a direct sum of the spaces Hk and the Fourier transform maps each space Hk to itself and is possible to characterize the action of the Fourier transform on each space Hk . Let ƒ(x) = ƒ0(|x|)P(x) (with P(x) in Ak), then 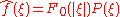 where
where
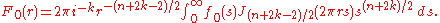
Here J(n + 2k − 2)/2 denotes the Bessel function
of the first kind with order (n + 2k − 2)/2. When k = 0 this gives a useful formula for the Fourier transform of a radial function .
One notable difference between the Fourier transform in 1 dimension versus higher dimensions concerns the partial sum operator. Consider an increasing collection of measurable sets ER indexed by R ∈ (0,∞): such as balls of radius R centered at the origin, or cubes of side 2R. For a given integrable function ƒ, consider the function ƒR defined by:
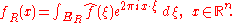
Suppose in addition that ƒ is in Lp(Rn). For n = 1 and , if one takes ER = (−R, R), then ƒR converges to ƒ in Lp as R tends to infinity, by the boundedness of the Hilbert transform
. Naively one may hope the same holds true for n > 1. In the case that ER is taken to be a cube with side length R, then convergence still holds. Another natural candidate is the Euclidean ball ER = {ξ : |ξ| < R}. In order for this partial sum operator to converge, it is necessary that the multiplier for the unit ball be bounded in Lp(Rn). For n ≥ 2 it is a celebrated theorem of Charles Fefferman
that the multiplier for the unit ball is never bounded unless p = 2 . In fact, when , this shows that not only may ƒR fail to converge to ƒ in Lp, but for some functions ƒ ∈ Lp(Rn), ƒR is not even an element of Lp.
allows us to extend the definition of the Fourier transform to general functions in L2(R) by continuity arguments. Further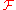 : L2(R) → L2(R) is a unitary operator
: L2(R) → L2(R) is a unitary operator
. Many of the properties remain the same for the Fourier transform. The Hausdorff–Young inequality
can be used to extend the definition of the Fourier transform to include functions in Lp(R) for 1 ≤ p ≤ 2.
Unfortunately, further extensions become more technical. The Fourier transform of functions in Lp for the range 2 < p < ∞ requires the study of distributions . In fact, it can be shown that there are functions in Lp with p>2 so that the Fourier transform is not defined as a function .

This transform continues to enjoy many of the properties of the Fourier transform of integrable functions. One notable difference is that the Riemann–Lebesgue lemma fails for measures . In the case that dμ = ƒ(x) dx, then the formula above reduces to the usual definition for the Fourier transform of ƒ. In the case that μ is the probability distribution associated to a random variable X, the Fourier-Stieltjes transform is closely related to the characteristic function
, but the typical conventions in probability theory take eix·ξ instead of e−2πix·ξ . In the case when the distribution has a probability density function
this definition reduces to the Fourier transform applied to the probability density function, again with a different choice of constants.
The Fourier transform may be used to give a characterization of continuous measures. Bochner's theorem
characterizes which functions may arise as the Fourier–Stieltjes transform of a measure .
Furthermore, the Dirac delta function
is not a function but it is a finite Borel measure. Its Fourier transform is a constant function (whose specific value depends upon the form of the Fourier transform used).
of the space to itself . Because of this it is possible to define the Fourier transform of tempered distributions. These include all the integrable functions mentioned above, as well as well-behaved functions of polynomial growth and distributions of compact support, and have the added advantage that the Fourier transform of any tempered distribution is again a tempered distribution.
The following two facts provide some motivation for the definition of the Fourier transform of a distribution. First let ƒ and g be integrable functions, and let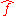 and
and 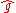 be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula ,
be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula ,
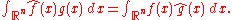
Secondly, every integrable function ƒ defines a distribution Tƒ by the relation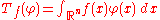 for all Schwartz functions φ.
for all Schwartz functions φ.
In fact, given a distribution T, we define the Fourier transform by the relation
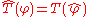 for all Schwartz functions φ.
for all Schwartz functions φ.
It follows that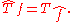
Distributions can be differentiated and the above mentioned compatibility of the Fourier transform with differentiation and convolution remains true for tempered distributions.
which is at the same time a locally compact Hausdorff topological space
so that the group operations are continuous. If G is a locally compact abelian group, it has a translation invariant measure μ, called Haar measure
. For a locally compact abelian group G it is possible to place a topology on the set of characters
 so that
so that  is also a locally compact abelian group. For a function ƒ in L1(G) it is possible to define the Fourier transform by :
is also a locally compact abelian group. For a function ƒ in L1(G) it is possible to define the Fourier transform by :
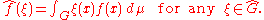
Given a locally compact
Hausdorff
topological space
X, the space A=C0(X) of continuous complex-valued functions on X which vanish at infinity is in a natural way a commutative C*-algebra, via pointwise addition, multiplication, complex conjugation, and with norm as the uniform norm. Conversely, the characters of this algebra A, denoted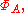 are naturally a topological space, and can be identified with evaluation at a point of x, and one has an isometric isomorphism
are naturally a topological space, and can be identified with evaluation at a point of x, and one has an isometric isomorphism 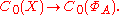 In the case where X=R is the real line, this is exactly the Fourier transform.
In the case where X=R is the real line, this is exactly the Fourier transform.
. Unlike the Fourier transform on an abelian group, which is scalar-valued, the Fourier transform on a non-abelian group is operator-valued . The Fourier transform on compact groups is a major tool in representation theory
and non-commutative harmonic analysis.
Let G be a compact Hausdorff
topological group
. Let Σ denote the collection of all isomorphism classes of finite-dimensional irreducible unitary representation
s, along with a definite choice of representation U(σ) on the Hilbert space
Hσ of finite dimension dσ for each σ ∈ Σ. If μ is a finite Borel measure on G, then the Fourier–Stieltjes transform of μ is the operator on Hσ defined by
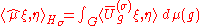
where is the complex-conjugate representation of U(σ) acting on Hσ. As in the abelian case, if μ is absolutely continuous with respect to the left-invariant probability measure
is the complex-conjugate representation of U(σ) acting on Hσ. As in the abelian case, if μ is absolutely continuous with respect to the left-invariant probability measure
λ on G, then it is represented
as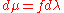
for some ƒ ∈ L1(λ)
. In this case, one identifies the Fourier transform of ƒ with the Fourier–Stieltjes transform of μ.
The mapping defines an isomorphism between the Banach space
defines an isomorphism between the Banach space
M(G) of finite Borel measures (see rca space) and a closed subspace of the Banach space
C∞(Σ) consisting of all sequences E = (Eσ) indexed by Σ of (bounded) linear operators Eσ : Hσ → Hσ for which the norm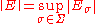
is finite. The "convolution theorem
" asserts that, furthermore, this isomorphism of Banach spaces is in fact an isomorphism of C* algebras into a subspace of C∞(Σ), in which M(G) is equipped with the product given by convolution
of measures and C∞(Σ) the product given by multiplication of operators in each index σ.
The Peter-Weyl theorem holds, and a version of the Fourier inversion formula (Plancherel's theorem) follows: if ƒ ∈ L2(G), then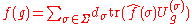
where the summation is understood as convergent in the L2 sense.
The generalization of the Fourier transform to the noncommutative situation has also in part contributed to the development of noncommutative geometry
. In this context, a categorical generalization of the Fourier transform to noncommutative groups is Tannaka-Krein duality
, which replaces the group of characters with the category of representations. However, this loses the connection with harmonic functions.
terms, a function (of time) is a representation of a signal with perfect time resolution, but no frequency information, while the Fourier transform has perfect frequency resolution, but no time information: the magnitude of the Fourier transform at a point is how much frequency content there is, but location is only given by phase (argument of the Fourier transform at a point), and standing waves are not localized in time – a sine wave continues out to infinity, without decaying. This limits the usefulness of the Fourier transform for analyzing signals that are localized in time, notably transients, or any signal of finite extent.
As alternatives to the Fourier transform, in time-frequency analysis
, one uses time-frequency transforms or time-frequency distributions to represent signals in a form that has some time information and some frequency information – by the uncertainty principle, there is a trade-off between these. These can be generalizations of the Fourier transform, such as the short-time Fourier transform
or fractional Fourier transform
, or can use different functions to represent signals, as in wavelet transforms and chirplet transforms, with the wavelet analog of the (continuous) Fourier transform being the continuous wavelet transform
. .
in the following sense: if f(x) is a differentiable function with Fourier transform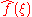 , then the Fourier transform of its derivative is given by
, then the Fourier transform of its derivative is given by 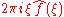 . This can be used to transform differential equations into algebraic equations. Note that this technique only applies to problems whose domain is the whole set of real numbers. By extending the Fourier transform to functions of several variables partial differential equation
. This can be used to transform differential equations into algebraic equations. Note that this technique only applies to problems whose domain is the whole set of real numbers. By extending the Fourier transform to functions of several variables partial differential equation
s with domain Rn can also be translated into algebraic equations.
(NMR) and in other kinds of spectroscopy
, e.g. infrared (FTIR
). In NMR an exponentially-shaped free induction decay (FID) signal is acquired in the time domain and Fourier-transformed to a Lorentzian line-shape in the frequency domain. The Fourier transform is also used in magnetic resonance imaging
(MRI) and mass spectrometry
.
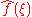 are these:
are these: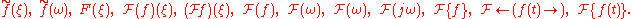
Though less commonly other notations are used. Denoting the Fourier transform by a capital letter corresponding to the letter of function being transformed (such as f(x) and F(ξ)) is especially common in the sciences and engineering. In electronics, the omega (ω) is often used instead of ξ due to its interpretation as angular frequency, sometimes it is written as F(jω), where j is the imaginary unit
, to indicate its relationship with the Laplace transform, and sometimes it is written informally as F(2πf) in order to use ordinary frequency.
The interpretation of the complex function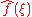 may be aided by expressing it in polar coordinate form
may be aided by expressing it in polar coordinate form
in terms of the two real functions A(ξ) and φ(ξ) where:
is the amplitude
and

is the phase
(see arg function
).
Then the inverse transform can be written:
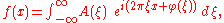
which is a recombination of all the frequency components of ƒ(x). Each component is a complex sinusoid of the form e2πixξ whose amplitude
is A(ξ) and whose initial phase angle
(at x = 0) is φ(ξ).
The Fourier transform may be thought of as a mapping on function spaces. This mapping is here denoted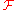 and
and 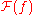 is used to denote the Fourier transform of the function f. This mapping is linear, which means that
is used to denote the Fourier transform of the function f. This mapping is linear, which means that 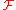 can also be seen as a linear transformation on the function space and implies that the standard notation in linear algebra of applying a linear transformation to a vector (here the function f) can be used to write
can also be seen as a linear transformation on the function space and implies that the standard notation in linear algebra of applying a linear transformation to a vector (here the function f) can be used to write 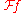 instead of
instead of 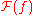 . Since the result of applying the Fourier transform is again a function, we can be interested in the value of this function evaluated at the value ξ for its variable, and this is denoted either as
. Since the result of applying the Fourier transform is again a function, we can be interested in the value of this function evaluated at the value ξ for its variable, and this is denoted either as 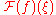 or as
or as 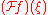 . Notice that in the former case, it is implicitly understood that
. Notice that in the former case, it is implicitly understood that 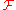 is applied first to f and then the resulting function is evaluated at ξ, not the other way around.
is applied first to f and then the resulting function is evaluated at ξ, not the other way around.
In mathematics and various applied sciences it is often necessary to distinguish between a function f and the value of f when its variable equals x, denoted f(x). This means that a notation like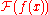 formally can be interpreted as the Fourier transform of the values of f at x. Despite this flaw, the previous notation appears frequently, often when a particular function or a function of a particular variable is to be transformed.
formally can be interpreted as the Fourier transform of the values of f at x. Despite this flaw, the previous notation appears frequently, often when a particular function or a function of a particular variable is to be transformed.
For example,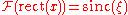 is sometimes used to express that the Fourier transform of a rectangular function is a sinc function,
is sometimes used to express that the Fourier transform of a rectangular function is a sinc function,
or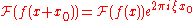 is used to express the shift property of the Fourier transform.
is used to express the shift property of the Fourier transform.
Notice, that the last example is only correct under the assumption that the transformed function is a function of x, not of x0.
: ω = 2πξ whose units are radians per second.
The substitution ξ = ω/(2π) into the formulas above produces this convention:

Under this convention, the inverse transform becomes:
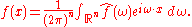
Unlike the convention followed in this article, when the Fourier transform is defined this way, it is no longer a unitary transformation
on L2(Rn). There is also less symmetry between the formulas for the Fourier transform and its inverse.
Another convention is to split the factor of (2π)n evenly between the Fourier transform and its inverse, which leads to definitions:
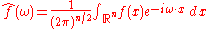
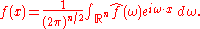
Under this convention, the Fourier transform is again a unitary transformation on L2(Rn). It also restores the symmetry between the Fourier transform and its inverse.
Variations of all three conventions can be created by conjugating the complex-exponential kernel of both the forward and the reverse transform. The signs must be opposites. Other than that, the choice is (again) a matter of convention.
As discussed above, the characteristic function
of a random variable is the same as the Fourier–Stieltjes transform of its distribution measure, but in this context it is typical to take a different convention for the constants. Typically characteristic function is defined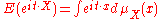 .
.
As in the case of the "non-unitary angular frequency" convention above, there is no factor of 2π
appearing in either of the integral, or in the exponential.
Unlike any of the conventions appearing above, this convention takes the opposite sign in the exponential.
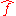 ,
, 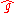 , and
, and 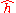 respectively. Only the three most common conventions are included.
respectively. Only the three most common conventions are included.
It may be useful to notice that entry 105 gives a relationship between the Fourier transform of a function and the original function, which can be seen as relating the Fourier transform and its inverse.
\,
|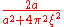
|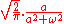
|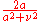
|For a>0. That is, the Fourier transform of a decaying exponential function
is a Lorentzian function.
|-
| 208
|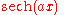
|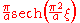
|
|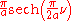
|Hyperbolic secant
is its own Fourier transform
|-
| 209
|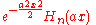
|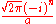
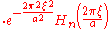
|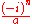
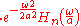
|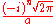
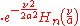
|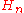 is the Hermite's polynomial. If
is the Hermite's polynomial. If  then the Gauss-Hermite functions are eigenfunctions
then the Gauss-Hermite functions are eigenfunctions
of the Fourier transform operator. For a derivation, see Hermite polynomial. The formula reduces to 206 for .
.
|}
e^{\frac{-\left(\omega_x^2/a^2 + \omega_y^2/b^2\right)}{4\pi}}
|align="center"|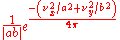
|-
|402
|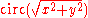
|align="center"|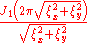
|align="center"|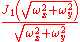
|align="center"|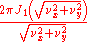
|}
Remarks
To 400: The variables ξx, ξy, ωx, ωy, νx and νy are real numbers.
The integrals are taken over the entire plane.
To 401: Both functions are Gaussians, which may not have unit volume.
To 402: The function is defined by circ(r)=1 0≤r≤1, and is 0 otherwise. This is the Airy distribution, and is expressed using J1 (the order 1 Bessel function
of the first kind).
Remarks
To 501:
The function χ[0,1] is the indicator function of the interval [0, 1]. The function Γ(x) is the gamma function. The function Jn/2 + δ is a Bessel function of the first kind, with order n/2 + δ. Taking n = 2 and δ = 0 produces 402.
To 502:
See Riesz potential
. The formula also holds for all α ≠ −n, −n − 1, ... by analytic continuation, but then the function and its Fourier transforms need to be understood as suitably regularized tempered distributions. See homogeneous distribution.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
into its constituent frequencies, known as a frequency spectrum
Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes (and phase
Phase
-In physics:*Phase , a physically distinctive form of a substance, such as the solid, liquid, and gaseous states of ordinary matter**Phase transition is the transformation of a thermodynamic system from one phase to another*Phase...
) of the individual notes that make it up. The composite waveform depends on time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, and therefore is called the time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
representation. The frequency spectrum is a function of frequency and is called the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
representation. Each value of the function is a complex number (called complex amplitude) that encodes both a magnitude and phase component. The term "Fourier transform" refers to both the transform operation and to the complex-valued function it produces.
In the case of a periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
, like the musical chord, the Fourier transform can be simplified to the calculation of a discrete set of complex amplitudes, called Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
coefficients. Also, when a time-domain function is sampled
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
to facilitate storage and/or computer-processing, it is still possible to recreate a version of the original Fourier transform according to the Poisson summation formula
Poisson summation formula
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...
, also known as discrete-time Fourier transform
Discrete-time Fourier transform
In mathematics, the discrete-time Fourier transform is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the "DTFT", of the original function . But the DTFT requires an input function...
. These topics are addressed in separate articles. For an overview of those and other related operations, refer to Fourier analysis or List of Fourier-related transforms.
Definition
There are several common conventions for defining the Fourier transform of an integrable
of an integrableLebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
function . This article will use the definition:
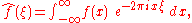 for every real number
for every real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
ξ.
When the independent variable x represents time (with SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
unit of second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s), the transform variable ξ represents frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(in hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
). Under suitable conditions, ƒ can be reconstructed from
 by the inverse transform:
by the inverse transform: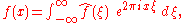 for every real number x.
for every real number x.For other common conventions and notations, including using the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
ω
Omega
Omega is the 24th and last letter of the Greek alphabet. In the Greek numeric system, it has a value of 800. The word literally means "great O" , as opposed to omicron, which means "little O"...
instead of the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
ξ, see Other conventions and Other notations below. The Fourier transform on Euclidean space is treated separately, in which the variable x often represents position and ξ momentum.
Introduction
The motivation for the Fourier transform comes from the study of Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. In the study of Fourier series, complicated functions are written as the sum of simple waves mathematically represented by sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
s and cosines. Due to the properties of sine and cosine it is possible to recover the amount of each wave in the sum by an integral. In many cases it is desirable to use Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
, which states that e2πiθ = cos 2πθ + i sin 2πθ, to write Fourier series in terms of the basic waves e2πiθ. This has the advantage of simplifying many of the formulas involved and providing a formulation for Fourier series that more closely resembles the definition followed in this article. This passage from sines and cosines to complex exponentials makes it necessary for the Fourier coefficients to be complex valued. The usual interpretation of this complex number is that it gives both the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
(or size) of the wave present in the function and the phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
(or the initial angle) of the wave. This passage also introduces the need for negative "frequencies". If θ were measured in seconds then the waves e2πiθ and e−2πiθ would both complete one cycle per second, but they represent different frequencies in the Fourier transform. Hence, frequency no longer measures the number of cycles per unit time, but is closely related.
There is a close connection between the definition of Fourier series and the Fourier transform for functions ƒ which are zero outside of an interval. For such a function we can calculate its Fourier series on any interval that includes the interval where ƒ is not identically zero. The Fourier transform is also defined for such a function. As we increase the length of the interval on which we calculate the Fourier series, then the Fourier series coefficients begin to look like the Fourier transform and the sum of the Fourier series of ƒ begins to look like the inverse Fourier transform. To explain this more precisely, suppose that T is large enough so that the interval [−T/2,T/2] contains the interval on which ƒ is not identically zero. Then the n-th series coefficient cn is given by:
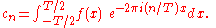
Comparing this to the definition of the Fourier transform it follows that
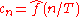 since ƒ(x) is zero outside [−T/2,T/2]. Thus the Fourier coefficients are just the values of the Fourier transform sampled on a grid of width 1/T. As T increases the Fourier coefficients more closely represent the Fourier transform of the function.
since ƒ(x) is zero outside [−T/2,T/2]. Thus the Fourier coefficients are just the values of the Fourier transform sampled on a grid of width 1/T. As T increases the Fourier coefficients more closely represent the Fourier transform of the function.Under appropriate conditions the sum of the Fourier series of ƒ will equal the function ƒ. In other words ƒ can be written:
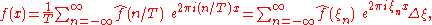
where the last sum is simply the first sum rewritten using the definitions ξn = n/T, and Δξ = (n + 1)/T − n/T = 1/T.
This second sum is a Riemann sum
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
, and so by letting T → ∞ it will converge to the integral for the inverse Fourier transform given in the definition section. Under suitable conditions this argument may be made precise .
In the study of Fourier series the numbers cn could be thought of as the "amount" of the wave in the Fourier series of ƒ. Similarly, as seen above, the Fourier transform can be thought of as a function that measures how much of each individual frequency is present in our function ƒ, and we can recombine these waves by using an integral (or "continuous sum") to reproduce the original function.
The following images provide a visual illustration of how the Fourier transform measures whether a frequency is present in a particular function. The function depicted
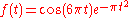 oscillates at 3 hertz (if t measures seconds) and tends quickly to 0. This function was specially chosen to have a real Fourier transform which can easily be plotted. The first image contains its graph. In order to calculate
oscillates at 3 hertz (if t measures seconds) and tends quickly to 0. This function was specially chosen to have a real Fourier transform which can easily be plotted. The first image contains its graph. In order to calculate 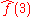
we must integrate e−2πi(3t)ƒ(t). The second image shows the plot of the real and imaginary parts of this function. The real part of the integrand is almost always positive, this is because when ƒ(t) is negative, then the real part of e−2πi(3t) is negative as well. Because they oscillate at the same rate, when ƒ(t) is positive, so is the real part of e−2πi(3t). The result is that when you integrate the real part of the integrand you get a relatively large number (in this case 0.5). On the other hand, when you try to measure a frequency that is not present, as in the case when we look at
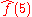 , the integrand oscillates enough so that the integral is very small. The general situation may be a bit more complicated than this, but this in spirit is how the Fourier transform measures how much of an individual frequency is present in a function ƒ(t).
, the integrand oscillates enough so that the integral is very small. The general situation may be a bit more complicated than this, but this in spirit is how the Fourier transform measures how much of an individual frequency is present in a function ƒ(t).Properties of the Fourier transform
An integrable function is a function ƒ on the real line that is Lebesgue-measurable and satisfies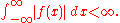
Basic properties
Given integrable functions f(x), g(x), and h(x), their Fourier transforms are denoted by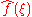 ,
, 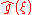 , and
, and  respectively. The Fourier transform has the following basic properties .
respectively. The Fourier transform has the following basic properties .Linearity
- For any complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s a and b, if h(x) = aƒ(x) + bg(x), then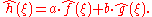
Translation
- For any real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x0, if h(x) = ƒ(x − x0), then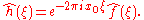
Modulation
- For any real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
ξ0, if h(x) = e2πixξ0ƒ(x), then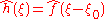 .
.
Scaling
- For a non-zero real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
a, if h(x) = ƒ(ax), then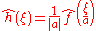 . The case a = −1 leads to the time-reversal property, which states: if h(x) = ƒ(−x), then
. The case a = −1 leads to the time-reversal property, which states: if h(x) = ƒ(−x), then 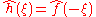 .
.
Conjugation
- If
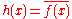 , then
, then 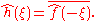
- In particular, if ƒ is real, then one has the reality condition
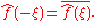
- And if ƒ is purely imaginary, then
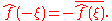
Duality
- If
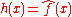 then
then 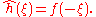
Convolution
- If
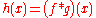 , then
, then 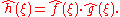
Uniform continuity and the Riemann–Lebesgue lemma

.svg.png)
The Fourier transform
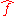 of any integrable function ƒ is uniformly continuous and
of any integrable function ƒ is uniformly continuous and  . By the Riemann–Lebesgue lemma ,
. By the Riemann–Lebesgue lemma ,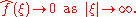
Furthermore,
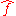 is bounded and continuous, but need not be integrable. For example, the Fourier transform of the rectangular function, which is integrable, is the sinc function, which is not Lebesgue integrable, because its improper integral
is bounded and continuous, but need not be integrable. For example, the Fourier transform of the rectangular function, which is integrable, is the sinc function, which is not Lebesgue integrable, because its improper integralImproper integral
In calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
s behave analogously to the alternating harmonic series, in converging to a sum without being absolutely convergent.
It is not generally possible to write the inverse transform as a Lebesgue integral. However, when both ƒ and
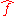 are integrable, the inverse equality
are integrable, the inverse equality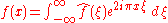
holds almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. That is, the Fourier transform is injective on L1(R)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.
(But if ƒ is continuous, then equality holds for every x.)
The Plancherel theorem and Parseval's theorem
Let f(x) and g(x) be integrable, and let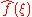 and
and 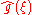 be their Fourier transforms. If f(x) and g(x) are also square-integrable, then we have Parseval's theorem
be their Fourier transforms. If f(x) and g(x) are also square-integrable, then we have Parseval's theoremParseval's theorem
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum of the square of a function is equal to the sum of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later...
:
where the bar denotes complex conjugation.
The Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
, which is equivalent to Parseval's theorem
Parseval's theorem
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum of the square of a function is equal to the sum of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later...
, states :
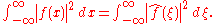
The Plancherel theorem makes it possible to define the Fourier transform for functions in L2(R), as described in Generalizations below. The Plancherel theorem has the interpretation in the sciences that the Fourier transform preserves the energy of the original quantity. It should be noted that depending on the author either of these theorems might be referred to as the Plancherel theorem or as Parseval's theorem.
See Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
for a general formulation of this concept in the context of locally compact abelian groups.
Poisson summation formula
The Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. It has a variety of useful forms that are derived from the basic one by application of the Fourier transform's scaling and time-shifting properties. One such form leads directly to a proof of the Nyquist-Shannon sampling theorem.Convolution theorem
The Fourier transform translates between convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
and multiplication of functions. If ƒ(x) and g(x) are integrable functions with Fourier transforms
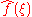 and
and 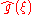 respectively, then the Fourier transform of the convolution is given by the product of the Fourier transforms
respectively, then the Fourier transform of the convolution is given by the product of the Fourier transforms 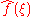 and
and 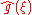 (under other conventions for the definition of the Fourier transform a constant factor may appear).
(under other conventions for the definition of the Fourier transform a constant factor may appear).This means that if:
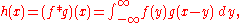
where ∗ denotes the convolution operation, then:
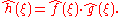
In linear time invariant (LTI) system theory
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
, it is common to interpret g(x) as the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of an LTI system with input ƒ(x) and output h(x), since substituting the unit impulse
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
for ƒ(x) yields h(x) = g(x). In this case,
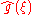 represents the frequency response
represents the frequency responseFrequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
of the system.
Conversely, if ƒ(x) can be decomposed as the product of two square integrable functions p(x) and q(x), then the Fourier transform of ƒ(x) is given by the convolution of the respective Fourier transforms
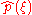 and
and 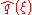 .
.Cross-correlation theorem
In an analogous manner, it can be shown that if h(x) is the cross-correlationCross-correlation
In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
of ƒ(x) and g(x):
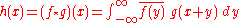
then the Fourier transform of h(x) is:
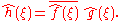
As a special case, the autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
of function ƒ(x) is:
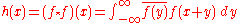
for which
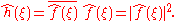
Eigenfunctions
One important choice of an orthonormal basis for L2(R)Square-integrable function
In mathematics, a quadratically integrable function, also called a square-integrable function, is a real- or complex-valued measurable function for which the integral of the square of the absolute value is finite...
is given by the Hermite functions
where
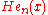 are the "probabilist's" Hermite polynomials, defined by Hen(x) = (−1)nexp(x2/2) Dn exp(−x2/2). Under this convention for the Fourier transform, we have that
are the "probabilist's" Hermite polynomials, defined by Hen(x) = (−1)nexp(x2/2) Dn exp(−x2/2). Under this convention for the Fourier transform, we have thatIn other words, the Hermite functions form a complete orthonormal system of eigenfunctions for the Fourier transform on L2(R) . However, this choice of eigenfunctions is not unique. There are only four different eigenvalues of the Fourier transform (±1 and ±i) and any linear combination of eigenfunctions with the same eigenvalue gives another eigenfunction. As a consequence of this, it is possible to decompose L2(R) as a direct sum of four spaces H0, H1, H2, and H3 where the Fourier transform acts on Hek simply by multiplication by ik. This approach to define the Fourier transform is due to N. Wiener . The choice of Hermite functions is convenient because they are exponentially localized in both frequency and time domains, and thus give rise to the fractional Fourier transform
Fractional Fourier transform
In mathematics, in the area of harmonic analysis, the fractional Fourier transform is a linear transformation generalizing the Fourier transform. It can be thought of as the Fourier transform to the n-th power where n need not be an integer — thus, it can transform a function to an...
used in time-frequency analysis .
Fourier transform on Euclidean space
The Fourier transform can be in any arbitrary number of dimensions n. As with the one-dimensional case there are many conventions, for an integrable function ƒ(x) this article takes the definition: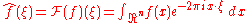
where x and ξ are n-dimensional vectors, and is the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of the vectors. The dot product is sometimes written as
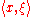 .
.All of the basic properties listed above hold for the n-dimensional Fourier transform, as do Plancherel's and Parseval's theorem. When the function is integrable, the Fourier transform is still uniformly continuous and the Riemann–Lebesgue lemma holds.
Uncertainty principle
Generally speaking, the more concentrated f(x) is, the more spread out its Fourier transform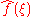 must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we "squeeze" a function in x, its Fourier transform "stretches out" in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.
must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we "squeeze" a function in x, its Fourier transform "stretches out" in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.The trade-off between the compaction of a function and its Fourier transform can be formalized in the form of an uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
by viewing a function and its Fourier transform as conjugate variables
Conjugate variables
Conjugate variables are pairs of variables mathematically defined in such a way that they become Fourier transform duals of one-another, or more generally are related through Pontryagin duality. The duality relations lead naturally to an uncertainty in physics called the Heisenberg uncertainty...
with respect to the symplectic form on the time–frequency domain: from the point of view of the linear canonical transformation
Linear canonical transformation
In Hamiltonian mechanics, the linear canonical transformation is a family of integral transforms that generalizes many classical transforms...
, the Fourier transform is rotation by 90° in the time–frequency domain, and preserves the symplectic form
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
.
Suppose ƒ(x) is an integrable and square-integrable function. Without loss of generality, assume that ƒ(x) is normalized:
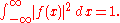
It follows from the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
that
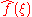 is also normalized.
is also normalized.The spread around x = 0 may be measured by the dispersion about zero defined by
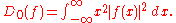
In probability terms, this is the second moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of
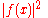 about zero.
about zero.The Uncertainty principle states that, if ƒ(x) is absolutely continuous and the functions x·ƒ(x) and ƒ′(x) are square integrable, then
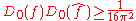 .
.The equality is attained only in the case
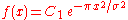 (hence
(hence  ) where σ > 0 is arbitrary and C1 is such that ƒ is L2–normalized . In other words, where ƒ is a (normalized) Gaussian function with variance σ2, centered at zero, and its Fourier transform is a Gaussian function with variance 1/σ2.
) where σ > 0 is arbitrary and C1 is such that ƒ is L2–normalized . In other words, where ƒ is a (normalized) Gaussian function with variance σ2, centered at zero, and its Fourier transform is a Gaussian function with variance 1/σ2.In fact, this inequality implies that:
for any
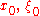 in R .
in R .In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
and position wave functions are Fourier transform pairs, to within a factor of Planck's constant. With this constant properly taken into account, the inequality above becomes the statement of the Heisenberg uncertainty principle .
A stronger uncertainty principle is the Hirschman uncertainty principle
Hirschman uncertainty
In quantum mechanics, information theory, and Fourier analysis, the Hirschman uncertainty is defined as the sum of the temporal and spectral Shannon entropies. It turns out that Heisenberg's uncertainty principle can be expressed as a lower bound on the sum of these entropies...
which is expressed as:
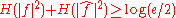
where H(p) is the differential entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
of the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
p(x):
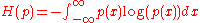
where the logarithms may be in any base which is consistent. The equality is attained for a Gaussian, as in the previous case.
Spherical harmonics
Let the set of homogeneousHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
harmonic
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s of degree k on Rn be denoted by Ak. The set Ak consists of the solid spherical harmonics of degree k. The solid spherical harmonics play a similar role in higher dimensions to the Hermite polynomials in dimension one. Specifically, if f(x) = e−π|x|2P(x) for some P(x) in Ak, then
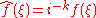 . Let the set Hk be the closure in L2(Rn) of linear combinations of functions of the form f(|x|)P(x) where P(x) is in Ak. The space L2(Rn) is then a direct sum of the spaces Hk and the Fourier transform maps each space Hk to itself and is possible to characterize the action of the Fourier transform on each space Hk . Let ƒ(x) = ƒ0(|x|)P(x) (with P(x) in Ak), then
. Let the set Hk be the closure in L2(Rn) of linear combinations of functions of the form f(|x|)P(x) where P(x) is in Ak. The space L2(Rn) is then a direct sum of the spaces Hk and the Fourier transform maps each space Hk to itself and is possible to characterize the action of the Fourier transform on each space Hk . Let ƒ(x) = ƒ0(|x|)P(x) (with P(x) in Ak), then 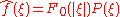 where
where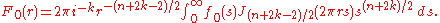
Here J(n + 2k − 2)/2 denotes the Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind with order (n + 2k − 2)/2. When k = 0 this gives a useful formula for the Fourier transform of a radial function .
Restriction problems
In higher dimensions it becomes interesting to study restriction problems for the Fourier transform. The Fourier transform of an integrable function is continuous and the restriction of this function to any set is defined. But for a square-integrable function the Fourier transform could be a general class of square integrable functions. As such, the restriction of the Fourier transform of an L2(Rn) function cannot be defined on sets of measure 0. It is still an active area of study to understand restriction problems in Lp for 1 < p < 2. Surprisingly, it is possible in some cases to define the restriction of a Fourier transform to a set S, provided S has non-zero curvature. The case when S is the unit sphere in Rn is of particular interest. In this case the Tomas-Stein restriction theorem states that the restriction of the Fourier transform to the unit sphere in Rn is a bounded operator on Lp provided 1 ≤ p ≤ .One notable difference between the Fourier transform in 1 dimension versus higher dimensions concerns the partial sum operator. Consider an increasing collection of measurable sets ER indexed by R ∈ (0,∞): such as balls of radius R centered at the origin, or cubes of side 2R. For a given integrable function ƒ, consider the function ƒR defined by:
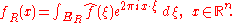
Suppose in addition that ƒ is in Lp(Rn). For n = 1 and , if one takes ER = (−R, R), then ƒR converges to ƒ in Lp as R tends to infinity, by the boundedness of the Hilbert transform
Hilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
. Naively one may hope the same holds true for n > 1. In the case that ER is taken to be a cube with side length R, then convergence still holds. Another natural candidate is the Euclidean ball ER = {ξ : |ξ| < R}. In order for this partial sum operator to converge, it is necessary that the multiplier for the unit ball be bounded in Lp(Rn). For n ≥ 2 it is a celebrated theorem of Charles Fefferman
Charles Fefferman
Charles Louis Fefferman is an American mathematician at Princeton University. His primary field of research is mathematical analysis....
that the multiplier for the unit ball is never bounded unless p = 2 . In fact, when , this shows that not only may ƒR fail to converge to ƒ in Lp, but for some functions ƒ ∈ Lp(Rn), ƒR is not even an element of Lp.
Fourier transform on other function spaces
It is possible to extend the definition of the Fourier transform to other spaces of functions. Since compactly supported smooth functions are integrable and dense in L2(R), the Plancherel theoremPlancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
allows us to extend the definition of the Fourier transform to general functions in L2(R) by continuity arguments. Further
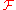 : L2(R) → L2(R) is a unitary operator
: L2(R) → L2(R) is a unitary operatorUnitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
. Many of the properties remain the same for the Fourier transform. The Hausdorff–Young inequality
Hausdorff–Young inequality
In mathematics, the Hausdorff−Young inequality bounds the Lq-norm of the Fourier coefficients of a periodic function for q ≥ 2. proved the inequality for some special values of q, and proved it in general...
can be used to extend the definition of the Fourier transform to include functions in Lp(R) for 1 ≤ p ≤ 2.
Unfortunately, further extensions become more technical. The Fourier transform of functions in Lp for the range 2 < p < ∞ requires the study of distributions . In fact, it can be shown that there are functions in Lp with p>2 so that the Fourier transform is not defined as a function .
Fourier–Stieltjes transform
The Fourier transform of a finite Borel measure μ on Rn is given by :
This transform continues to enjoy many of the properties of the Fourier transform of integrable functions. One notable difference is that the Riemann–Lebesgue lemma fails for measures . In the case that dμ = ƒ(x) dx, then the formula above reduces to the usual definition for the Fourier transform of ƒ. In the case that μ is the probability distribution associated to a random variable X, the Fourier-Stieltjes transform is closely related to the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
, but the typical conventions in probability theory take eix·ξ instead of e−2πix·ξ . In the case when the distribution has a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
this definition reduces to the Fourier transform applied to the probability density function, again with a different choice of constants.
The Fourier transform may be used to give a characterization of continuous measures. Bochner's theorem
Bochner's theorem
In mathematics, Bochner's theorem characterizes the Fourier transform of a positive finite Borel measure on the real line.- Background :...
characterizes which functions may arise as the Fourier–Stieltjes transform of a measure .
Furthermore, the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
is not a function but it is a finite Borel measure. Its Fourier transform is a constant function (whose specific value depends upon the form of the Fourier transform used).
Tempered distributions
The Fourier transform maps the space of Schwartz functions to itself, and gives a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
of the space to itself . Because of this it is possible to define the Fourier transform of tempered distributions. These include all the integrable functions mentioned above, as well as well-behaved functions of polynomial growth and distributions of compact support, and have the added advantage that the Fourier transform of any tempered distribution is again a tempered distribution.
The following two facts provide some motivation for the definition of the Fourier transform of a distribution. First let ƒ and g be integrable functions, and let
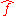 and
and 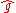 be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula ,
be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula ,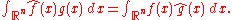
Secondly, every integrable function ƒ defines a distribution Tƒ by the relation
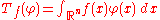 for all Schwartz functions φ.
for all Schwartz functions φ.In fact, given a distribution T, we define the Fourier transform by the relation
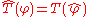 for all Schwartz functions φ.
for all Schwartz functions φ.It follows that
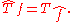
Distributions can be differentiated and the above mentioned compatibility of the Fourier transform with differentiation and convolution remains true for tempered distributions.
Locally compact abelian groups
The Fourier transform may be generalized to any locally compact abelian group. A locally compact abelian group is an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
which is at the same time a locally compact Hausdorff topological space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
so that the group operations are continuous. If G is a locally compact abelian group, it has a translation invariant measure μ, called Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
. For a locally compact abelian group G it is possible to place a topology on the set of characters
Character group
In mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory...
 so that
so that  is also a locally compact abelian group. For a function ƒ in L1(G) it is possible to define the Fourier transform by :
is also a locally compact abelian group. For a function ƒ in L1(G) it is possible to define the Fourier transform by :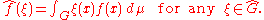
Locally compact Hausdorff space
The Fourier transform may be generalized to any locally compact Hausdorff space, which recovers the topology but loses the group structure.Given a locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, the space A=C0(X) of continuous complex-valued functions on X which vanish at infinity is in a natural way a commutative C*-algebra, via pointwise addition, multiplication, complex conjugation, and with norm as the uniform norm. Conversely, the characters of this algebra A, denoted
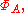 are naturally a topological space, and can be identified with evaluation at a point of x, and one has an isometric isomorphism
are naturally a topological space, and can be identified with evaluation at a point of x, and one has an isometric isomorphism 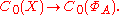 In the case where X=R is the real line, this is exactly the Fourier transform.
In the case where X=R is the real line, this is exactly the Fourier transform.Non-abelian groups
The Fourier transform can also be defined for functions on a non-abelian group, provided that the group is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. Unlike the Fourier transform on an abelian group, which is scalar-valued, the Fourier transform on a non-abelian group is operator-valued . The Fourier transform on compact groups is a major tool in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
and non-commutative harmonic analysis.
Let G be a compact Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
. Let Σ denote the collection of all isomorphism classes of finite-dimensional irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s, along with a definite choice of representation U(σ) on the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
Hσ of finite dimension dσ for each σ ∈ Σ. If μ is a finite Borel measure on G, then the Fourier–Stieltjes transform of μ is the operator on Hσ defined by
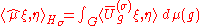
where
 is the complex-conjugate representation of U(σ) acting on Hσ. As in the abelian case, if μ is absolutely continuous with respect to the left-invariant probability measure
is the complex-conjugate representation of U(σ) acting on Hσ. As in the abelian case, if μ is absolutely continuous with respect to the left-invariant probability measureHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
λ on G, then it is represented
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
as
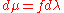
for some ƒ ∈ L1(λ)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. In this case, one identifies the Fourier transform of ƒ with the Fourier–Stieltjes transform of μ.
The mapping
 defines an isomorphism between the Banach space
defines an isomorphism between the Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
M(G) of finite Borel measures (see rca space) and a closed subspace of the Banach space
C∞(Σ) consisting of all sequences E = (Eσ) indexed by Σ of (bounded) linear operators Eσ : Hσ → Hσ for which the norm
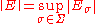
is finite. The "convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
" asserts that, furthermore, this isomorphism of Banach spaces is in fact an isomorphism of C* algebras into a subspace of C∞(Σ), in which M(G) is equipped with the product given by convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of measures and C∞(Σ) the product given by multiplication of operators in each index σ.
The Peter-Weyl theorem holds, and a version of the Fourier inversion formula (Plancherel's theorem) follows: if ƒ ∈ L2(G), then
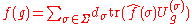
where the summation is understood as convergent in the L2 sense.
The generalization of the Fourier transform to the noncommutative situation has also in part contributed to the development of noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
. In this context, a categorical generalization of the Fourier transform to noncommutative groups is Tannaka-Krein duality
Tannaka-Krein duality
In mathematics, Tannaka–Krein duality theory concerns the interaction of a compact topological group and its category of linear representations. Its natural extension to the non-Abelian case is the Grothendieck duality theory....
, which replaces the group of characters with the category of representations. However, this loses the connection with harmonic functions.
Alternatives
In signal processingSignal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
terms, a function (of time) is a representation of a signal with perfect time resolution, but no frequency information, while the Fourier transform has perfect frequency resolution, but no time information: the magnitude of the Fourier transform at a point is how much frequency content there is, but location is only given by phase (argument of the Fourier transform at a point), and standing waves are not localized in time – a sine wave continues out to infinity, without decaying. This limits the usefulness of the Fourier transform for analyzing signals that are localized in time, notably transients, or any signal of finite extent.
As alternatives to the Fourier transform, in time-frequency analysis
Time-frequency analysis
In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains simultaneously, using various time–frequency representations...
, one uses time-frequency transforms or time-frequency distributions to represent signals in a form that has some time information and some frequency information – by the uncertainty principle, there is a trade-off between these. These can be generalizations of the Fourier transform, such as the short-time Fourier transform
Short-time Fourier transform
The short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
or fractional Fourier transform
Fractional Fourier transform
In mathematics, in the area of harmonic analysis, the fractional Fourier transform is a linear transformation generalizing the Fourier transform. It can be thought of as the Fourier transform to the n-th power where n need not be an integer — thus, it can transform a function to an...
, or can use different functions to represent signals, as in wavelet transforms and chirplet transforms, with the wavelet analog of the (continuous) Fourier transform being the continuous wavelet transform
Continuous wavelet transform
A continuous wavelet transform is used to divide a continuous-time function into wavelets. Unlike Fourier transform, the continuous wavelet transform possesses the ability to construct a time-frequency representation of a signal that offers very good time and frequency localization...
. .
Analysis of differential equations
Fourier transforms and the closely related Laplace transforms are widely used in solving differential equations. The Fourier transform is compatible with differentiationDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
in the following sense: if f(x) is a differentiable function with Fourier transform
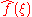 , then the Fourier transform of its derivative is given by
, then the Fourier transform of its derivative is given by 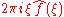 . This can be used to transform differential equations into algebraic equations. Note that this technique only applies to problems whose domain is the whole set of real numbers. By extending the Fourier transform to functions of several variables partial differential equation
. This can be used to transform differential equations into algebraic equations. Note that this technique only applies to problems whose domain is the whole set of real numbers. By extending the Fourier transform to functions of several variables partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s with domain Rn can also be translated into algebraic equations.
Fourier transform spectroscopy
The Fourier transform is also used in nuclear magnetic resonanceNuclear magnetic resonance
Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...
(NMR) and in other kinds of spectroscopy
Spectroscopy
Spectroscopy is the study of the interaction between matter and radiated energy. Historically, spectroscopy originated through the study of visible light dispersed according to its wavelength, e.g., by a prism. Later the concept was expanded greatly to comprise any interaction with radiative...
, e.g. infrared (FTIR
Fourier transform infrared spectroscopy
Fourier transform infrared spectroscopy is a technique which is used to obtain an infrared spectrum of absorption, emission, photoconductivity or Raman scattering of a solid, liquid or gas. An FTIR spectrometer simultaneously collects spectral data in a wide spectral range...
). In NMR an exponentially-shaped free induction decay (FID) signal is acquired in the time domain and Fourier-transformed to a Lorentzian line-shape in the frequency domain. The Fourier transform is also used in magnetic resonance imaging
Magnetic resonance imaging
Magnetic resonance imaging , nuclear magnetic resonance imaging , or magnetic resonance tomography is a medical imaging technique used in radiology to visualize detailed internal structures...
(MRI) and mass spectrometry
Mass spectrometry
Mass spectrometry is an analytical technique that measures the mass-to-charge ratio of charged particles.It is used for determining masses of particles, for determining the elemental composition of a sample or molecule, and for elucidating the chemical structures of molecules, such as peptides and...
.
Domain and range of the Fourier transform
It is often desirable to have the most general domain for the Fourier transform possible. The definition of Fourier transform as an integral naturally restricts the domain to the space of integrable functions. Unfortunately, there is no simple characterization of which functions are Fourier transforms of integrable functions . It is possible to extend the domain of the Fourier transform in various ways, as discussed in the generalizations above. The following list details some of the more common domains and ranges on which the Fourier transform is defined.- The space of Schwartz functions is closed under the Fourier transform. Schwartz functions are rapidly decaying functions and do not include all functions which are relevant for the Fourier transform. More details may be found in .
- The space Lp maps into the space Lq, where 1/p + 1/q = 1 and 1 ≤ p ≤ 2 (Hausdorff–Young inequalityHausdorff–Young inequalityIn mathematics, the Hausdorff−Young inequality bounds the Lq-norm of the Fourier coefficients of a periodic function for q ≥ 2. proved the inequality for some special values of q, and proved it in general...
).
- In particular, the space L2 is closed under the Fourier transform, but here the Fourier transform is no longer defined by integration.
- The space L1 of Lebesgue integrable functions maps into C0, the space of continuous functions that tend to zero at infinity – not just into the space
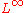 of bounded functions (the Riemann–Lebesgue lemma).
of bounded functions (the Riemann–Lebesgue lemma).
- The set of tempered distributions is closed under the Fourier transform. Tempered distributions are also a form of generalization of functions. It is in this generality that one can define the Fourier transform of objects like the Dirac combDirac combIn mathematics, a Dirac comb is a periodic Schwartz distribution constructed from Dirac delta functions...
.
Other notations
Other common notations for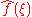 are these:
are these: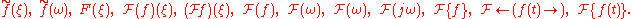
Though less commonly other notations are used. Denoting the Fourier transform by a capital letter corresponding to the letter of function being transformed (such as f(x) and F(ξ)) is especially common in the sciences and engineering. In electronics, the omega (ω) is often used instead of ξ due to its interpretation as angular frequency, sometimes it is written as F(jω), where j is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
, to indicate its relationship with the Laplace transform, and sometimes it is written informally as F(2πf) in order to use ordinary frequency.
The interpretation of the complex function
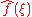 may be aided by expressing it in polar coordinate form
may be aided by expressing it in polar coordinate form
in terms of the two real functions A(ξ) and φ(ξ) where:

is the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
and

is the phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
(see arg function
Arg (mathematics)
In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
).
Then the inverse transform can be written:
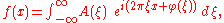
which is a recombination of all the frequency components of ƒ(x). Each component is a complex sinusoid of the form e2πixξ whose amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
is A(ξ) and whose initial phase angle
Phase angle
In the context of vectors and phasors, the term phase angle refers to the angular component of the polar coordinate representation. The notation A\ang \!\ \theta, for a vector with magnitude A and phase angle θ, is called angle notation.In the context of periodic phenomena, such as a wave,...
(at x = 0) is φ(ξ).
The Fourier transform may be thought of as a mapping on function spaces. This mapping is here denoted
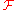 and
and 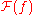 is used to denote the Fourier transform of the function f. This mapping is linear, which means that
is used to denote the Fourier transform of the function f. This mapping is linear, which means that 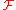 can also be seen as a linear transformation on the function space and implies that the standard notation in linear algebra of applying a linear transformation to a vector (here the function f) can be used to write
can also be seen as a linear transformation on the function space and implies that the standard notation in linear algebra of applying a linear transformation to a vector (here the function f) can be used to write 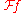 instead of
instead of 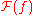 . Since the result of applying the Fourier transform is again a function, we can be interested in the value of this function evaluated at the value ξ for its variable, and this is denoted either as
. Since the result of applying the Fourier transform is again a function, we can be interested in the value of this function evaluated at the value ξ for its variable, and this is denoted either as 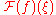 or as
or as 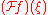 . Notice that in the former case, it is implicitly understood that
. Notice that in the former case, it is implicitly understood that  is applied first to f and then the resulting function is evaluated at ξ, not the other way around.
is applied first to f and then the resulting function is evaluated at ξ, not the other way around.In mathematics and various applied sciences it is often necessary to distinguish between a function f and the value of f when its variable equals x, denoted f(x). This means that a notation like
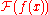 formally can be interpreted as the Fourier transform of the values of f at x. Despite this flaw, the previous notation appears frequently, often when a particular function or a function of a particular variable is to be transformed.
formally can be interpreted as the Fourier transform of the values of f at x. Despite this flaw, the previous notation appears frequently, often when a particular function or a function of a particular variable is to be transformed.For example,
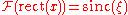 is sometimes used to express that the Fourier transform of a rectangular function is a sinc function,
is sometimes used to express that the Fourier transform of a rectangular function is a sinc function,or
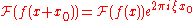 is used to express the shift property of the Fourier transform.
is used to express the shift property of the Fourier transform.Notice, that the last example is only correct under the assumption that the transformed function is a function of x, not of x0.
Other conventions
The Fourier transform can also be written in terms of angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
: ω = 2πξ whose units are radians per second.
The substitution ξ = ω/(2π) into the formulas above produces this convention:

Under this convention, the inverse transform becomes:
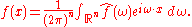
Unlike the convention followed in this article, when the Fourier transform is defined this way, it is no longer a unitary transformation
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
on L2(Rn). There is also less symmetry between the formulas for the Fourier transform and its inverse.
Another convention is to split the factor of (2π)n evenly between the Fourier transform and its inverse, which leads to definitions:
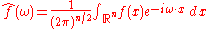
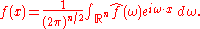
Under this convention, the Fourier transform is again a unitary transformation on L2(Rn). It also restores the symmetry between the Fourier transform and its inverse.
Variations of all three conventions can be created by conjugating the complex-exponential kernel of both the forward and the reverse transform. The signs must be opposites. Other than that, the choice is (again) a matter of convention.
| ordinary frequency ξ (hertz) | unitary | 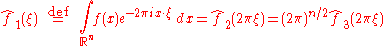 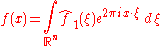 |
|---|---|---|
| angular frequency ω (rad/s) | non-unitary | 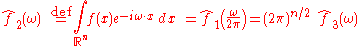 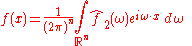 |
| unitary | 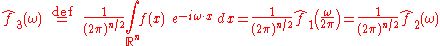 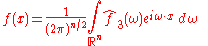 |
As discussed above, the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of a random variable is the same as the Fourier–Stieltjes transform of its distribution measure, but in this context it is typical to take a different convention for the constants. Typically characteristic function is defined
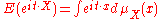 .
.As in the case of the "non-unitary angular frequency" convention above, there is no factor of 2π
appearing in either of the integral, or in the exponential.
Unlike any of the conventions appearing above, this convention takes the opposite sign in the exponential.
Tables of important Fourier transforms
The following tables record some closed form Fourier transforms. For functions ƒ(x) , g(x) and h(x) denote their Fourier transforms by ,
, 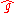 , and
, and 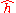 respectively. Only the three most common conventions are included.
respectively. Only the three most common conventions are included.It may be useful to notice that entry 105 gives a relationship between the Fourier transform of a function and the original function, which can be seen as relating the Fourier transform and its inverse.
Functional relationships
The Fourier transforms in this table may be found in or the appendix of .| Function | Fourier transform unitary, ordinary frequency | Fourier transform unitary, angular frequency | Fourier transform non-unitary, angular frequency | Remarks | |
|---|---|---|---|---|---|
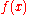 |
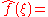  |
 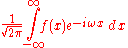 |
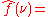 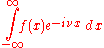 |
Definition | |
| 101 |  |
 |
 |
 |
Linearity |
| 102 | 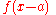 |
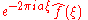 |
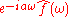 |
 |
Shift in time domain |
| 103 | 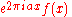 |
 |
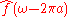 |
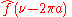 |
Shift in frequency domain, dual of 102 |
| 104 | 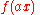 |
is large, then 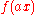 is concentrated around 0 and is concentrated around 0 and 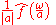 spreads out and flattens. spreads out and flattens. |
|||
| 105 | 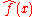 |
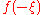 |
 |
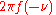 |
Duality. Here 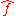 needs to be calculated using the same method as Fourier transform column. Results from swapping "dummy" variables of needs to be calculated using the same method as Fourier transform column. Results from swapping "dummy" variables of  and and 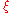 or or  or or  . . |
| 106 | 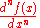 |
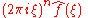 |
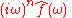 |
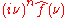 |
|
| 107 | 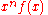 |
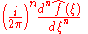 |
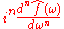 |
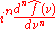 |
This is the dual of 106 |
| 108 | 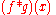 |
 |
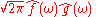 |
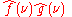 |
The notation  denotes the convolution denotes the convolutionConvolution In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation... of 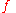 and and 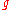 — this rule is the convolution theorem — this rule is the convolution theoremConvolution theorem In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain... |
| 109 | 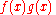 |
 |
 |
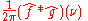 |
This is the dual of 108 |
| 110 | For 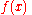 a purely real a purely real |
 |
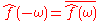 |
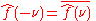 |
Hermitian symmetry.  indicates the complex conjugate indicates the complex conjugateComplex conjugate In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs... . |
| 111 | For 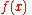 a purely real even function a purely real even function |
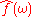 , , 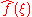 and and 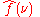 are purely real even functions. are purely real even functions. |
|||
| 112 | For 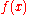 a purely real odd function a purely real odd function |
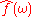 , ,  and and 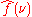 are purely imaginary are purely imaginaryImaginary number An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative... odd functions. |
|||
Square-integrable functions
The Fourier transforms in this table may be found in , , or the appendix of .| Function | Fourier transform unitary, ordinary frequency | Fourier transform unitary, angular frequency | Fourier transform non-unitary, angular frequency | Remarks | |
|---|---|---|---|---|---|
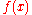 |
 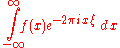 |
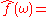 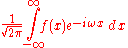 |
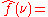 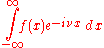 |
||
| 201 |  |
 |
The rectangular pulse and the normalized sinc function, here defined as sinc(x) = sin(πx)/(πx) | ||
| 202 | 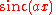 |
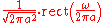 |
Dual of rule 201. The rectangular function is an ideal low-pass filter Low-pass filter A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter... , and the sinc function is the non-causal impulse response of such a filter. |
||
| 203 | 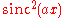 |
 |
The function tri(x) is the triangular function | ||
| 204 |  |
 |
Dual of rule 203. | ||
| 205 | 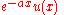 |
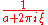 |
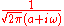 |
 |
The function u(x) is the Heaviside unit step function Heaviside step function The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument.... and a>0. |
| 206 | 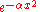 |
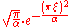 |
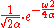 |
 |
This shows that, for the unitary Fourier transforms, the Gaussian function exp(−αx2) is its own Fourier transform for some choice of α. For this to be integrable we must have Re(α)>0. |
| 207 |
|
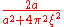
|
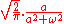
|
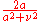
|For a>0. That is, the Fourier transform of a decaying exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
is a Lorentzian function.
|-
| 208
|
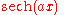
|
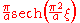
|

|
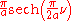
|Hyperbolic secant
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
is its own Fourier transform
|-
| 209
|
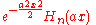
|
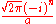
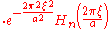
|
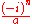
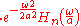
|
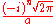
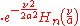
|
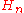 is the Hermite's polynomial. If
is the Hermite's polynomial. If  then the Gauss-Hermite functions are eigenfunctions
then the Gauss-Hermite functions are eigenfunctionsEigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
of the Fourier transform operator. For a derivation, see Hermite polynomial. The formula reduces to 206 for
 .
.|}
Distributions
The Fourier transforms in this table may be found in or the appendix of .| Function | Fourier transform unitary, ordinary frequency | Fourier transform unitary, angular frequency | Fourier transform non-unitary, angular frequency | Remarks | ||
|---|---|---|---|---|---|---|
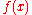 |
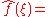 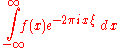 |
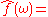 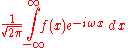 |
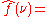 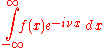 |
|||
| 301 | 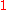 |
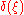 |
 |
 |
The distribution δ(ξ) denotes the Dirac delta function Dirac delta function The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical... . |
|
| 302 | 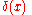 |
 |
 |
 |
Dual of rule 301. | |
| 303 | 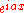 |
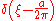 |
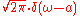 |
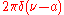 |
This follows from 103 and 301. | |
| 304 | 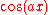 |
 |
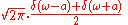 |
 |
This follows from rules 101 and 303 using Euler's formula: 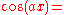  |
|
| 305 | 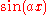 |
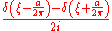 |
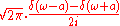 |
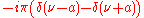 |
This follows from 101 and 303 using 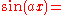 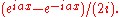 |
|
| 306 | 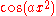 |
 |
 |
 |
||
| 307 | 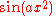 |
 |
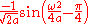 |
 |
||
| 308 | 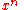 |
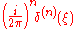 |
 |
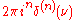 |
Here, n is a natural number Natural number In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively... and 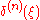 is the n-th distribution derivative of the Dirac delta function. This rule follows from rules 107 and 301. Combining this rule with 101, we can transform all polynomial is the n-th distribution derivative of the Dirac delta function. This rule follows from rules 107 and 301. Combining this rule with 101, we can transform all polynomialPolynomial In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents... s. |
|
| 309 | 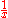 |
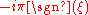 |
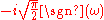 |
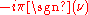 |
Here sgn(ξ) is the sign function Sign function In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function .... . Note that 1/x is not a distribution. It is necessary to use the Cauchy principal value Cauchy principal value In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:... when testing against Schwartz functions. This rule is useful in studying the Hilbert transform Hilbert transform In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the... . |
|
| 310 |  |
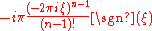 |
 |
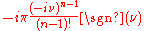 |
xn is the homogeneous distribution defined by the distributional derivative 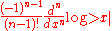 |
|
| 311 | α > −1. For α > 0 some singular terms arise at the origin that can be found by differentiating 318. If Re α > −1, then 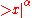 is a locally integrable function, and so a tempered distribution. The function is a locally integrable function, and so a tempered distribution. The function 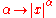 is a holomorphic function from the right half-plane to the space of tempered distributions. It admits a unique meromorphic extension to a tempered distribution, also denoted is a holomorphic function from the right half-plane to the space of tempered distributions. It admits a unique meromorphic extension to a tempered distribution, also denoted 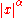 for α ≠ −2, −4, ... (See homogeneous distribution.) for α ≠ −2, −4, ... (See homogeneous distribution.) |
|||||
| 312 | 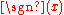 |
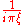 |
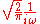 |
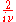 |
The dual of rule 309. This time the Fourier transforms need to be considered as Cauchy principal value Cauchy principal value In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:... . |
|
| 313 |  |
 |
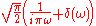 |
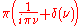 |
The function u(x) is the Heaviside unit step function Heaviside step function The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument.... ; this follows from rules 101, 301, and 312. |
|
| 314 | 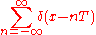 |
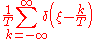 |
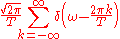 |
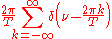 |
This function is known as the Dirac comb Dirac comb In mathematics, a Dirac comb is a periodic Schwartz distribution constructed from Dirac delta functions... function. This result can be derived from 302 and 102, together with the fact that 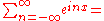 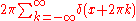 as distributions. as distributions. |
|
| 315 | 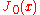 |
 |
 |
 |
The function J0(x) is the zeroth order Bessel function Bessel function In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:... of first kind. |
|
| 316 | 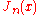 |
 |
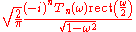 |
 |
This is a generalization of 315. The function Jn(x) is the n-th order Bessel function Bessel function In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:... of first kind. The function Tn(x) is the Chebyshev polynomial of the first kind Chebyshev polynomials In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and... . |
|
| 317 |  is the Euler–Mascheroni constant is the Euler–Mascheroni constantEuler–Mascheroni constant The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter .... . |
|||||
| 318 |  |
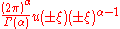 |
 |
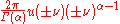 |
This formula is valid for 1 > α > 0. Use differentiation to drive formula for higher exponents.  is the Heaviside function. is the Heaviside function. |
Two-dimensional functions
| Function | Fourier transform unitary, ordinary frequency | Fourier transform unitary, angular frequency | Fourier transform non-unitary, angular frequency |
|
|---|---|---|---|---|
| 400 |  |
  |
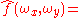 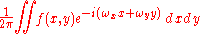 |
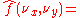 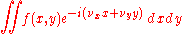 |
| 401 | 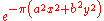 |
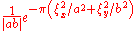 |
|align="center"|
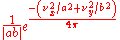
|-
|402
|
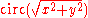
|align="center"|
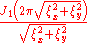
|align="center"|
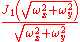
|align="center"|
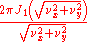
|}
Remarks
To 400: The variables ξx, ξy, ωx, ωy, νx and νy are real numbers.
The integrals are taken over the entire plane.
To 401: Both functions are Gaussians, which may not have unit volume.
To 402: The function is defined by circ(r)=1 0≤r≤1, and is 0 otherwise. This is the Airy distribution, and is expressed using J1 (the order 1 Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind).
Formulas for general n-dimensional functions
| Function | Fourier transform unitary, ordinary frequency | Fourier transform unitary, angular frequency | Fourier transform non-unitary, angular frequency |
|
|---|---|---|---|---|
| 500 |  |
 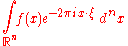 |
  |
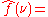  |
| 501 | 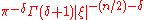 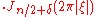 |
  |
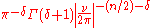 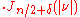 |
|
| 502 | 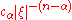 |
Remarks
To 501:
The function χ[0,1] is the indicator function of the interval [0, 1]. The function Γ(x) is the gamma function. The function Jn/2 + δ is a Bessel function of the first kind, with order n/2 + δ. Taking n = 2 and δ = 0 produces 402.
To 502:
See Riesz potential
Riesz potential
In mathematics, the Riesz potential is a potential named after its discoverer, the Hungarian mathematician Marcel Riesz. In a sense, the Riesz potential defines an inverse for a power of the Laplace operator on Euclidean space...
. The formula also holds for all α ≠ −n, −n − 1, ... by analytic continuation, but then the function and its Fourier transforms need to be understood as suitably regularized tempered distributions. See homogeneous distribution.
External links
- The Discrete Fourier Transformation (DFT): Definition and numerical examples - A Matlab tutorial
- Fourier Series Applet (Tip: drag magnitude or phase dots up or down to change the wave form).
- Stephan Bernsee's FFTlab (Java Applet)
- Stanford Video Course on the Fourier Transform
- The DFT “à Pied”: Mastering The Fourier Transform in One Day at The DSP Dimension
- An Interactive Flash Tutorial for the Fourier Transform