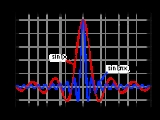
Sinc function
The sinc function, denoted by , has two definitions, sometimes distinguished as the
normalized sinc function and
unnormalized sinc function:
# In digital signal processing and
communication theory, the normalized sinc function is commonly defined by
#
# In
mathematics, the historical unnormalized sinc function , is defined by
#
In both cases, the value of the function at the removable singularity at zero is sometimes specified explicitly as 1. The sinc function is analytic everywhere.
Encyclopedia
The
sinc function, denoted by , has two definitions, sometimes distinguished as the
normalized sinc function and
unnormalized sinc function:
- In digital signal processing and communication theory, the normalized sinc function is commonly defined by
- In mathematics, the historical unnormalized sinc function , is defined by
In both cases, the value of the function at the removable singularity at zero is sometimes specified explicitly as 1. The sinc function is analytic everywhere.
Properties
The
normalized sinc function has properties that make it ideal in relationship to
interpolation and
bandlimited functions:
- and for and ; that is, it is an interpolating function.
- the functions form an orthonormal basis for bandlimited functions in the function space , with highest angular frequency .
Other properties of the two sinc functions include:
- The local maxima and minima of the unnormalized sinc, correspond to its intersections with the cosine function. I.e. where the derivative of is zero , then .
- The unnormalized sinc is the zeroth order spherical Bessel function of the first kind, . The normalized sinc is .
- The zero-crossings of the unnormalized sinc are at nonzero multiples of ; zero-crossing of the normalized sinc occur at nonzero integer values.
- The continuous Fourier transform of the normalized sinc is .
- ,
- where the rectangular function
...
is 1 for argument between –1/2 and 1/2, and zero otherwise.
- is an improper integral. It is not a Lebesgue integral because:
- where is the gamma function.
Relationship to the Dirac delta distribution
The normalized sinc function can be used as a
nascent delta function, even though it is not a distribution.
The
normalized sinc function is related to the
delta distribution δ by
This is not an ordinary limit, since the left side does not converge. Rather, it means that
for any smooth function with compact support.
In the above expression, as
a approaches zero, the number of oscillations per unit length of the sinc function approaches infinity. Nevertheless, the expression always oscillates inside an envelope of ±1/, regardless of the value of
a. This contradicts the informal picture of δ as being zero for all
x except at the point
x=0 and illustrates the problem of thinking of the delta function as a function rather than as a distribution. A similar situation is found in the
Gibbs phenomenon.
See also
External links
.svg.png)
