
Bandlimited
Encyclopedia
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
signal's Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
or power spectral density to zero above a certain finite frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
. In other words, if the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
or power spectral density has finite support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
then the signal is said to be bandlimited.
Sampling bandlimited signals
A bandlimited signal can be fully reconstructed from its samples, provided that the sampling rate exceeds twice the maximum frequency in the bandlimited signal. This minimum sampling frequency is called the Nyquist rateNyquist rate
In signal processing, the Nyquist rate, named after Harry Nyquist, is two times the bandwidth of a bandlimited signal or a bandlimited channel...
. This result, usually attributed to Nyquist
Harry Nyquist
Harry Nyquist was an important contributor to information theory.-Personal life:...
and Shannon, is known as the Nyquist–Shannon sampling theorem
Nyquist–Shannon sampling theorem
The Nyquist–Shannon sampling theorem, after Harry Nyquist and Claude Shannon, is a fundamental result in the field of information theory, in particular telecommunications and signal processing. Sampling is the process of converting a signal into a numeric sequence...
, or simply the sampling theorem.
An example of a simple deterministic bandlimited signal is a sinusoid of the form
 . If this signal is sampled at a rate
. If this signal is sampled at a rate  so that we have the samples
so that we have the samples  , for all integers
, for all integers  , we can recover
, we can recover  completely from these samples. Similarly, sums of sinusoids with different frequencies and phases are also bandlimited to the highest of their frequencies.
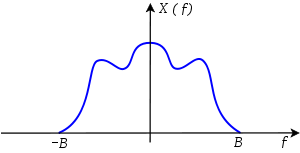
completely from these samples. Similarly, sums of sinusoids with different frequencies and phases are also bandlimited to the highest of their frequencies.The signal whose Fourier transform is shown in the figure is also bandlimited. Suppose
 is a signal whose Fourier transform is
is a signal whose Fourier transform is  , the magnitude of which is shown in the figure. The highest frequency component in
, the magnitude of which is shown in the figure. The highest frequency component in  is
is  . As a result, the Nyquist rate is
. As a result, the Nyquist rate is
or twice the highest frequency component in the signal, as shown in the figure. According to the sampling theorem, it is possible to reconstruct
 completely and exactly using the samples
completely and exactly using the samples for all integers
for all integers  and
and 
as long as

The reconstruction of a signal from its samples can be accomplished using the Whittaker–Shannon interpolation formula
Whittaker–Shannon interpolation formula
The Whittaker–Shannon interpolation formula or sinc interpolation is a method to reconstruct a continuous-time bandlimited signal from a set of equally spaced samples.-Definition:...
.
Bandlimited versus timelimited
A bandlimited signal cannot be also timelimited. More precisely, a function and its Fourier transform cannot both have finite supportSupport (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
. This fact can be proved by using complex analysis and properties of Fourier transform.
Proof: Assume that a signal f(t) which has finite support in both domains exists. Let's sample it faster than the Nyquist frequency, and compute respective Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
 and discrete-time fourier transform
and discrete-time fourier transformDiscrete-time Fourier transform
In mathematics, the discrete-time Fourier transform is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the "DTFT", of the original function . But the DTFT requires an input function...
 . According to properties of DTFT,
. According to properties of DTFT,  , where
, where  is the frequency used for discretization. If f is bandlimited,
is the frequency used for discretization. If f is bandlimited,  is zero outside of a certain interval, so with large enough
is zero outside of a certain interval, so with large enough  ,
,  will be zero in some intervals too, since individual supports
will be zero in some intervals too, since individual supportsSupport (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of
 in sum of
in sum of  won't overlap. According to DTFT definition,
won't overlap. According to DTFT definition,  is a sum of trigonometric functions, and since f(t) is time-limited, this sum will be finite, so
is a sum of trigonometric functions, and since f(t) is time-limited, this sum will be finite, so  will be actually a trigonometric polynomial
will be actually a trigonometric polynomialTrigonometric polynomial
In the mathematical subfields of numerical analysis and mathematical analysis, a trigonometric polynomial is a finite linear combination of functions sin and cos with n a natural number. The coefficients may be taken as real numbers, for real-valued functions...
. All trigonometric polynomials are holomorphic on a whole complex plane
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
, and there is a simple theorem in complex analysis that says that all zeros of non-constant holomorphic function are isolated
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
. But this contradicts to our earlier finding that
 have intervals full of zeros, because points in such interval are not isolated. Thus the only time- and bandwidth-limited signal is a constant zero.
have intervals full of zeros, because points in such interval are not isolated. Thus the only time- and bandwidth-limited signal is a constant zero.One important consequence of this result is that it is impossible to generate a truly bandlimited signal in any real-world situation, because a bandlimited signal would require infinite time to transmit. All real-world signals are, by necessity, timelimited, which means that they cannot be bandlimited. Nevertheless, the concept of a bandlimited signal is a useful idealization for theoretical and analytical purposes. Furthermore, it is possible to approximate a bandlimited signal to any arbitrary level of accuracy desired.
A similar relationship between duration in time and bandwidth in frequency also forms the mathematical basis for the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. In that setting, the "width" of the time domain and frequency domain functions are evaluated with a variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
-like measure. Quantitatively, the uncertainty principle imposes the following condition on any real waveform:

where
 is a (suitably chosen) measure of bandwidth (in hertz), and
is a (suitably chosen) measure of bandwidth (in hertz), and is a (suitably chosen) measure of time duration (in seconds).
is a (suitably chosen) measure of time duration (in seconds).In time–frequency analysis, these limits are known as the Gabor limit, and are interpreted as a limit on the simultaneous time–frequency resolution one may achieve.
See also
- Bandwidth
- Nyquist–Shannon sampling theoremNyquist–Shannon sampling theoremThe Nyquist–Shannon sampling theorem, after Harry Nyquist and Claude Shannon, is a fundamental result in the field of information theory, in particular telecommunications and signal processing. Sampling is the process of converting a signal into a numeric sequence...
- Nyquist rateNyquist rateIn signal processing, the Nyquist rate, named after Harry Nyquist, is two times the bandwidth of a bandlimited signal or a bandlimited channel...
- Nyquist frequencyNyquist frequencyThe Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system...

