Removable singularity
Encyclopedia
In complex analysis
, a removable singularity (sometimes called a cosmetic singularity) of a holomorphic function
is a point at which the function is undefined, but it is possible to define the function at that point in such a way that the function is regular in a neighbourhood of that point.
For instance, the function
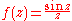
has a singularity at z = 0. This singularity can be removed by defining f(0) := 1, which is the limit
of f as z tends to 0. The resulting function is holomorphic. In this case the problem was caused by f being given an indeterminate form
. Taking a power series expansion for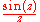
shows that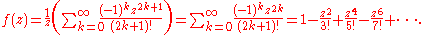
Formally, if U is an open subset of the complex plane
C, a is a point of U, and f: U − {a} → C is a holomorphic function
, then a is called a removable singularity for f if there exists a holomorphic function g: U → C which coincides with f on U − {a}. We say f is holomorphically extendable over U if such a g exists.
theorem on removable singularities states when a singularity is removable:
Theorem. Let D be an open subset of the complex plane, a a point of D and f a holomorphic function defined on the set D \ {a}. The following are equivalent:
The implications 1 ⇒ 2 ⇒ 3 ⇒ 4 are trivial. To prove 4 ⇒ 1, we first recall that the holomorphy of a function at a is equivalent to it being analytic at a (proof), i.e. having a power series representation. Define
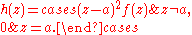
Clearly, h is holomorphic on D \ {a}, and there exists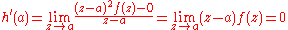
by 4, hence h is holomorphic on D and has a Taylor series about a:
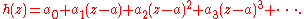
We have a0 = h(a) = 0 and a1 = h(a) = 0; therefore
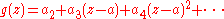
is a holomorphic extension of f over a, which proves the claim.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a removable singularity (sometimes called a cosmetic singularity) of a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
is a point at which the function is undefined, but it is possible to define the function at that point in such a way that the function is regular in a neighbourhood of that point.
For instance, the function
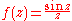
has a singularity at z = 0. This singularity can be removed by defining f(0) := 1, which is the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
of f as z tends to 0. The resulting function is holomorphic. In this case the problem was caused by f being given an indeterminate form
Indeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
. Taking a power series expansion for
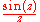shows that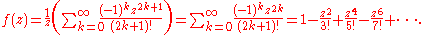Formally, if U is an open subset of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C, a is a point of U, and f: U − {a} → C is a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
, then a is called a removable singularity for f if there exists a holomorphic function g: U → C which coincides with f on U − {a}. We say f is holomorphically extendable over U if such a g exists.
Riemann's theorem
Riemann'sBernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
theorem on removable singularities states when a singularity is removable:
Theorem. Let D be an open subset of the complex plane, a a point of D and f a holomorphic function defined on the set D \ {a}. The following are equivalent:
- f is holomorphically extendable over a.
- f is continuously extendable over a.
- There exists a neighborhood of a on which f is boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
. -
.
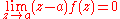The implications 1 ⇒ 2 ⇒ 3 ⇒ 4 are trivial. To prove 4 ⇒ 1, we first recall that the holomorphy of a function at a is equivalent to it being analytic at a (proof), i.e. having a power series representation. Define
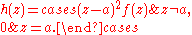
Clearly, h is holomorphic on D \ {a}, and there exists
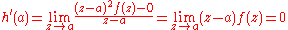
by 4, hence h is holomorphic on D and has a Taylor series about a:
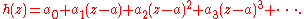
We have a0 = h(a) = 0 and a1 = h(a) = 0; therefore
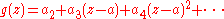
is a holomorphic extension of f over a, which proves the claim.
Other kinds of singularities
Unlike functions of a real variable, holomorphic functions are sufficiently rigid that their isolated singularities can be completely classified. A holomorphic function's singularity is either not really a singularity at all, i.e. a removable singularity, or one of the following two types:- In light of Riemann's theorem, given a non-removable singularity, one might ask whether there exists a natural number m such that limz → a(z − a)m+1f(z) = 0. If so, a is called a pole of f and the smallest such m is the order of a. So removable singularities are precisely the poles of order 0. A holomorphic function blows up uniformly near its poles.
- If an isolated singularity a of f is neither removable nor a pole, it is called an essential singularityEssential singularityIn complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
. It can be shown that such an f maps every punctured open neighborhood U − {a} to the entire complex plane, with the possible exception of at most one point.