In complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.

The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the other two categories of singularity that may be dealt with in some manner – removable singularities and poles.

Formal description

Consider an open subset

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 U of the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

 C. Let a be an element of U, and f : U \ {a} → C a meromorphic function

Meromorphic function

In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...

. The point a is called an essential singularity of the function f if the singularity is neither a pole nor a removable singularity.

For example, the function f(z) = e^1/z has an essential singularity at z = 0.

Alternate descriptions

Let a be a complex number, assume that f(z) is not defined at a but is analytic

Analytic function

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...

 in some region U of the complex plane, and that every open

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 neighbourhood

Neighbourhood (mathematics)

In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...

 of a has non-empty intersection with U.

If both 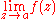  and 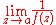    exist, then a is a removable singularity of both f and 1/f.

If   exists but 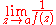    does not exist, then a is a zero

Zero (complex analysis)

In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...

 of f and a pole  of 1/f.

Similarly, if 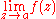  does not exist but     does exist, then a is a pole of f and a zero of 1/f.

If neithe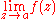r   nor 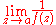    exists, then a is an essential singularity of both f and 1/f.

Another way to characterize an essential singularity is that the Laurent series

Laurent series

In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...

 of f at the point a has infinitely many negative degree terms (i.e., the principal part

Principal part

In mathematics, the principal part has several independent meanings, but usually refers to the negative-power portion of the Laurent series of a function.-Laurent series definition:...

 of the Laurent series is an infinite sum).

The behavior of meromorphic functions near essential singularities is described by the Casorati–Weierstrass theorem and by the considerably stronger Picard's great theorem. The latter says that in every neighborhood of an essential singularity a, the function f takes on every complex value, except possibly one, infinitely many times.

External links

• An Essential Singularity by Stephen Wolfram
  Stephen Wolfram
  Stephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
  
  , Wolfram Demonstrations Project
  Wolfram Demonstrations Project
  The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
  
  .
• Essential Singularity on Planet Math