Principal part
Encyclopedia
In mathematics
, the principal part has several independent meanings, but usually refers to the negative-power portion of the Laurent series
of a function.
of a function
is the portion of the Laurent series
consisting of terms with negative degree. That is,
is the principal part of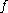
at 
.
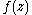has an essential singularity
at
, if and only if the principal part is an infinite sum.
and the actual increment: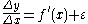
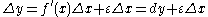
The differential
dy is sometimes called the principal (linear) part of the function increment Δy.
having a singular support at a single point.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the principal part has several independent meanings, but usually refers to the negative-power portion of the Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
of a function.
Laurent series definition
The principal part at of a function
is the portion of the Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
consisting of terms with negative degree. That is,
is the principal part of
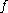at . 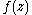has an essential singularityEssential singularity
In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
at
, if and only if the principal part is an infinite sum.Calculus
Consider the difference between the function differentialDifferential (mathematics)
In mathematics, the term differential has several meanings.-Basic notions:* In calculus, the differential represents a change in the linearization of a function....
and the actual increment:
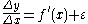
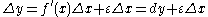
The differential
Differential (mathematics)
In mathematics, the term differential has several meanings.-Basic notions:* In calculus, the differential represents a change in the linearization of a function....
dy is sometimes called the principal (linear) part of the function increment Δy.
Distribution theory
The term principal part is also used for certain kinds of distributionsDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
having a singular support at a single point.