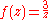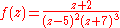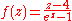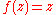Pole (complex analysis) - AbsoluteAstronomy.com

In the mathematical field of complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

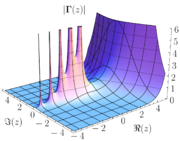
, a pole of a meromorphic function

Meromorphic function

In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...

is a certain type of singularity

Mathematical singularity

In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...

that behaves like the singularity of

at z = 0. This means that, in particular, a pole of the function f(z) is a point a such that f(z) approaches infinity as z approaches a.

Definition

Formally, suppose U is an open subset of the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

C, a is an element of U and f : U \ {a} → C is a function which is holomorphic over its domain. If there exists a holomorphic function g : U → C and a positive integer n, such that for all z in U \ {a}

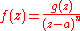
holds, then a is called a pole of f. The smallest such n is called the order of the pole. A pole of order 1 is called a simple pole.

A few authors allow the order of a pole to be zero, in which case a pole of order zero is either a regular point or a removable singularity. However, it is more usual to require the order of a pole to be positive.

From above several equivalent characterizations can be deduced:

If n is the order of pole a, then necessarily g(a) ≠ 0 for the function g in the above expression. So we can put

for some h that is holomorphic in an open neighborhood of a and has a zero of order n at a. So informally one might say that poles occur as reciprocals of zeros of holomorphic functions.

Also, by the holomorphy of g, f can be expressed as:

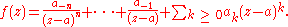
This is a Laurent series

Laurent series

In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...

with finite principal part. The holomorphic function

(on U) is called the regular part of f. So the point a is a pole of order n of f if and only if all the terms in the Laurent series expansion of f around a below degree −n vanish and the term in degree −n is not zero.

Pole at infinity

It can be defined for a complex function the notion of having a pole at the point at infinity. In this case U has to be a neighborhood of infinity. For example, the exterior of any closed ball. Now, for using the previous definition a meaning for g being holomorphic at ∞ should be given and also for the notion of "having" a zero at infinity as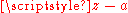

does at the finite point a. Instead a definition can be given starting from the definition at a finite point by "bringing" the point at infinity to a finite point. The map

does that. Then, by definition, a function, f, holomorphic in a neighborhood of infinity has a pole at infinity if the function

(which will be holomorphic in a neighborhood of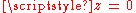

), has a pole at

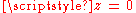, the order of which will be taken as the order of the pole at infinity.

Pole of a function on a complex manifold

In general, having a function

that is holomorphic in a neighborhood,

, of the point

, in the complex manifold

Complex manifold

In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....

M, it is said that f has a pole at a of order n if, having a chart

Atlas (topology)

In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...

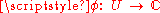, the function

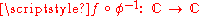has a pole of order n at

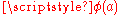(which can be taken as being zero if a convenient choice of the chart is made).
]
The pole at infinity is the simplest nontrivial example of this definition in which M is taken to be the Riemann sphere

Riemann sphere

In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...

and the chart is taken to be

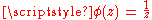Examples

The function

has a pole of order 1 or simple pole at

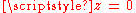The function

has a pole of order 2 at

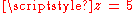and a pole of order 3 at

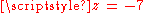The function

has poles of order 1 at

To see that, write

in Taylor series

Taylor series

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

around the origin.

The function

has a single pole at infinity of order 1.

Terminology and generalisations

If the first derivative of a function f has a simple pole at a, then a is a branch point

Branch point

In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that the function is discontinuous when going around an arbitrarily small circuit around this point...

of f. (The converse need not be true).

A non-removable singularity that is not a pole or a branch point

Branch point

is called an essential singularity

Essential singularity

In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...

.

A complex function which is holomorphic except for some isolated singularities and whose only singularities are poles is called meromorphic.

External links

Module for Zeros and Poles by John H. Mathews