
Filter (signal processing)
Encyclopedia
In signal processing
, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal. Most often, this means removing some frequencies
and not others in order to suppress interfering signals and reduce background noise. However, filters do not exclusively act in the frequency domain
; especially in the field of image processing
many other targets for filtering exist.
The drawback of filtering is the loss of information associated with it. Signal combination
in Fourier space is an alternative approach for removal of certain frequencies from the recorded signal.
There are many different bases of classifying filters and these overlap in many different ways; there is no simple hierarchical classification. Filters may be:
to remove certain frequencies
and allow others to pass. Such a filter is, of necessity, a linear filter
. Any non-linearity will result in the output signal containing components of frequency which were not present in the input signal.
The modern design methodology for linear continuous-time filters is called network synthesis
. Some important filter families designed in this way are:
The difference between these filter families is that they all use a different polynomial function to approximate to the ideal filter response. This results in each having a different transfer function
.
Another older, less-used methodology is the image parameter method
. Filters designed by this methodology are archaically called "wave filters". Some important filters designed by this method are:
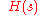 of a filter is the ratio of the output signal
of a filter is the ratio of the output signal 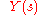 to that of the input signal
to that of the input signal 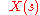 as a function of the complex frequency
as a function of the complex frequency  :
:
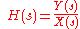
with .
.
The transfer function of all linear time-invariant filters generally share certain characteristics:
Distributed element filters do not, in general, produce rational functions but can often approximate to them.
The proper construction of a transfer function involves the Laplace transform, and therefore it is needed to assume null initial conditions, because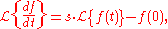
And when f(0)=0 we can get rid of the constants and use the usual expression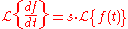
An alternative to transfer functions is to give the behavior of the filter as a convolution
. The convolution theorem
, which holds for Laplace transforms, guarantees equivalence with transfer functions.
Each family of filters can be specified to a particular order. The higher the order, the more the filter will approach the "ideal" filter; but also the longer the impulse response is and the longer the latency will be. An ideal filter has full transmission in the pass band, complete attenuation in the stop band, and an abrupt transition between the two bands, but this filter has infinite order (i.e., the response cannot be expressed as a linear differential equation
with a finite sum) and infinite latency (i.e., its compact support in the Fourier transform
forces its time response to be ever lasting).
Here is an image comparing Butterworth, Chebyshev, and elliptic filters. The filters in this illustration are all fifth-order low-pass filters. The particular implementation – analog or digital, passive or active – makes no difference; their output would be the same.
 As is clear from the image, elliptic filters are sharper than all the others, but they show ripples on the whole bandwidth.
As is clear from the image, elliptic filters are sharper than all the others, but they show ripples on the whole bandwidth.
Any family can be used to implement a particular bandform of which frequencies are transmitted, and which, outside the passband, are more or less attenuated. The transfer function completely specifies the behavior of a linear filter, but not the particular technology used to implement it. In other words, there are a number of different ways of achieving a particular transfer function when designing a circuit. A particular bandform of filter can be obtained by transformation of a prototype filter of that family.
structures invariably take on the form of a filter, that is, a network of non-dissipative elements. For instance, in a passive electronics implementation, this would likely take the form of a ladder topology of inductors and capacitors. The design of matching networks shares much in common with filters and the design invariably will have a filtering action as an incindental consequence. Although the prime purpose of a matching network is not to filter, it is often the case that both functions are combined in the same circuit. The need for impedance matching does not arise while signals are in the digital domain.
Similar comments can be made regarding power dividers and directional couplers
. When implemented in a distributed element format these devices can take the form of a distributed element filter
. There are four ports too be matched and widening the bandwidth requires filter-like structures to achieve this. The inverse is also true; distributed element filters can take the form of coupled lines.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal. Most often, this means removing some frequencies
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
and not others in order to suppress interfering signals and reduce background noise. However, filters do not exclusively act in the frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
; especially in the field of image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
many other targets for filtering exist.
The drawback of filtering is the loss of information associated with it. Signal combination
Noise reduction
Noise reduction is the process of removing noise from a signal.All recording devices, both analogue or digital, have traits which make them susceptible to noise...
in Fourier space is an alternative approach for removal of certain frequencies from the recorded signal.
There are many different bases of classifying filters and these overlap in many different ways; there is no simple hierarchical classification. Filters may be:
- analog or digitalDigital filterIn electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
- discrete-time (sampled) or continuous-time
- linearLinear filterLinear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
or non-linearNon-linear filterA nonlinear filter is a signal-processing device whose output is not a linear function of its input. Terminology concerning the filtering problem may refer to the time domain showing of the signal or to the frequency domain representation of the signal. When referring to filters with adjectives... - time-invariantTime-variant systemA time-variant system is a system that is not time invariant . Roughly speaking, characteristics of its output depend explicitly upon time.- Overview :...
or time-variantTime-variant systemA time-variant system is a system that is not time invariant . Roughly speaking, characteristics of its output depend explicitly upon time.- Overview :...
, also known as shift invariance. If the filter operates in a spatial domain then the characterization is space invariance. - passive or activeActive filterAn active filter is a type of analog electronic filter that uses an amplifier stage. Amplifiers included in a filter design can be used to improve the performance, stability and predictability of a filter. An amplifier prevents the impedance of source or load stages from affecting the...
type of continuous-time filter - infinite impulse responseInfinite impulse responseInfinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
(IIR) or finite impulse responseFinite impulse responseA finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
(FIR) type of discrete-time or digital filter.
Linear continuous-time filters
Linear continuous-time circuit is perhaps the most common meaning for filter in the signal processing world, and simply "filter" is often taken to be synonymous. These are filters that are designedFilter design
Filter design is the process of designing a filter , often a linear shift-invariant filter, that satisfies a set of requirements, some of which are contradictory...
to remove certain frequencies
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
and allow others to pass. Such a filter is, of necessity, a linear filter
Linear filter
Linear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
. Any non-linearity will result in the output signal containing components of frequency which were not present in the input signal.
The modern design methodology for linear continuous-time filters is called network synthesis
Network synthesis filters
Network synthesis is a method of designing signal processing filters. It has produced several important classes of filter including the Butterworth filter, the Chebyshev filter and the Elliptic filter. It was originally intended to be applied to the design of passive linear analogue filters but...
. Some important filter families designed in this way are:
- Chebyshev filterChebyshev filterChebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
, has the best approximation to the ideal response of any filter for a specified order and ripple. - Butterworth filterButterworth filterThe Butterworth filter is a type of signal processing filter designed to have as flat a frequency response as possible in the passband so that it is also termed a maximally flat magnitude filter...
, has a maximally flat frequency response. - Bessel filterBessel filterIn electronics and signal processing, a Bessel filter is a type of linear filter with a maximally flat group delay . Bessel filters are often used in audio crossover systems...
, has a maximally flat phase delay. - Elliptic filterElliptic filterAn elliptic filter is a signal processing filter with equalized ripple behavior in both the passband and the stopband...
, has the steepest cutoff of any filter for a specified order and ripple.
The difference between these filter families is that they all use a different polynomial function to approximate to the ideal filter response. This results in each having a different transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
.
Another older, less-used methodology is the image parameter method
Composite image filter
A composite image filter is an electronic filter consisting of multiple image filter sections of two or more different types.The image method of filter design determines the properties of filter sections by calculating the properties they have in an infinite chain of such sections. In this, the...
. Filters designed by this methodology are archaically called "wave filters". Some important filters designed by this method are:
- Constant k filterConstant k filterConstant k filters, also k-type filters, are a type of electronic filter designed using the image method. They are the original and simplest filters produced by this methodology and consist of a ladder network of identical sections of passive components...
, the original and simplest form of wave filter. - m-derived filterM-derived filterm-derived filters or m-type filters are a type of electronic filter designed using the image method. They were invented by Otto Zobel in the early 1920s. This filter type was originally intended for use with telephone multiplexing and was an improvement on the existing constant k type filter...
, a modification of the constant k with improved cutoff steepness and impedance matchingImpedance matchingIn electronics, impedance matching is the practice of designing the input impedance of an electrical load to maximize the power transfer and/or minimize reflections from the load....
.
Terminology
Some terms used to describe and classify linear filters:- The frequency response can be classified into a number of different bandforms describing which frequencies the filter passes (the passbandPassbandA passband is the range of frequencies or wavelengths that can pass through a filter without being attenuated.A bandpass filtered signal , is known as a bandpass signal, as opposed to a baseband signal....
) and which it rejects (the stopbandStopbandA stopband is a band of frequencies, between specified limits, through which a circuit, such as a filter or telephone circuit, does not allow signals to pass, or the attenuation is above the required stopband attenuation level...
):- Low-pass filterLow-pass filterA low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
– low frequencies are passed, high frequencies are attenuated. - High-pass filterHigh-pass filterA high-pass filter is a device that passes high frequencies and attenuates frequencies lower than its cutoff frequency. A high-pass filter is usually modeled as a linear time-invariant system...
– high frequencies are passed, low frequencies are attenuated. - Band-pass filterBand-pass filterA band-pass filter is a device that passes frequencies within a certain range and rejects frequencies outside that range.Optical band-pass filters are of common usage....
– only frequencies in a frequency band are passed. - Band-stop filterBand-stop filterIn signal processing, a band-stop filter or band-rejection filter is a filter that passes most frequencies unaltered, but attenuates those in a specific range to very low levels. It is the opposite of a band-pass filter...
or band-reject filter – only frequencies in a frequency band are attenuated. - Notch filter – rejects just one specific frequency - an extreme band-stop filter.
- Comb filterComb filterIn signal processing, a comb filter adds a delayed version of a signal to itself, causing constructive and destructive interference. The frequency response of a comb filter consists of a series of regularly spaced spikes, giving the appearance of a comb....
– has multiple regularly spaced narrow passbands giving the bandform the appearance of a comb. - All-pass filterAll-pass filterAn all-pass filter is a signal processing filter that passes all frequencies equally, but changes the phase relationship between various frequencies. It does this by varying its propagation delay with frequency...
– all frequencies are passed, but the phase of the output is modified.
- Low-pass filter
- Cutoff frequencyCutoff frequencyIn physics and electrical engineering, a cutoff frequency, corner frequency, or break frequency is a boundary in a system's frequency response at which energy flowing through the system begins to be reduced rather than passing through.Typically in electronic systems such as filters and...
is the frequency beyond which the filter will not pass signals. It is usually measured at a specific attenuation such as 3dB. - Roll-offRoll-offRoll-off is a term commonly used to describe the steepness of a transmission function with frequency, particularly in electrical network analysis, and most especially in connection with filter circuits in the transition between a passband and a stopband...
is the rate at which attenuation increases beyond the cut-off frequency. - Transition bandTransition bandThe transition band is a range of frequencies, that allows a transition between a passband and a stopband of a signal processing filter. The transition band is defined by a passband and a stopband cutoff frequency or corner frequency....
, the (usually narrow) band of frequencies between a passband and stopband. - Ripple is the variation of the filters insertion lossInsertion lossIn telecommunications, insertion loss is the loss of signal power resulting from the insertion of a device in a transmission line or optical fiber and is usually expressed in decibels ....
in the passband. - The order of a filter is the degree of the approximating polynomialDegree of a polynomialThe degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
and in passive filters corresponds to the number of elements required to build it. Increasing order increases roll-off and brings the filter closer to the ideal response.
Technologies
Filters can be built in a number of different technologies. The same transfer function can be realised in several different ways, that is the mathematical properties of the filter are the same but the physical properties are quite different. Often the components in different technologies are directly analogous to each other and fulfill the same role in their respective filters. For instance, the resistors, inductors and capacitors of electronics correspond respectively to dampers, masses and springs in mechanics. Likewise, there are corresponding components in distributed element filters.- Electronic filterElectronic filterElectronic filters are electronic circuits which perform signal processing functions, specifically to remove unwanted frequency components from the signal, to enhance wanted ones, or both...
s were originally entirely passive consisting of resistance, inductance and capacitance. Active technology makes design easier and opens up new possibilities in filter specifications. - Digital filterDigital filterIn electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
s operate on signals represented in digital form. The essence of a digital filter is that it directly implements a mathematical algorithm, corresponding to the desired filter transfer function, in its programming or microcode. - Mechanical filterMechanical filterA mechanical filter is a signal processing filter usually used in place of an electronic filter at radio frequencies. Its purpose is the same as that of a normal electronic filter: to pass a range of signal frequencies, but to block others. The filter acts on mechanical vibrations which are the...
s are built out of mechanical components. In the vast majority of cases they are used to process an electronic signal and transducerTransducerA transducer is a device that converts one type of energy to another. Energy types include electrical, mechanical, electromagnetic , chemical, acoustic or thermal energy. While the term transducer commonly implies the use of a sensor/detector, any device which converts energy can be considered a...
s are provided to convert this to and from a mechanical vibration. However, examples do exist of filters that have been designed for operation entirely in the mechanical domain. - Distributed element filterDistributed element filterA distributed element filter is an electronic filter in which capacitance, inductance and resistance are not localised in discrete capacitors, inductors and resistors as they are in conventional filters. Its purpose is to allow a range of signal frequencies to pass, but to block others...
s are constructed out of components made from small pieces of transmission lineTransmission lineIn communications and electronic engineering, a transmission line is a specialized cable designed to carry alternating current of radio frequency, that is, currents with a frequency high enough that its wave nature must be taken into account...
or other distributed elementsDistributed element modelIn electrical engineering, the distributed element model or transmission line model of electrical circuits assumes that the attributes of the circuit are distributed continuously throughout the material of the circuit...
. There are structures in distributed element filters that directly correspond to the lumped elementsLumped element modelThe lumped element model simplifies the description of the behaviour of spatially distributed physical systems into a topology consisting of discrete entities that approximate the behaviour of the distributed system under certain assumptions...
of electronic filters, and others that are unique to this class of technology. - Waveguide filters consist of waveguide components or components inserted in the waveguide. Waveguides are a class of transmission line and many structures of distributed element filters, for instance the stub (electronics), can be implemented in waveguides also.
- Acoustic filters
- Optical filterFilter (optics)Optical filters are devices which selectively transmit light of different wavelengths, usually implemented as plane glass or plastic devices in the optical path which are either dyed in the mass or have interference coatings....
s were originally developed for purposes other than signal processing such as lighting and photography. With the rise of optical fiberOptical fiberAn optical fiber is a flexible, transparent fiber made of a pure glass not much wider than a human hair. It functions as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of...
technology, however, optical filters increasingly find signal processing applications and signal processing filter terminology, such as longpass and shortpass, are entering the field.
The transfer function
The transfer functionTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
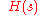 of a filter is the ratio of the output signal
of a filter is the ratio of the output signal 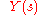 to that of the input signal
to that of the input signal 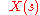 as a function of the complex frequency
as a function of the complex frequency  :
: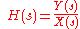
with
 .
.The transfer function of all linear time-invariant filters generally share certain characteristics:
- For filters which are constructed of discrete components, their transfer function must be the ratio of two polynomials in
 , i.e. a rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
, i.e. a rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of . The order of the transfer function will be the highest power of
. The order of the transfer function will be the highest power of  encountered in either the numerator or the denominator.
encountered in either the numerator or the denominator. - The polynomials of the transfer function will all have real coefficients. Therefore, the poles and zeroes of the transfer function will either be real or occur in complex conjugate pairs.
- Since the filters are assumed to be stable, the real part of all poles (i.e. zeroes of the denominator) will be negative, i.e. they will lie in the left half-plane in complex frequency space.
Distributed element filters do not, in general, produce rational functions but can often approximate to them.
The proper construction of a transfer function involves the Laplace transform, and therefore it is needed to assume null initial conditions, because
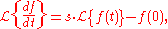
And when f(0)=0 we can get rid of the constants and use the usual expression
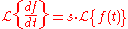
An alternative to transfer functions is to give the behavior of the filter as a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
. The convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
, which holds for Laplace transforms, guarantees equivalence with transfer functions.
Classification
Filters may be specified by family and bandform. A filter's family is specified by the approximating polynomial used and each leads to certain characteristics of the transfer function of the filter. Some common filter families and their particular characteristics are:- Butterworth filterButterworth filterThe Butterworth filter is a type of signal processing filter designed to have as flat a frequency response as possible in the passband so that it is also termed a maximally flat magnitude filter...
– no gain ripple in pass band and stop band, slow cutoff - Chebyshev filter (Type I)Chebyshev filterChebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
– no gain ripple in stop band, moderate cutoff - Chebyshev filter (Type II)Chebyshev filterChebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
– no gain ripple in pass band, moderate cutoff - Bessel filterBessel filterIn electronics and signal processing, a Bessel filter is a type of linear filter with a maximally flat group delay . Bessel filters are often used in audio crossover systems...
– no group delayGroup delayGroup delay is a measure of the time delay of the amplitude envelopes of the various sinusoidal components of a signal through a device under test, and is a function of frequency for each component...
ripple, no gain ripple in both bands, slow gain cutoff - Elliptic filterElliptic filterAn elliptic filter is a signal processing filter with equalized ripple behavior in both the passband and the stopband...
– gain ripple in pass and stop band, fast cutoff - Optimum "L" filter
- Gaussian filterGaussian filterIn electronics and signal processing, a Gaussian filter is a filter whose impulse response is a Gaussian function. Gaussian filters are designed to give no overshoot to a step function input while minimizing the rise and fall time. This behavior is closely connected to the fact that the Gaussian...
– no ripple in response to step function - Hourglass filter
- Raised-cosine filterRaised-cosine filterThe raised-cosine filter is a filter frequently used for pulse-shaping in digital modulation due to its ability to minimise intersymbol interference...
Each family of filters can be specified to a particular order. The higher the order, the more the filter will approach the "ideal" filter; but also the longer the impulse response is and the longer the latency will be. An ideal filter has full transmission in the pass band, complete attenuation in the stop band, and an abrupt transition between the two bands, but this filter has infinite order (i.e., the response cannot be expressed as a linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
with a finite sum) and infinite latency (i.e., its compact support in the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
forces its time response to be ever lasting).
Here is an image comparing Butterworth, Chebyshev, and elliptic filters. The filters in this illustration are all fifth-order low-pass filters. The particular implementation – analog or digital, passive or active – makes no difference; their output would be the same.

Any family can be used to implement a particular bandform of which frequencies are transmitted, and which, outside the passband, are more or less attenuated. The transfer function completely specifies the behavior of a linear filter, but not the particular technology used to implement it. In other words, there are a number of different ways of achieving a particular transfer function when designing a circuit. A particular bandform of filter can be obtained by transformation of a prototype filter of that family.
Impedance matching
Impedance matchingImpedance matching
In electronics, impedance matching is the practice of designing the input impedance of an electrical load to maximize the power transfer and/or minimize reflections from the load....
structures invariably take on the form of a filter, that is, a network of non-dissipative elements. For instance, in a passive electronics implementation, this would likely take the form of a ladder topology of inductors and capacitors. The design of matching networks shares much in common with filters and the design invariably will have a filtering action as an incindental consequence. Although the prime purpose of a matching network is not to filter, it is often the case that both functions are combined in the same circuit. The need for impedance matching does not arise while signals are in the digital domain.
Similar comments can be made regarding power dividers and directional couplers
Power dividers and directional couplers
Power dividers and directional couplers are passive devices used in the field of radio technology. They couple a defined amount of the electromagnetic power in a transmission line to another port where it can be used in another circuit...
. When implemented in a distributed element format these devices can take the form of a distributed element filter
Distributed element filter
A distributed element filter is an electronic filter in which capacitance, inductance and resistance are not localised in discrete capacitors, inductors and resistors as they are in conventional filters. Its purpose is to allow a range of signal frequencies to pass, but to block others...
. There are four ports too be matched and widening the bandwidth requires filter-like structures to achieve this. The inverse is also true; distributed element filters can take the form of coupled lines.
Filters for removing noise from data
- Wiener filterWiener filterIn signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
- Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
- Savitzky–Golay smoothing filterSavitzky–Golay smoothing filterThe Savitzky–Golay smoothing filter is a type of filter first described in 1964 by Abraham Savitzky and Marcel J. E. Golay.The Savitzky–Golay method essentially performs a local polynomial regression on a series of values to determine the smoothed value for each point...

