Comb filter
Encyclopedia
In signal processing
, a comb filter adds a delayed version of a signal
to itself, causing constructive and destructive interference. The frequency response
of a comb filter consists of a series of regularly spaced spikes, giving the appearance of a comb
.
In acoustics
, comb filtering can arise in some unwanted ways. For instance, when two loudspeakers are playing the same signal at different distances from the listener, there is a comb filtering effect on the signal. In any enclosed space, listeners hear a mixture of direct sound and reflected sound. Because the reflected sound takes a longer path, it constitutes a delayed version of the direct sound and a comb filter is created where the two combine at the listener.
and feedback
; the names refer to the direction in which signals are delayed before they are added to the input.
Comb filters may be implemented in discrete time
or continuous time; this article will focus on discrete-time implementations; the properties of the continuous-time comb filter are very similar.
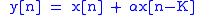
where
is the delay length (measured in samples), and 
is a scaling factor applied to the delayed signal. If we take the Z transform of both sides of the equation, we obtain:
We define the transfer function as: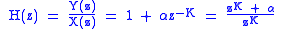
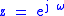. Therefore, for our feedforward comb filter, we get: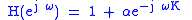
Using Euler's formula
, we find that the frequency response is also given by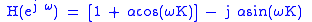
Often of interest is the magnitude response, which ignores phase. This is defined as: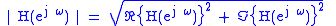
In the case of the feedforward comb filter, this is:
Notice that the
term is constant, whereas the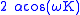 
term varies periodically
. Hence the magnitude response of the comb filter is periodic.
The graphs to the right show the magnitude response for various values of
, demonstrating this periodicity. Some important properties:
filters. Its response is simply the initial impulse with a second impulse after the delay.
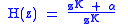
we see that the numerator is equal to zero whenever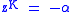
. This has 
solutions, equally spaced around a circle in the complex plane
; these are the zeros
of the transfer function. The denominator is zero at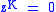
, giving 
poles at 
. This leads to a pole-zero plot
like the ones shown below.
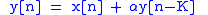
If we rearrange this equation so that all terms in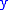
are on the left-hand side, and then take the Z transform, we obtain: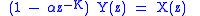
The transfer function is therefore: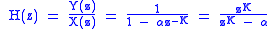
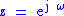into the Z-domain expression for the feedback comb filter, we get: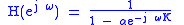
The magnitude response is as follows: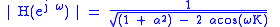
Again, the response is periodic, as the graphs to the right demonstrate. The feedback comb filter has some properties in common with the feedforward form:
However, there are also some important differences because the magnitude response has a term in the denominator:
filter. If stable, the response simply consists of a repeating series of impulses decreasing in amplitude over time.
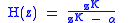
This time, the numerator is zero at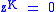
, giving 
zeros at 
. The denominator is equal to zero whenever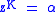 
. This has 
solutions, equally spaced around a circle in the complex plane
; these are the poles of the transfer function. This leads to a pole-zero plot like the ones shown below.
and the feedback form by:
where
is the delay (measured in seconds).
They have the following frequency responses, respectively: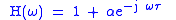
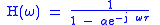
Continuous-time implementations share all the properties of the respective discrete-time implementations.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, a comb filter adds a delayed version of a signal
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
to itself, causing constructive and destructive interference. The frequency response
Frequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
of a comb filter consists of a series of regularly spaced spikes, giving the appearance of a comb
Comb
A comb is a toothed device used in hair care for straightening and cleaning hair or other fibres. Combs are among the oldest tools found by archaeologists...
.
Applications
Comb filters are used in a variety of signal processing applications. These include:- Cascaded Integrator-CombCascaded Integrator-Comb FilterIn digital signal processing, a cascaded integrator-comb is an optimized class of finite impulse response filter combined with an interpolator or decimator.A CIC filter consists of one or more integrator and comb filter pairs...
(CIC) filters, commonly used for anti-aliasingAnti-aliasingIn digital signal processing, spatial anti-aliasing is the technique of minimizing the distortion artifacts known as aliasing when representing a high-resolution image at a lower resolution...
during interpolationInterpolationIn the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
and decimationDecimation (signal processing)In digital signal processing, decimation is a technique for reducing the number of samples in a discrete-time signal. The element which implements this technique is referred to as a decimator.Decimation is a two-step process:...
operations that change the sample rate of a discrete-time system. - 2D and 3D comb filters implemented in hardware (and occasionally software) for PALPALPAL, short for Phase Alternating Line, is an analogue television colour encoding system used in broadcast television systems in many countries. Other common analogue television systems are NTSC and SECAM. This page primarily discusses the PAL colour encoding system...
and NTSCNTSCNTSC, named for the National Television System Committee, is the analog television system that is used in most of North America, most of South America , Burma, South Korea, Taiwan, Japan, the Philippines, and some Pacific island nations and territories .Most countries using the NTSC standard, as...
television decoders. The filters work to reduce artifacts such as dot crawlDot crawlDot crawl is the popular name for a visual defect of color analog video standards when signals are transmitted as composite video, as in terrestrial broadcast television. It consists of animated checkerboard patterns which appear along vertical color transitions...
. - Audio effects, including echoEcho (phenomenon)In audio signal processing and acoustics, an echo is a reflection of sound, arriving at the listener some time after the direct sound. Typical examples are the echo produced by the bottom of a well, by a building, or by the walls of an enclosed room and an empty room. A true echo is a single...
, flangingFlangingFlanging is an audio effect produced by mixing two identical signals together, with one signal delayed by a small and gradually changing period, usually smaller than 20 milliseconds. This produces a swept comb filter effect: peaks and notches are produced in the resultant frequency spectrum,...
, and digital waveguide synthesisDigital waveguide synthesisDigital waveguide synthesis is the synthesis of audio using a digital waveguide. Digital waveguides are efficient computational models for physical media through which acoustic waves propagate...
. For instance, if the delay is set to a few milliseconds, a comb filter can be used to model the effect of acousticAcousticsAcoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
standing waves in a cylindrical cavity or in a vibrating stringKarplus-Strong string synthesisKarplus-Strong string synthesis is a method of physical modelling synthesis that loops a short waveform through a filtered delay line to simulate the sound of a hammered or plucked string or some types of percussion....
.
In acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
, comb filtering can arise in some unwanted ways. For instance, when two loudspeakers are playing the same signal at different distances from the listener, there is a comb filtering effect on the signal. In any enclosed space, listeners hear a mixture of direct sound and reflected sound. Because the reflected sound takes a longer path, it constitutes a delayed version of the direct sound and a comb filter is created where the two combine at the listener.
Technical discussion
Comb filters exist in two different forms, feed-forwardFeed-forward
Feed-forward is a term describing an element or pathway within a control system which passes a controlling signal from a source in the control system's external environment, often a command signal from an external operator, to a load elsewhere in its external environment...
and feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
; the names refer to the direction in which signals are delayed before they are added to the input.
Comb filters may be implemented in discrete time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
or continuous time; this article will focus on discrete-time implementations; the properties of the continuous-time comb filter are very similar.
Feedforward form
The general structure of a feedforward comb filter is shown on the right. It may be described by the following difference equation: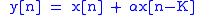where
is the delay length (measured in samples), and is a scaling factor applied to the delayed signal. If we take the Z transform of both sides of the equation, we obtain:We define the transfer function as:
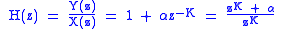
Frequency response
To obtain the frequency response of a discrete-time system expressed in the Z domain, we make the substitution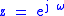. Therefore, for our feedforward comb filter, we get: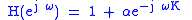Using Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
, we find that the frequency response is also given by
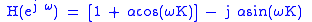
Often of interest is the magnitude response, which ignores phase. This is defined as:
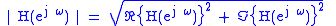
In the case of the feedforward comb filter, this is:
Notice that the
term is constant, whereas the 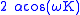term varies periodicallyPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
. Hence the magnitude response of the comb filter is periodic.
The graphs to the right show the magnitude response for various values of
, demonstrating this periodicity. Some important properties:
- The response periodically drops to a local minimum (sometimes known as a notch), and periodically rises to a local maximum (sometimes known as a peak).
- For positive values of
, the first minimum occurs at half the delay period and repeat at even multiples of the delay frequency thereafter: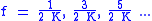 
. - The levels of the maxima and minima are always equidistant from 1.
- When
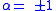, the minima have zero amplitude. In this case, the minima are sometimes known as nulls. - The maxima for positive values of
coincide with the minima for negative values of 
, and vice versa.
Impulse response
The feedforward comb filter is one of the simplest finite impulse responseFinite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
filters. Its response is simply the initial impulse with a second impulse after the delay.
Pole-zero interpretation
Looking again at the Z-domain transfer function of the feedforward comb filter: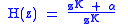we see that the numerator is equal to zero whenever
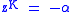. This has solutions, equally spaced around a circle in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
; these are the zeros
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
of the transfer function. The denominator is zero at
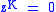, giving poles at . This leads to a pole-zero plotPole-zero plot
In mathematics, signal processing and control theory, a pole–zero plot is a graphical representation of a rational transfer function in the complex plane which helps to convey certain properties of the system such as:* Stability...
like the ones shown below.
Feedback form
Similarly, the general structure of a feedback comb filter is shown on the right. It may be described by the following difference equation: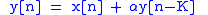If we rearrange this equation so that all terms in
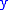are on the left-hand side, and then take the Z transform, we obtain: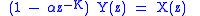The transfer function is therefore:
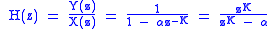
Frequency response
If we make the substitution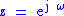 into the Z-domain expression for the feedback comb filter, we get: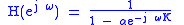The magnitude response is as follows:
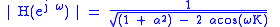
Again, the response is periodic, as the graphs to the right demonstrate. The feedback comb filter has some properties in common with the feedforward form:
- The response periodically drops to a local minimum and rises to a local maximum.
- The maxima for positive values of
coincide with the minima for negative values of 
, and vice versa. - For positive values of
, the first minimum occurs at 0 and repeats at even multiples of the delay frequency thereafter: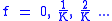 
.
However, there are also some important differences because the magnitude response has a term in the denominator:
- The levels of the maxima and minima are no longer equidistant from 1.
- The filter is only stableBIBO stabilityIn electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
if
is strictly less than 1. As can be seen from the graphs, as 
increases, the amplitude of the maxima rises increasingly rapidly.
Impulse response
The feedback comb filter is a simple type of infinite impulse responseInfinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
filter. If stable, the response simply consists of a repeating series of impulses decreasing in amplitude over time.
Pole-zero interpretation
Looking again at the Z-domain transfer function of the feedback comb filter: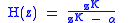This time, the numerator is zero at
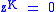, giving zeros at . The denominator is equal to zero whenever 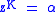. This has solutions, equally spaced around a circle in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
; these are the poles of the transfer function. This leads to a pole-zero plot like the ones shown below.
Continuous-time comb filters
Comb filters may also be implemented in continuous time. The feedforward form may be described by the following equation:and the feedback form by:
where
is the delay (measured in seconds).They have the following frequency responses, respectively:
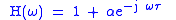
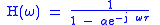
Continuous-time implementations share all the properties of the respective discrete-time implementations.