Cascaded Integrator-Comb Filter
Encyclopedia
In digital signal processing
, a cascaded integrator-comb (CIC) is an optimized class of finite impulse response
filter combined with an interpolator
or decimator
.
A CIC filter consists of one or more integrator
and comb filter
pairs. In the case of a decimating CIC, the input signal is fed through one or more cascaded integrators, then a down-sampler, followed by one or more comb sections (equal in number to the number of integrators). An interpolating CIC is simply the reverse of this architecture, with the down-sampler replaced with a zero-stuffer (up-sampler).
CIC filters were invented by Eugene B. Hogenauer, and are a class of FIR filters used in multi-rate processing
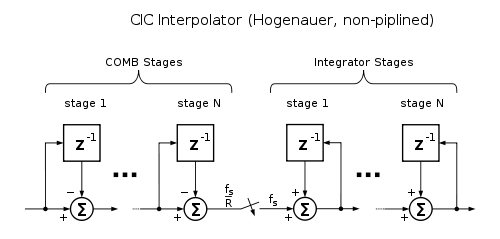
. The CIC filter finds applications in interpolation and decimation. Unlike most FIR filters, it has a decimator or interpolator built into the architecture. The figure at the right shows the Hogenauer architecture for a CIC Interpolator.
The system function for the composite CIC filter referenced to the high sampling rate, fs is:
Where:
Characteristics of CIC Filters
to the previous result 
and subtracting the oldest sample. Omitting the division by 
, we have:
The second equality corresponds to a comb (
) followed by an integrator (
). The conventional CIC structure is obtained by cascading 
identical moving average filters, then rearranging the sections to place all integrators first (decimator) or combs first (interpolator). Such rearrangement is possible because both combs and integrators are LTI
. For an interpolator, the upsampler which normally precedes the interpolation filter can be passed through the comb sections using a Noble identity, reducing the number of delay elements needed by a factor of
. Similarly, for a decimator, the downsampler which normally follows the decimation filter can be moved before the comb sections.
The equivalence of a CIC to moving average filter allows us to trivially calculate its bit growth as
.
, while low pass FIR filters can have an arbitrarily sharp frequency roll-off.
CIC filters are in general much more economical than general FIR filters, but tradeoffs are involved. In cases where only a small amount of interpolation or decimation are needed, FIR filters generally have the advantage. However, when rates change by a factor of 10 or more, achieving a useful FIR filter anti-aliasing stop band requires exponentially increasing numbers of FIR taps.
For large rate changes, a CIC has a significant advantage over a FIR filter with respect to architectural and computational efficiency. Additionally, CIC filters can typically be reconfigured for different rates by changing nothing more than the decimation/interpolation section assuming the bit width of the integrators and comb sections meets certain mathematical criteria based on the maximum possible rate change.
Whereas a FIR filter can use fixed
or floating point
math, a CIC filter uses only fixed point math. This is necessary because, as a recursively implemented FIR filter, a CIC filter relies on exact cancellation of poles from the integrator sections by zeros from the comb sections. While the reasons are less than intuitive, an inherent characteristic of the CIC architecture is that if fixed bit length overflow
s occur in the integrators, they are corrected in the comb sections.
The range of filter shapes and responses available from a CIC filter is somewhat limited. Larger amounts of stopband
rejection can be achieved by increasing the number of poles. However, doing so requires an increase in bit width in the integrator and comb sections which increases filter complexity
. The shape of the filter response provides even fewer degrees of design freedom. For this reason, many real-world filtering requirements cannot be met by a CIC filter alone. However, a CIC filter followed by a short to moderate length FIR or IIR proves highly applicable. Additionally, the FIR filter shape is normalized relative to the CIC's sampling rate at the FIR/CIC interface so one set of FIR coefficients can be used over a range of CIC interpolation and decimation rates.
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
, a cascaded integrator-comb (CIC) is an optimized class of finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
filter combined with an interpolator
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
or decimator
Decimation (signal processing)
In digital signal processing, decimation is a technique for reducing the number of samples in a discrete-time signal. The element which implements this technique is referred to as a decimator.Decimation is a two-step process:...
.
A CIC filter consists of one or more integrator
Integrator
An integrator is a device to perform the mathematical operation known as integration, a fundamental operation in calculus.The integration function is often part of engineering, physics, mechanical, chemical and scientific calculations....
and comb filter
Comb filter
In signal processing, a comb filter adds a delayed version of a signal to itself, causing constructive and destructive interference. The frequency response of a comb filter consists of a series of regularly spaced spikes, giving the appearance of a comb....
pairs. In the case of a decimating CIC, the input signal is fed through one or more cascaded integrators, then a down-sampler, followed by one or more comb sections (equal in number to the number of integrators). An interpolating CIC is simply the reverse of this architecture, with the down-sampler replaced with a zero-stuffer (up-sampler).
The CIC filter
Multi-rate digital signal processing
Multi-rate signal processing studies digital signal processing systems which include sample rate conversion. Multirate signal processing techniques are necessary for systems with different input and output sample rates, but may also be used to implement systems with equal input and output rates.-...
. The CIC filter finds applications in interpolation and decimation. Unlike most FIR filters, it has a decimator or interpolator built into the architecture. The figure at the right shows the Hogenauer architecture for a CIC Interpolator.
The system function for the composite CIC filter referenced to the high sampling rate, fs is:
Where:
- R = decimation or interpolation ratio
- M = number of samples per stage (usually 1 but sometimes 2)
- N = number of stages in filter
Characteristics of CIC Filters
- Linear phase response;
- Utilize only delay and addition and subtraction; that is, it requires no multiplication operations;
CIC as a moving average filter
A CIC filter is an efficient implementation of a moving average filter. To see this, consider how a moving average filter can be implemented recursively by adding the newest sample to the previous result and subtracting the oldest sample. Omitting the division by , we have:The second equality corresponds to a comb (
) followed by an integrator (). The conventional CIC structure is obtained by cascading identical moving average filters, then rearranging the sections to place all integrators first (decimator) or combs first (interpolator). Such rearrangement is possible because both combs and integrators are LTILTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
. For an interpolator, the upsampler which normally precedes the interpolation filter can be passed through the comb sections using a Noble identity, reducing the number of delay elements needed by a factor of
. Similarly, for a decimator, the downsampler which normally follows the decimation filter can be moved before the comb sections.The equivalence of a CIC to moving average filter allows us to trivially calculate its bit growth as
.Comparison with other filters
CIC filters are used in multi-rate processing. An FIR filter is used in a wide array of applications, and can be used in multi-rate processing in conjunction with an interpolator or decimator. CIC filters have low pass frequency characteristics, while FIR filters can have low-pass, high-pass, or band-pass frequency characteristics. CIC filters use only addition and subtraction. FIR filters use addition, subtraction, but most FIR filters also require multiplication. CIC filters have a specific frequency roll-offRoll-off
Roll-off is a term commonly used to describe the steepness of a transmission function with frequency, particularly in electrical network analysis, and most especially in connection with filter circuits in the transition between a passband and a stopband...
, while low pass FIR filters can have an arbitrarily sharp frequency roll-off.
CIC filters are in general much more economical than general FIR filters, but tradeoffs are involved. In cases where only a small amount of interpolation or decimation are needed, FIR filters generally have the advantage. However, when rates change by a factor of 10 or more, achieving a useful FIR filter anti-aliasing stop band requires exponentially increasing numbers of FIR taps.
For large rate changes, a CIC has a significant advantage over a FIR filter with respect to architectural and computational efficiency. Additionally, CIC filters can typically be reconfigured for different rates by changing nothing more than the decimation/interpolation section assuming the bit width of the integrators and comb sections meets certain mathematical criteria based on the maximum possible rate change.
Whereas a FIR filter can use fixed
Fixed-point arithmetic
In computing, a fixed-point number representation is a real data type for a number that has a fixed number of digits after the radix point...
or floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
math, a CIC filter uses only fixed point math. This is necessary because, as a recursively implemented FIR filter, a CIC filter relies on exact cancellation of poles from the integrator sections by zeros from the comb sections. While the reasons are less than intuitive, an inherent characteristic of the CIC architecture is that if fixed bit length overflow
Arithmetic overflow
The term arithmetic overflow or simply overflow has the following meanings.# In a computer, the condition that occurs when a calculation produces a result that is greater in magnitude than that which a given register or storage location can store or represent.# In a computer, the amount by which a...
s occur in the integrators, they are corrected in the comb sections.
The range of filter shapes and responses available from a CIC filter is somewhat limited. Larger amounts of stopband
Stopband
A stopband is a band of frequencies, between specified limits, through which a circuit, such as a filter or telephone circuit, does not allow signals to pass, or the attenuation is above the required stopband attenuation level...
rejection can be achieved by increasing the number of poles. However, doing so requires an increase in bit width in the integrator and comb sections which increases filter complexity
Complexity
In general usage, complexity tends to be used to characterize something with many parts in intricate arrangement. The study of these complex linkages is the main goal of complex systems theory. In science there are at this time a number of approaches to characterizing complexity, many of which are...
. The shape of the filter response provides even fewer degrees of design freedom. For this reason, many real-world filtering requirements cannot be met by a CIC filter alone. However, a CIC filter followed by a short to moderate length FIR or IIR proves highly applicable. Additionally, the FIR filter shape is normalized relative to the CIC's sampling rate at the FIR/CIC interface so one set of FIR coefficients can be used over a range of CIC interpolation and decimation rates.