Karplus-Strong string synthesis
Encyclopedia
Karplus-Strong string synthesis is a method of physical modelling synthesis
that loops a short waveform through a filtered delay line to simulate the sound of a hammered or plucked string
or some types of percussion
.
Although it is useful to view this as a subtractive synthesis
technique based on a feedback loop similar to that of a comb filter
for z-transform
analysis, it is better viewed as the simplest of a class of wavetable-modification algorithms now known as digital waveguide synthesis
, as the delay line acts to store one period of the signal.
Alexander Strong invented the algorithm, and Kevin Karplus
did the first analysis of how it worked. Together they developed software and hardware implementations of the algorithm, including a custom VLSI chip. They named the algorithm "Digitar" synthesis, as an abbreviation for "digital guitar".
(specifically, the lowest nonzero resonant frequency) of the resulting signal is the lowest frequency at which the unwrapped phase response of the delay and filter in cascade is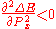
. The required phase delay D for a given fundamental frequency F0 is therefore calculated according to D = Fs/F0 where Fs is the sampling frequency.
The length of any digital delay line is a whole-number multiple of the sampling period. In order to obtain a fractional delay, interpolating filters
are used with parameters selected to obtain an appropriate phase delay at the fundamental frequency. Either IIR
or FIR
filters may be used, however FIR have the advantage that transients are suppressed if the fractional delay is changed over time. The most elementary fractional delay is the linear interpolation
between two samples (e.g., s(4.2) = 0.8s(4) + 0.2s(5)). If the phase delay varies with frequency, harmonic
s may be sharpened or flattened relative to the fundamental frequency. The original algorithm used equal weighting on two adjacent samples, as this can be achieved without multiplication hardware, allowing extremely cheap implementations.
Z-transform
analysis can be used to get the pitches and decay times of the harmonics more precisely, as explained in the 1983 paper that introduced the algorithm.
A demonstration of the Karplus-Strong algorithm can be heard in the following Vorbis
file. The algorithm used a loop gain of 0.98 with increasingly attenuating first order lowpass filters. The pitch of the note was A2, or 220 Hz.
Holding the period (= length of the delay line) constant produces vibrations similar to those of a string or bell. Increasing the period sharply after the transient input produces drum-like sounds.
realized that the Karplus-Strong algorithm was physically analogous to a sampling of the transversal wave on a string instrument, with the filter in the feedback loop representing the total string losses over one period. Julius O. Smith III http://ccrma.stanford.edu/~jos/ and others
generalized the algorithm to digital waveguide synthesis
, which could also be used to model acoustic waves in tubes and on drum membranes.
Alex Strong developed a superior wavetable-modification method for plucked-string synthesis, but only published it as a patent.
, and scored for eight guitars, mezzo-soprano and computer-generated stereo tape, with a text based on Carl Sandburg
's The People, Yes. Jaffe continued to explore the musical and technical possibilities of the algorithm in Silicon Valley Breakdown, for computer-generated plucked strings (1982), as well as in later works such as Telegram to the President, 1984 for string quartet and tape, and Grass for female chorus and tape (1987).
The patent was licensed first to Mattel Electronics, which failed as a company before any product using the algorithm was developed, then to a startup company founded by some of the laid-off Mattel executives. They never got sufficient funding to finish development, and so never brought a product to market either. Eventually Yamaha licensed the patent, as part of the Sondius package of patents from Stanford. It is unknown whether any hardware using the algorithm was ever sold, though many software implementations (which did not pay any license fees to the inventors) have been released.
Physical modelling synthesis
In sound synthesis, physical modelling synthesis refers to methods in which the waveform of the sound to be generated is computed by using a mathematical model, being a set of equations and algorithms to simulate a physical source of sound, usually a musical instrument...
that loops a short waveform through a filtered delay line to simulate the sound of a hammered or plucked string
String instrument
A string instrument is a musical instrument that produces sound by means of vibrating strings. In the Hornbostel-Sachs scheme of musical instrument classification, used in organology, they are called chordophones...
or some types of percussion
Percussion instrument
A percussion instrument is any object which produces a sound when hit with an implement or when it is shaken, rubbed, scraped, or otherwise acted upon in a way that sets the object into vibration...
.
Although it is useful to view this as a subtractive synthesis
Subtractive synthesis
Subtractive synthesis is a method of sound synthesis in which partials of an audio signal are attenuated by a filter to alter the timbre of the sound...
technique based on a feedback loop similar to that of a comb filter
Comb filter
In signal processing, a comb filter adds a delayed version of a signal to itself, causing constructive and destructive interference. The frequency response of a comb filter consists of a series of regularly spaced spikes, giving the appearance of a comb....
for z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
analysis, it is better viewed as the simplest of a class of wavetable-modification algorithms now known as digital waveguide synthesis
Digital waveguide synthesis
Digital waveguide synthesis is the synthesis of audio using a digital waveguide. Digital waveguides are efficient computational models for physical media through which acoustic waves propagate...
, as the delay line acts to store one period of the signal.
Alexander Strong invented the algorithm, and Kevin Karplus
Kevin Karplus
Kevin Karplus is a professor at University of California, Santa Cruz, currently in the Biomolecular Engineering Department.He is probably best known for work he did as a computer science graduate student at Stanford University on the Karplus-Strong string synthesis algorithm.He taught VLSI design...
did the first analysis of how it worked. Together they developed software and hardware implementations of the algorithm, including a custom VLSI chip. They named the algorithm "Digitar" synthesis, as an abbreviation for "digital guitar".
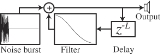
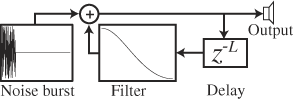
How it works
- A short excitation waveform (of length L samples) is generated. In the original algorithm, this was a burst of white noiseWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
, but it can also include any widebandWidebandIn communications, wideband is a relative term used to describe a wide range of frequencies in a spectrum. A system is typically described as wideband if the message bandwidth significantly exceeds the channel's coherence bandwidth....
signal, such as a rapid sine waveSine waveThe sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
chirpChirpA chirp is a signal in which the frequency increases or decreases with time. In some sources, the term chirp is used interchangeably with sweep signal. It is commonly used in sonar and radar, but has other applications, such as in spread spectrum communications...
or frequency sweep, or a single cycle of a sawtooth waveSawtooth waveThe sawtooth wave is a kind of non-sinusoidal waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw....
or square waveSquare waveA square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...
. - This excitation is output and simultaneously fed back into a delay lineDelay lineDelay line may refer to:* Propagation delay, the length of time taken for something to reach its destination* Analog delay line, used to delay a signal...
L samples long. - The output of the delay line is fed through a filterAudio filterAn audio filter is a frequency dependent amplifier circuit, working in the audio frequency range, 0 Hz to beyond 20 kHz. Many types of filters exist for applications including graphic equalizers, synthesizers, sound effects, CD players and virtual reality systems.Being a frequency dependent...
. The gainGainIn electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...
of the filter must be less than 1 at all frequencies, to maintain a stable positive feedback loop. The filter is usually a first-order lowpass filter (as pictured). In the original algorithm, the filter consisted of averaging two adjacent samples, a particularly cheap filter that can be done without a multiplier (just shift and add operations). - The filtered output is simultaneously mixed back into the output and fed back into the delay line.
Tuning the string
The fundamental frequencyFundamental frequency
The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...
(specifically, the lowest nonzero resonant frequency) of the resulting signal is the lowest frequency at which the unwrapped phase response of the delay and filter in cascade is
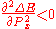. The required phase delay D for a given fundamental frequency F0 is therefore calculated according to D = Fs/F0 where Fs is the sampling frequency.The length of any digital delay line is a whole-number multiple of the sampling period. In order to obtain a fractional delay, interpolating filters
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
are used with parameters selected to obtain an appropriate phase delay at the fundamental frequency. Either IIR
Infinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
or FIR
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
filters may be used, however FIR have the advantage that transients are suppressed if the fractional delay is changed over time. The most elementary fractional delay is the linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
between two samples (e.g., s(4.2) = 0.8s(4) + 0.2s(5)). If the phase delay varies with frequency, harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
s may be sharpened or flattened relative to the fundamental frequency. The original algorithm used equal weighting on two adjacent samples, as this can be achieved without multiplication hardware, allowing extremely cheap implementations.
Z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
analysis can be used to get the pitches and decay times of the harmonics more precisely, as explained in the 1983 paper that introduced the algorithm.
A demonstration of the Karplus-Strong algorithm can be heard in the following Vorbis
Vorbis
Vorbis is a free software / open source project headed by the Xiph.Org Foundation . The project produces an audio format specification and software implementation for lossy audio compression...
file. The algorithm used a loop gain of 0.98 with increasingly attenuating first order lowpass filters. The pitch of the note was A2, or 220 Hz.
Holding the period (= length of the delay line) constant produces vibrations similar to those of a string or bell. Increasing the period sharply after the transient input produces drum-like sounds.
Refinements to the algorithm
Alex Strong and Kevin KarplusKevin Karplus
Kevin Karplus is a professor at University of California, Santa Cruz, currently in the Biomolecular Engineering Department.He is probably best known for work he did as a computer science graduate student at Stanford University on the Karplus-Strong string synthesis algorithm.He taught VLSI design...
realized that the Karplus-Strong algorithm was physically analogous to a sampling of the transversal wave on a string instrument, with the filter in the feedback loop representing the total string losses over one period. Julius O. Smith III http://ccrma.stanford.edu/~jos/ and others
generalized the algorithm to digital waveguide synthesis
Digital waveguide synthesis
Digital waveguide synthesis is the synthesis of audio using a digital waveguide. Digital waveguides are efficient computational models for physical media through which acoustic waves propagate...
, which could also be used to model acoustic waves in tubes and on drum membranes.
Alex Strong developed a superior wavetable-modification method for plucked-string synthesis, but only published it as a patent.
Musical Applications
The first musical use of the algorithm was in the work May All Your Children Be Acrobats written in 1981 by David A. JaffeDavid A. Jaffe
David Aaron Jaffe is an American composer who has written over ninety works for orchestra, chorus, chamber ensembles, and electronics. He is best known for his use of technology as an electronic-music or computer-music composer in works such as Silicon Valley Breakdown, though his non-electronic...
, and scored for eight guitars, mezzo-soprano and computer-generated stereo tape, with a text based on Carl Sandburg
Carl Sandburg
Carl Sandburg was an American writer and editor, best known for his poetry. He won three Pulitzer Prizes, two for his poetry and another for a biography of Abraham Lincoln. H. L. Mencken called Carl Sandburg "indubitably an American in every pulse-beat."-Biography:Sandburg was born in Galesburg,...
's The People, Yes. Jaffe continued to explore the musical and technical possibilities of the algorithm in Silicon Valley Breakdown, for computer-generated plucked strings (1982), as well as in later works such as Telegram to the President, 1984 for string quartet and tape, and Grass for female chorus and tape (1987).
The patent was licensed first to Mattel Electronics, which failed as a company before any product using the algorithm was developed, then to a startup company founded by some of the laid-off Mattel executives. They never got sufficient funding to finish development, and so never brought a product to market either. Eventually Yamaha licensed the patent, as part of the Sondius package of patents from Stanford. It is unknown whether any hardware using the algorithm was ever sold, though many software implementations (which did not pay any license fees to the inventors) have been released.