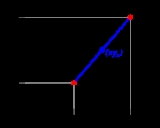
Linear interpolation
Encyclopedia
Linear interpolation is a method of curve fitting
using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .
If the two known points are given by the coordinates 
and 
, the linear interpolant is the straight line between these points. For a value x in the interval 
, the value y along the straight line is given from the equation
which can be derived geometrically from the figure on the right. It is a special case of polynomial interpolation with n = 1.
Solving this equation for y, which is the unknown value at x, gives
which is the formula for linear interpolation in the interval
. Outside this interval, the formula is identical to linear extrapolation.
This formula can also be understood as a weighted average. The weights are inversely related to the distance from the end points to the unknown point; the closer point has more influence than the farther point. Thus, the weights are
and 
, which are normalized distances between the unknown point and each of the end points.
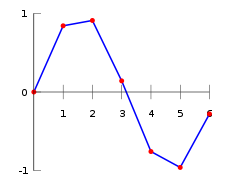Linear interpolation on a set of data points (x0 , y0), (x1 , y1), ..., (xn , yn) is defined as the concatenation of linear interpolants between each pair of data points. This results in a continuous curve
, with a discontinuous derivative (in general), thus of differentiability class
.
f using two known values of that function at other points. The error of this approximation is defined as
where p denotes the linear interpolation polynomial
defined above
It can be proven using Rolle's theorem
that if f has a continuous second derivative, the error is bounded by
As you see, the approximation between two points on a given function gets worse with the second derivative of the function that is approximated. This is intuitively correct as well: the "curvier" the function is, the worse the approximations made with simple linear interpolation.
The basic operation of linear interpolation between two values is so commonly used in computer graphics
that it is sometimes called a lerp in that field's jargon. The term can be used as a verb
or noun
for the operation. e.g. "Bresenham's algorithm lerps incrementally between the two endpoints of the line."
Lerp operations are built into the hardware of all modern computer graphics processors. They are often used as building blocks for more complex operations: for example, a bilinear interpolation
can be accomplished in two lerps. Because this operation is cheap, it's also a good way to implement accurate lookup table
s with quick lookup for smooth function
s without having too many table entries.
, or even polynomial interpolation
in some cases.
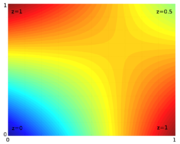
, and in three dimensions, trilinear interpolation
. Notice, though, that these interpolants are no longer linear functions of the spatial coordinates, rather products of linear functions; this is illustrated by the clearly non-linear example of bilinear interpolation
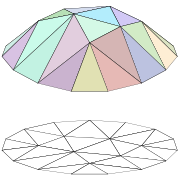
in the figure below. Other extensions of linear interpolation can be applied to other kinds of mesh
such as triangular and tetrahedral meshes, including Bézier surface
s. These may be defined as indeed higher dimensional piecewise linear function (see second figure below).
data. It is believed that it was used by Babylonian astronomers and mathematicians
in Seleucid
Mesopotamia
(last three centuries BC), and by the Greek astronomer
and mathematician
, Hipparchus
(2nd century BC). A description of linear interpolation can be found in the Almagest
(2nd century AD) by Ptolemy
.
Curve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .
Linear interpolation between two known points
and , the linear interpolant is the straight line between these points. For a value x in the interval , the value y along the straight line is given from the equationwhich can be derived geometrically from the figure on the right. It is a special case of polynomial interpolation with n = 1.
Solving this equation for y, which is the unknown value at x, gives
which is the formula for linear interpolation in the interval
. Outside this interval, the formula is identical to linear extrapolation.This formula can also be understood as a weighted average. The weights are inversely related to the distance from the end points to the unknown point; the closer point has more influence than the farther point. Thus, the weights are
and , which are normalized distances between the unknown point and each of the end points.Interpolation of a data set
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, with a discontinuous derivative (in general), thus of differentiability class
.Linear interpolation as approximation
Linear interpolation is often used to approximate a value of some functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f using two known values of that function at other points. The error of this approximation is defined as
where p denotes the linear interpolation polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
defined above
It can be proven using Rolle's theorem
Rolle's theorem
In calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...
that if f has a continuous second derivative, the error is bounded by
As you see, the approximation between two points on a given function gets worse with the second derivative of the function that is approximated. This is intuitively correct as well: the "curvier" the function is, the worse the approximations made with simple linear interpolation.
Applications
Linear interpolation is often used to fill the gaps in a table. Suppose that one has a table listing the population of some country in 1970, 1980, 1990 and 2000, and that one wanted to estimate the population in 1994. Linear interpolation is an easy way to do this.The basic operation of linear interpolation between two values is so commonly used in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
that it is sometimes called a lerp in that field's jargon. The term can be used as a verb
Verb
A verb, from the Latin verbum meaning word, is a word that in syntax conveys an action , or a state of being . In the usual description of English, the basic form, with or without the particle to, is the infinitive...
or noun
Noun
In linguistics, a noun is a member of a large, open lexical category whose members can occur as the main word in the subject of a clause, the object of a verb, or the object of a preposition .Lexical categories are defined in terms of how their members combine with other kinds of...
for the operation. e.g. "Bresenham's algorithm lerps incrementally between the two endpoints of the line."
Lerp operations are built into the hardware of all modern computer graphics processors. They are often used as building blocks for more complex operations: for example, a bilinear interpolation
Bilinear interpolation
In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
can be accomplished in two lerps. Because this operation is cheap, it's also a good way to implement accurate lookup table
Lookup table
In computer science, a lookup table is a data structure, usually an array or associative array, often used to replace a runtime computation with a simpler array indexing operation. The savings in terms of processing time can be significant, since retrieving a value from memory is often faster than...
s with quick lookup for smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s without having too many table entries.
Accuracy
If a C0 function is insufficient, for example if the process that has produced the data points is known be smoother than C0, it is common to replace linear interpolation with spline interpolationSpline interpolation
In the mathematical field of numerical analysis, spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline. Spline interpolation is preferred over polynomial interpolation because the interpolation error can be made small even...
, or even polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
in some cases.
Multivariate
Linear interpolation as described here is for data points in one spatial dimension. For two spatial dimensions, the extension of linear interpolation is called bilinear interpolationBilinear interpolation
In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
, and in three dimensions, trilinear interpolation
Trilinear interpolation
Trilinear interpolation is a method of multivariate interpolation on a 3-dimensional regular grid. It approximates the value of an intermediate point within the local axial rectangular prism linearly, using data on the lattice points...
. Notice, though, that these interpolants are no longer linear functions of the spatial coordinates, rather products of linear functions; this is illustrated by the clearly non-linear example of bilinear interpolation
Bilinear interpolation
In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
in the figure below. Other extensions of linear interpolation can be applied to other kinds of mesh
Polygon mesh
A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...
such as triangular and tetrahedral meshes, including Bézier surface
Bézier surface
Bézier surfaces are a species of mathematical spline used in computer graphics, computer-aided design, and finite element modeling.As with the Bézier curve, a Bézier surface is defined by a set of control points...
s. These may be defined as indeed higher dimensional piecewise linear function (see second figure below).
History
Linear interpolation has been used since antiquity for filling the gaps in tables, often with astronomicalAstronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
data. It is believed that it was used by Babylonian astronomers and mathematicians
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
in Seleucid
Seleucid Empire
The Seleucid Empire was a Greek-Macedonian state that was created out of the eastern conquests of Alexander the Great. At the height of its power, it included central Anatolia, the Levant, Mesopotamia, Persia, today's Turkmenistan, Pamir and parts of Pakistan.The Seleucid Empire was a major centre...
Mesopotamia
Mesopotamia
Mesopotamia is a toponym for the area of the Tigris–Euphrates river system, largely corresponding to modern-day Iraq, northeastern Syria, southeastern Turkey and southwestern Iran.Widely considered to be the cradle of civilization, Bronze Age Mesopotamia included Sumer and the...
(last three centuries BC), and by the Greek astronomer
Greek astronomy
Greek astronomy is astronomy written in the Greek language in classical antiquity. Greek astronomy is understood to include the ancient Greek, Hellenistic, Greco-Roman, and Late Antiquity eras. It is not limited geographically to Greece or to ethnic Greeks, as the Greek language had become the...
and mathematician
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
, Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
(2nd century BC). A description of linear interpolation can be found in the Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
(2nd century AD) by Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
.
See also
- Bilinear interpolationBilinear interpolationIn mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
- Spline interpolationSpline interpolationIn the mathematical field of numerical analysis, spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline. Spline interpolation is preferred over polynomial interpolation because the interpolation error can be made small even...
- Polynomial interpolationPolynomial interpolationIn numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
- de Casteljau's algorithmDe Casteljau's algorithmIn the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau...
- First-order holdFirst-order holdThe first-order hold is a mathematical model of the practical reconstruction of sampled signals that could be done by a conventional digital-to-analog converter and an analog circuit called an integrator. For the FOH, the signal is reconstructed as a piecewise linear approximation to the...
External links
- Equations of the Straight Line at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Implementing linear interpolation in Microsoft Excel