
Bézier surface
Encyclopedia
Bézier surfaces are a species of mathematical spline
used in computer graphics
, computer-aided design
, and finite element modeling.
As with the Bézier curve
, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive, and for many applications, mathematically convenient.
engineer Pierre Bézier
who used them to design automobile
bodies. Bézier surfaces can be of any degree, but bicubic Bézier surfaces generally provide enough degrees of freedom
for most applications.
into a smooth-continuous surface embedded within a space of the same dimensionality as { ki,j }. For example, if k are all points in a four-dimensional space, then the surface will be within a four-dimensional space.
A two-dimensional Bézier surface can be defined as a parametric surface
where the position of a point p as a function of the parametric coordinates u, v is given by:
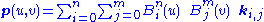
evaluated over the unit square
, where
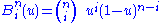
is a Bernstein polynomial
, and
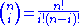
is the binomial coefficient
.
Some properties of Bézier surfaces:
Generally, the most common use of Bézier surfaces is as nets of bicubic patches (where m = n = 3). The geometry of a single bicubic patch is thus completely defined by a set of 16 control points. These are typically linked up to form a B-spline surface in a similar way to the way Bézier curves are linked up to form a B-spline
curve.
Simpler Bézier surfaces are formed from biquadratic patches (m = n = 2), or Bézier triangles.
properties. In addition, other common parametric surfaces such as sphere
s and cylinder
s can be well approximated by relatively small numbers of cubic Bézier patches.
However, Bézier patch meshes are difficult to render directly. One problem with Bézier patches is that calculating their intersections with lines is difficult, making them awkward for pure ray tracing or other direct geometric techniques which do not use subdivision or successive approximation techniques.
They are also difficult to combine directly with perspective projection algorithms.
For this reason, Bézier patch meshes are in general eventually decomposed into meshes of flat triangles by 3D rendering pipelines. In high-quality rendering, the subdivision is adjusted to be so fine that the individual triangle boundaries cannot be seen. To avoid a "blobby" look, fine detail is usually applied to Bézier surfaces at this stage using texture maps, bump maps and other pixel shader techniques.
A Bézier patch of degree (m, n) may be constructed out of two Bézier triangles of degree m+n, or out of a single Bézier triangle of degree m + n, with the input domain as a square
instead of as a triangle
.
A Bézier triangle of degree m may also be constructed out of a Bézier surface of degree (m, m), with the control points so that one edge is squashed to a point, or with the input domain as a triangle instead of as a square.
Spline (mathematics)
In mathematics, a spline is a sufficiently smooth piecewise-polynomial function. In interpolating problems, spline interpolation is often preferred to polynomial interpolation because it yields similar results, even when using low-degree polynomials, while avoiding Runge's phenomenon for higher...
used in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, computer-aided design
Computer-aided design
Computer-aided design , also known as computer-aided design and drafting , is the use of computer technology for the process of design and design-documentation. Computer Aided Drafting describes the process of drafting with a computer...
, and finite element modeling.
As with the Bézier curve
Bézier curve
A Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
, a Bézier surface is defined by a set of control points. Similar to interpolation in many respects, a key difference is that the surface does not, in general, pass through the central control points; rather, it is "stretched" toward them as though each were an attractive force. They are visually intuitive, and for many applications, mathematically convenient.
History
Bézier surfaces were first described in 1962 by the FrenchFrance
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
engineer Pierre Bézier
Pierre Bézier
Pierre Étienne Bézier was a French engineer and one of the founders of the fields of solid, geometric and physical modeling as well as in the field of representing curves, especially in CAD/CAM systems...
who used them to design automobile
Automobile
An automobile, autocar, motor car or car is a wheeled motor vehicle used for transporting passengers, which also carries its own engine or motor...
bodies. Bézier surfaces can be of any degree, but bicubic Bézier surfaces generally provide enough degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
for most applications.
Equation
A given Bézier surface of order (n, m) is defined by a set of (n + 1)(m + 1) control points ki,j. It maps the unit squareUnit square
In mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
into a smooth-continuous surface embedded within a space of the same dimensionality as { ki,j }. For example, if k are all points in a four-dimensional space, then the surface will be within a four-dimensional space.
A two-dimensional Bézier surface can be defined as a parametric surface
Parametric surface
A parametric surface is a surface in the Euclidean space R3 which is defined by a parametric equation with two parameters. Parametric representation is the most general way to specify a surface. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence...
where the position of a point p as a function of the parametric coordinates u, v is given by:
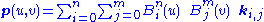
evaluated over the unit square
Unit square
In mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
, where
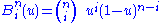
is a Bernstein polynomial
Bernstein polynomial
In the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials....
, and
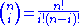
is the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
.
Some properties of Bézier surfaces:
- A Bézier surface will transform in the same way as its control points under all linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s and translationTranslationTranslation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
s. - All u = constant and v = constant lines in the (u, v) space, and, in particular, all four edges of the deformed (u, v) unit square are Bézier curves.
- A Bézier surface will lie completely within the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of its control points, and therefore also completely within the bounding box of its control points in any given Cartesian coordinate systemCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
. - The points in the patch corresponding to the corners of the deformed unit square coincide with four of the control points.
- However, a Bézier surface does not generally pass through its other control points.
Generally, the most common use of Bézier surfaces is as nets of bicubic patches (where m = n = 3). The geometry of a single bicubic patch is thus completely defined by a set of 16 control points. These are typically linked up to form a B-spline surface in a similar way to the way Bézier curves are linked up to form a B-spline
B-spline
In the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...
curve.
Simpler Bézier surfaces are formed from biquadratic patches (m = n = 2), or Bézier triangles.
Bézier surfaces in computer graphics
Bézier patch meshes are superior to meshes of triangles as a representation of smooth surfaces, since they are much more compact, easier to manipulate, and have much better continuityContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
properties. In addition, other common parametric surfaces such as sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s and cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
s can be well approximated by relatively small numbers of cubic Bézier patches.
However, Bézier patch meshes are difficult to render directly. One problem with Bézier patches is that calculating their intersections with lines is difficult, making them awkward for pure ray tracing or other direct geometric techniques which do not use subdivision or successive approximation techniques.
They are also difficult to combine directly with perspective projection algorithms.
For this reason, Bézier patch meshes are in general eventually decomposed into meshes of flat triangles by 3D rendering pipelines. In high-quality rendering, the subdivision is adjusted to be so fine that the individual triangle boundaries cannot be seen. To avoid a "blobby" look, fine detail is usually applied to Bézier surfaces at this stage using texture maps, bump maps and other pixel shader techniques.
A Bézier patch of degree (m, n) may be constructed out of two Bézier triangles of degree m+n, or out of a single Bézier triangle of degree m + n, with the input domain as a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
instead of as a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
.
A Bézier triangle of degree m may also be constructed out of a Bézier surface of degree (m, m), with the control points so that one edge is squashed to a point, or with the input domain as a triangle instead of as a square.
See also
- NURBS
- Computational geometryComputational geometryComputational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
- Bicubic interpolationBicubic interpolationIn mathematics, bicubic interpolation is an extension of cubic interpolation for interpolating data points on a two dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation...
- Bézier curveBézier curveA Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
- Bézier triangle
External links
- http://local.wasp.uwa.edu.au/~pbourke/geometry/bezier/index.html
- http://home.scarlet.be/piet.verplancken3/bezier/node15.html

