
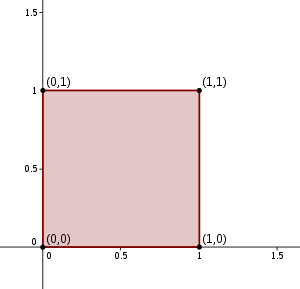
Unit square
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a unit square is a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at (0, 0), (1, 0), (0, 1), and (1, 1).
In the real plane
In a Cartesian coordinate system with coordinates (x , y) the unit square is defined as the squareSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
consisting of the points where both x and y lie in a closed unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
from 0 to 1 on their respective axes.
That is, the unit square is the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
× , where denotes the closed unit interval.
It is not known whether any point in the plane is a rational distance from all four vertices of the unit square. However, no such point is on an edge of the square.
In the complex plane
In the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, the corners of the unit square are at 0, 1,
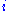 , and 1 +
, and 1 + 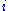 .
.

