Bilinear interpolation
Encyclopedia
In mathematics
, bilinear interpolation is an extension of linear interpolation
for interpolating
functions of two variables (e.g.,
and 
) on a regular grid
. The interpolated function should not use the term of
or 
, but 
, which is the bilinear form of 
and 
.
The key idea is to perform linear interpolation first in one direction, and then again in the other direction. Although each step is linear in the sampled values and in the position, the interpolation as a whole is not linear but rather quadratic in the sample location (details below).
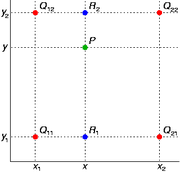
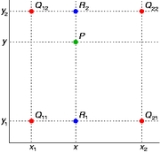
Suppose that we want to find the value of the unknown function f at the point P = (x, y). It is assumed that we know the value of f at the four points Q11 = (x1, y1), Q12 = (x1, y2), Q21 = (x2, y1), and Q22 = (x2, y2).
We first do linear interpolation in the x-direction. This yields
where
,
where
We proceed by interpolating in the y-direction.
This gives us the desired estimate of f(x, y).
Unit Square
If we choose a coordinate system in which the four points where f is known are (0, 0), (0, 1), (1, 0), and (1, 1), then the interpolation formula simplifies to
Or equivalently, in matrix operations:
Nonlinear
Contrary to what the name suggests, the bilinear interpolant is not linear; rather, it is a product of two linear functions:
Alternatively, the interpolant can be written as
where
In both cases, the number of constants (four) correspond to the number of data points where f is given. The interpolant is linear along lines parallel
to either the
or the 
direction, equivalently if 
or 
is set constant. Along any other straight line, the interpolant is quadratic
.
The result of bilinear interpolation is independent of the order (order here meaning which axis is interpolated first and which second) of interpolation. If we had first performed the linear interpolation in the y-direction and then in the x-direction, the resulting approximation would be the same.
The obvious extension of bilinear interpolation to three dimensions is called trilinear interpolation
.
and image processing
, bilinear interpolation is one of the basic resampling
techniques.
In texture mapping
, it is also known as bilinear filtering
or bilinear texture mapping, and it can be used to produce a reasonably realistic image. An algorithm is used to map a screen pixel location to a corresponding point on the texture map. A weighted average of the attributes (color, alpha, etc.) of the four surrounding texels is computed and applied to the screen pixel. This process is repeated for each pixel forming the object being textured.
When an image needs to be scaled up, each pixel of the original image needs to be moved in a certain direction based on the scale constant. However, when scaling up an image by a non-integral scale factor, there are pixels (i.e., holes) that are not assigned appropriate pixel values. In this case, those holes should be assigned appropriate RGB or grayscale
values so that the output image does not have non-valued pixels.
Bilinear interpolation can be used where perfect image transformation with pixel matching is impossible, so that one can calculate and assign appropriate intensity values to pixels. Unlike other interpolation techniques such as nearest neighbor interpolation
and bicubic interpolation
, bilinear interpolation uses only the 4 nearest pixel values which are located in diagonal directions from a given pixel in order to find the appropriate color intensity values of that pixel.
Bilinear interpolation considers the closest 2x2 neighborhood of known pixel values surrounding the unknown pixel's computed location. It then takes a weighted average of these 4 pixels to arrive at its final, interpolated value. The weight on each of the 4 pixel values is based on the computed pixel's distance (in 2D space) from each of the known points.
As seen in this example, the intensity value at the pixel computed to be at row 20.2, column 14.5 can be calculated by first linearly interpolating between the values at column 14 and 15, and then interpolating linearly between rows 20 and 21. Interpolating along the columns produces 150.5 and 128.5 on row 20 and 21. Interpolating between those two values gives
This algorithm reduces some of the visual distortion caused by resizing an image to a non-integral zoom factor, as opposed to nearest neighbor interpolation, which will make some pixels appear larger than others in the resized image. Bilinear interpolation tends, however, to produce a greater number of interpolation artifacts (such as aliasing
, blurring, and edge halos) than more computationally demanding techniques such as bicubic interpolation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, bilinear interpolation is an extension of linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
for interpolating
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
functions of two variables (e.g.,
and ) on a regular gridRegular grid
A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
. The interpolated function should not use the term of
or , but , which is the bilinear form of and .The key idea is to perform linear interpolation first in one direction, and then again in the other direction. Although each step is linear in the sampled values and in the position, the interpolation as a whole is not linear but rather quadratic in the sample location (details below).
We first do linear interpolation in the x-direction. This yields
where
,where
We proceed by interpolating in the y-direction.
This gives us the desired estimate of f(x, y).
Unit Square
If we choose a coordinate system in which the four points where f is known are (0, 0), (0, 1), (1, 0), and (1, 1), then the interpolation formula simplifies to
Or equivalently, in matrix operations:
Nonlinear
Contrary to what the name suggests, the bilinear interpolant is not linear; rather, it is a product of two linear functions:
Alternatively, the interpolant can be written as
where
In both cases, the number of constants (four) correspond to the number of data points where f is given. The interpolant is linear along lines parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to either the
or the direction, equivalently if or is set constant. Along any other straight line, the interpolant is quadraticQuadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
.
The result of bilinear interpolation is independent of the order (order here meaning which axis is interpolated first and which second) of interpolation. If we had first performed the linear interpolation in the y-direction and then in the x-direction, the resulting approximation would be the same.
The obvious extension of bilinear interpolation to three dimensions is called trilinear interpolation
Trilinear interpolation
Trilinear interpolation is a method of multivariate interpolation on a 3-dimensional regular grid. It approximates the value of an intermediate point within the local axial rectangular prism linearly, using data on the lattice points...
.
Application in image processing
In computer visionComputer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
and image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, bilinear interpolation is one of the basic resampling
Resampling
Resampling may refer to:* Resampling , several related audio processes* Resampling , resampling methods in statistics* Resampling , scaling of bitmap images* Sample rate conversion-See also:* Downsampling* Upsampling...
techniques.
In texture mapping
Texture mapping
Texture mapping is a method for adding detail, surface texture , or color to a computer-generated graphic or 3D model. Its application to 3D graphics was pioneered by Dr Edwin Catmull in his Ph.D. thesis of 1974.-Texture mapping:...
, it is also known as bilinear filtering
Bilinear filtering
Bilinear filtering is a texture filtering method used to smooth textures when displayed larger or smaller than they actually are.Most of the time, when drawing a textured shape on the screen, the texture is not displayed exactly as it is stored, without any distortion...
or bilinear texture mapping, and it can be used to produce a reasonably realistic image. An algorithm is used to map a screen pixel location to a corresponding point on the texture map. A weighted average of the attributes (color, alpha, etc.) of the four surrounding texels is computed and applied to the screen pixel. This process is repeated for each pixel forming the object being textured.
When an image needs to be scaled up, each pixel of the original image needs to be moved in a certain direction based on the scale constant. However, when scaling up an image by a non-integral scale factor, there are pixels (i.e., holes) that are not assigned appropriate pixel values. In this case, those holes should be assigned appropriate RGB or grayscale
Grayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
values so that the output image does not have non-valued pixels.
Bilinear interpolation can be used where perfect image transformation with pixel matching is impossible, so that one can calculate and assign appropriate intensity values to pixels. Unlike other interpolation techniques such as nearest neighbor interpolation
Nearest neighbor interpolation
Nearest-neighbor interpolation is a simple method of multivariate interpolation in one or more dimensions....
and bicubic interpolation
Bicubic interpolation
In mathematics, bicubic interpolation is an extension of cubic interpolation for interpolating data points on a two dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation...
, bilinear interpolation uses only the 4 nearest pixel values which are located in diagonal directions from a given pixel in order to find the appropriate color intensity values of that pixel.
Bilinear interpolation considers the closest 2x2 neighborhood of known pixel values surrounding the unknown pixel's computed location. It then takes a weighted average of these 4 pixels to arrive at its final, interpolated value. The weight on each of the 4 pixel values is based on the computed pixel's distance (in 2D space) from each of the known points.
As seen in this example, the intensity value at the pixel computed to be at row 20.2, column 14.5 can be calculated by first linearly interpolating between the values at column 14 and 15, and then interpolating linearly between rows 20 and 21. Interpolating along the columns produces 150.5 and 128.5 on row 20 and 21. Interpolating between those two values gives
This algorithm reduces some of the visual distortion caused by resizing an image to a non-integral zoom factor, as opposed to nearest neighbor interpolation, which will make some pixels appear larger than others in the resized image. Bilinear interpolation tends, however, to produce a greater number of interpolation artifacts (such as aliasing
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
, blurring, and edge halos) than more computationally demanding techniques such as bicubic interpolation.
See also
- Bicubic interpolationBicubic interpolationIn mathematics, bicubic interpolation is an extension of cubic interpolation for interpolating data points on a two dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation...
- Trilinear interpolationTrilinear interpolationTrilinear interpolation is a method of multivariate interpolation on a 3-dimensional regular grid. It approximates the value of an intermediate point within the local axial rectangular prism linearly, using data on the lattice points...
- Spline interpolationSpline interpolationIn the mathematical field of numerical analysis, spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline. Spline interpolation is preferred over polynomial interpolation because the interpolation error can be made small even...
- Lanczos resamplingLanczos resamplingLanczos resampling is an interpolation method used to compute new values for sampled data. It is often used in multivariate interpolation, for example for image scaling , but can be used for any other digital signal...
- Stairstep interpolationStairstep interpolationIn image processing, stairstep interpolation is a general method for interpolating the pixels after enlarging an image. The key idea is to interpolate multiple times in small increments using any interpolation algorithm that is better than nearest-neighbor interpolation, such as bilinear...