Trilinear interpolation
Encyclopedia
Trilinear interpolation is a method of multivariate interpolation
on a 3-dimensional regular grid
. It approximates the value of an intermediate point
within the local axial rectangular prism
linearly, using data on the lattice points. For an arbitrary, unstructured mesh
(as used in finite element analysis), other methods of interpolation must be used; if all the mesh elements are tetrahedra
(3D simplices
), then barycentric coordinates provide a straightforward procedure.
Trilinear interpolation is frequently used in numerical analysis
, data analysis
, and computer graphics
.
, which operates in spaces with dimension
, and bilinear interpolation
, which operates with dimension
, to dimension 
. The order of accuracy is 1 for all these interpolation schemes, and it requires 
adjacent pre-defined values surrounding the interpolation point. There are several ways to arrive at trilinear interpolation, it is equivalent to 3-dimensional tensor
B-spline
interpolation of order 1, and the trilinear interpolation operator is also a tensor product of 3 linear interpolation operators
, 
, and 
be the differences between each of
, 
, 
and the smaller coordinate related, that is:
Where
indicates the lattice point below 
, and 
indicates the lattice point above 
.
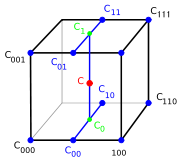First we interpolate along 
(imagine we are pushing the front face of the cube to the back), giving:
Then we interpolate these values (along
, as we were pushing the top edge to the bottom), giving:
Finally we interpolate these values along
(walking through a line):
This gives us a predicted value for the point.
The result of trilinear interpolation is independent of the order of the interpolation steps along the three axes: any other order, for instance along
, then along 
, and finally along 
, produces the same value.
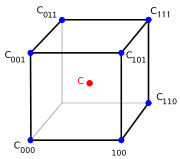
The above operations can be visualized as follows: First we find the eight corners of a cube that surround our point of interest. These corners have the values C000, C100, C010, C110, C001, C101, C011, C111.
Next, we perform linear interpolation between C000 and C100 to find C00, C001 and C101 to find C01, C011 and C111 to find C11, C010 and C110 to find C10.
Now we do interpolation between C00 and C10 to find C0, C01 and C11 to find C1. Finally, we calculate the value C via linear interpolation of C0 and C1
In practice, a trilinear interpolation is identical to three successive linear interpolation
s, or two bilinear interpolation
s combined with a linear interpolation:
Multivariate interpolation
In numerical analysis, multivariate interpolation or spatial interpolation is interpolation on functions of more than one variable.The function to be interpolated is known at given points and the interpolation problem consist of yielding values at arbitrary points .-Regular grid:For function...
on a 3-dimensional regular grid
Regular grid
A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
. It approximates the value of an intermediate point
within the local axial rectangular prismPrism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
linearly, using data on the lattice points. For an arbitrary, unstructured mesh
Unstructured grid
An unstructured grid is a tessellation of a part of the Euclidean plane or Euclidean space by simple shapes, such as triangles or tetrahedra, in an irregular pattern...
(as used in finite element analysis), other methods of interpolation must be used; if all the mesh elements are tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
(3D simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
), then barycentric coordinates provide a straightforward procedure.
Trilinear interpolation is frequently used in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, data analysis
Data analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
, and computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
.
Compared to linear and bilinear interpolation
Trilinear interpolation is the extension of linear interpolationLinear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
, which operates in spaces with dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, and bilinear interpolationBilinear interpolation
In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
, which operates with dimension
, to dimension . The order of accuracy is 1 for all these interpolation schemes, and it requires adjacent pre-defined values surrounding the interpolation point. There are several ways to arrive at trilinear interpolation, it is equivalent to 3-dimensional tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
B-spline
B-spline
In the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...
interpolation of order 1, and the trilinear interpolation operator is also a tensor product of 3 linear interpolation operators
Method
On a periodic and cubic lattice with spacing 1, let, , and be the differences between each of
, , and the smaller coordinate related, that is:Where
indicates the lattice point below , and indicates the lattice point above . (imagine we are pushing the front face of the cube to the back), giving:Then we interpolate these values (along
, as we were pushing the top edge to the bottom), giving:Finally we interpolate these values along
(walking through a line):This gives us a predicted value for the point.
The result of trilinear interpolation is independent of the order of the interpolation steps along the three axes: any other order, for instance along
, then along , and finally along , produces the same value.The above operations can be visualized as follows: First we find the eight corners of a cube that surround our point of interest. These corners have the values C000, C100, C010, C110, C001, C101, C011, C111.
Next, we perform linear interpolation between C000 and C100 to find C00, C001 and C101 to find C01, C011 and C111 to find C11, C010 and C110 to find C10.
Now we do interpolation between C00 and C10 to find C0, C01 and C11 to find C1. Finally, we calculate the value C via linear interpolation of C0 and C1
In practice, a trilinear interpolation is identical to three successive linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
s, or two bilinear interpolation
Bilinear interpolation
In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
s combined with a linear interpolation:
See also
- Linear interpolationLinear interpolationLinear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
- Bilinear interpolationBilinear interpolationIn mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
- Tricubic interpolationTricubic interpolationIn the mathematical subfield numerical analysis, tricubic interpolation is a method for obtaining values at arbitrary points in 3D space of a function defined on a regular grid...
- Radial interpolation
- Tetrahedral interpolation
External links
- pseudo-code from NASA, describes an iterative inverse trilinear interpolation (given the vertices and the value of C find Xd, Yd and Zd).
- Paul Bourke, Interpolation methods, 1999. Contains a very clever and simple method to find trilinear interpolation that is based on binary logic and can be extended to any dimension (Tetralinear, Pentalinear, ...).