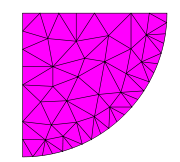
An unstructured grid is a tessellation

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

 of a part of the Euclidean plane or Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 by simple shapes, such as triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

s or tetrahedra

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

, in an irregular pattern. Grids of this type may be used in finite element analysis when the input to be analyzed has an irregular shape.

Unlike structured grids, unstructured grids require a list of the connectivity

Connectivity (graph theory)

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...

 which specifies the way a given set of vertices make up individual elements (see graph (data structure)

Graph (data structure)

In computer science, a graph is an abstract data structure that is meant to implement the graph and hypergraph concepts from mathematics.A graph data structure consists of a finite set of ordered pairs, called edges or arcs, of certain entities called nodes or vertices...

).

Ruppert's algorithm

Ruppert's algorithm

In mesh generation, Ruppert's algorithm, also known as Delaunay refinement, is an algorithm for creating quality Delaunay triangulations. The algorithm takes a planar straight-line graph and returns a conforming Delaunay triangulation of only quality triangles...

is often used to convert an irregularly shaped polygon into an unstructured grid of triangles.

In addition to triangles and tetrahedra, other commonly used elements in finite element simulation include quadrilateral (4-noded) and hexahedral (8-noded) elements in 2D and 3D, respectively. One of the most commonly used algorithms to generate unstructured quadrilateral grid is "Paving". However, there is no such commonly used algorithm for generating unstructured hexahedral grid on a general 3D solid model. "Plastering" is a 3D version of Paving, , but it has difficulty in forming hexahedral elements at the interior of a solid.