Babylonian mathematics - AbsoluteAstronomy.com

Babylonian mathematics refers to any mathematics of the people of Mesopotamia

Mesopotamia

Mesopotamia is a toponym for the area of the Tigris–Euphrates river system, largely corresponding to modern-day Iraq, northeastern Syria, southeastern Turkey and southwestern Iran.Widely considered to be the cradle of civilization, Bronze Age Mesopotamia included Sumer and the...

, from the days of the early Sumer

Sumer

Sumer was a civilization and historical region in southern Mesopotamia, modern Iraq during the Chalcolithic and Early Bronze Age....

ians to the fall of Babylon

Babylon

Babylon was an Akkadian city-state of ancient Mesopotamia, the remains of which are found in present-day Al Hillah, Babil Province, Iraq, about 85 kilometers south of Baghdad...

in 539 BC. Babylonian mathematical texts are plentiful and well edited. In respect of time they fall in two distinct groups: one from the Old Babylonian

First Babylonian Dynasty

The chronology of the first dynasty of Babylonia is debated as there is a Babylonian King List A and a Babylonian King List B. In this chronology, the regnal years of List A are used due to their wide usage...

period (1830-1531 BC), the other mainly Seleucid

Seleucid Empire

The Seleucid Empire was a Greek-Macedonian state that was created out of the eastern conquests of Alexander the Great. At the height of its power, it included central Anatolia, the Levant, Mesopotamia, Persia, today's Turkmenistan, Pamir and parts of Pakistan.The Seleucid Empire was a major centre...

from the last three or four centuries BC. In respect of content there is scarcely any difference between the two groups of texts. Thus Babylonian mathematics remained constant, in character and content, for nearly two millennia. In contrast to the scarcity of sources in Egyptian mathematics

Egyptian mathematics

Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...

, our knowledge of Babylonia

Babylonia

Babylonia was an ancient cultural region in central-southern Mesopotamia , with Babylon as its capital. Babylonia emerged as a major power when Hammurabi Babylonia was an ancient cultural region in central-southern Mesopotamia (present-day Iraq), with Babylon as its capital. Babylonia emerged as...

n mathematics is derived from some 400 clay tablets unearthed since the 1850s. Written in Cuneiform script

Cuneiform script

Cuneiform script )) is one of the earliest known forms of written expression. Emerging in Sumer around the 30th century BC, with predecessors reaching into the late 4th millennium , cuneiform writing began as a system of pictographs...

, tablets were inscribed while the clay was moist, and baked hard in an oven or by the heat of the sun. The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics which include fractions

Fraction (mathematics)

A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...

, algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

, quadratic

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

and cubic equations and the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

. The Babylonian tablet YBC 7289 gives an approximation to

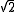accurate to five decimal places.

Babylonian numerals

The Babylonian system of mathematics was sexagesimal (base-60) numeral system

Numeral system

A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....

. From this we derive the modern day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 degrees in a circle. The Babylonians were able to make great advances in mathematics for two reasons. Firstly, the number 60 is a Highly composite number

Highly composite number

A highly composite number is a positive integer with more divisors than any positive integer smaller than itself.The initial or smallest twenty-one highly composite numbers are listed in the table at right....

, having divisors 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60, facilitating calculations with fractions

Fraction (mathematics)

. Additionally, unlike the Egyptians and Romans, the Babylonians and Indians had a true place-value system, where digits written in the left column represented larger values (much as in our base ten system: 734 = 7×100 + 3×10 + 4×1). The Sumerians and Babylonians were pioneers in this respect.

Sumerian mathematics (3000 — 2300 BC)

The ancient Sumer

Sumer

Sumer was a civilization and historical region in southern Mesopotamia, modern Iraq during the Chalcolithic and Early Bronze Age....

ians of Mesopotamia

Mesopotamia

developed a complex system of metrology

Metrology

Metrology is the science of measurement. Metrology includes all theoretical and practical aspects of measurement. The word comes from Greek μέτρον , "measure" + "λόγος" , amongst others meaning "speech, oration, discourse, quote, study, calculation, reason"...

from 3000 BC. From 2600 BC onwards, the Sumerians wrote multiplication table

Multiplication table

In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....

s on clay tablets and dealt with geometrical

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

exercises and division

Division (mathematics)

right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...

problems. The earliest traces of the Babylonian numerals also date back to this period.

Old Babylonian mathematics (2000–1600 BC)

The Old Babylonian

First Babylonian Dynasty

period is the period to which most of the clay tablets on Babylonian mathematics belong, which is why the mathematics of Mesopotamia is commonly known as Babylonian mathematics. Some clay tablets contain mathematical lists and tables, others contain problems and worked solutions.

Arithmetic

The Babylonians made extensive use of pre-calculated tables to assist with arithmetic

Arithmetic

Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...

. For example, two tablets found at Senkerah on the Euphrates

Euphrates

The Euphrates is the longest and one of the most historically important rivers of Western Asia. Together with the Tigris, it is one of the two defining rivers of Mesopotamia...

in 1854, dating from 2000 BC, give lists of the squares

Square number

In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...

of numbers up to 59 and the cubes

Cube (arithmetic)

In arithmetic and algebra, the cube of a number n is its third power — the result of the number multiplying by itself three times:...

of numbers up to 32. The Babylonians used the lists of squares together with the formulas

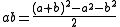
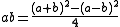
to simplify multiplication.

The Babylonians did not have an algorithm for long division

Long division

In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...

. Instead they based their method on the fact that

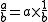
together with a table of reciprocals

Multiplicative inverse

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...

. Numbers whose only prime factor

Prime factor

In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...

s are 2, 3 or 5 (known as 5-smooth or regular numbers) have finite reciprocals in sexagesimal notation, and tables with extensive lists of these reciprocals have been found.

Reciprocals such as 1/7, 1/11, 1/13, etc. do not have finite representations in sexagesimal notation. To compute 1/13 or to divide a number by 13 the Babylonians would use an approximation such as

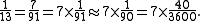
Algebra

As well as arithmetical calculations, Babylonian mathematicians also developed algebraic

Elementary algebra

Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...

methods of solving equation

Equation

An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

s. Once again, these were based on pre-calculated tables.

To solve a quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

, the Babylonians essentially used the standard quadratic formula. They considered quadratic equations of the form

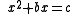
where here b and c were not necessarily integers, but c was always positive. They knew that a solution to this form of equation is

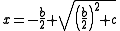
and they would use their tables of squares in reverse to find square roots. They always used the positive root because this made sense when solving "real" problems. Problems of this type included finding the dimensions of a rectangle given its area and the amount by which the length exceeds the width.

Tables of values of n³ + n² were used to solve certain cubic equations. For example, consider the equation

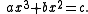
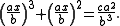
Multiplying the equation by a² and dividing by b³ gives

Substituting y = ax/b gives

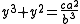
which could now be solved by looking up the n³ + n² table to find the value closest to the right hand side. The Babylonians accomplished this without algebraic notation, showing a remarkable depth of understanding. However, they did not have a method for solving the general cubic equation.

Growth

Babylonians modeled exponential growth, constrained growth (via a form of sigmoid function

Sigmoid function

Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...

s), and doubling time

Doubling time

The doubling time is the period of time required for a quantity to double in size or value. It is applied to population growth, inflation, resource extraction, consumption of goods, compound interest, the volume of malignant tumours, and many other things which tend to grow over time...

, the latter in the context of interest on loans.

Clay tablets from c. 2000 BCE include the exercise "Given an interest rate of 1/60 per month (no compounding), compute the doubling time." This yields an annual interest rate of 12/60 = 20%, and hence a doubling time of 100% growth/20% growth per year = 5 years.

Plimpton 322

The Plimpton 322

Plimpton 322

Plimpton 322 is a Babylonian clay tablet, notable as containing an example of Babylonian mathematics. It has number 322 in the G.A. Plimpton Collection at Columbia University...

tablet contains a list of "Pythagorean triples", i.e., integers

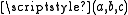such that

.
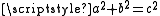The triples are too many and too large to have been obtained by brute force.

Much has been written on the subject, including some speculation (perhaps anachronistic) as to whether the tablet could have served as an early trigonometrical table. Care has to be exercised to see the tablet in terms of methods familiar or
accessible to scribes at the time.

[...] the question “how was the tablet calculated?” does not have to have the
same answer as the question “what problems does the tablet set?” The first can be answered
most satisfactorily by reciprocal pairs, as first suggested half a century ago, and the second
by some sort of right-triangle problems.

(E. Robson, "Neither Sherlock Holmes nor Babylon: a reassessment of Plimpton 322", Historia Math. 28 (3), p. 202).

Geometry

Babylonians knew the common rules for measuring volumes and areas. They measured the circumference of a circle as three times the diameter and the area as one-twelfth the square of the circumference, which would be correct if π is estimated as 3. The volume of a cylinder was taken as the product of the base and the height, however, the volume of the frustum of a cone or a square pyramid was incorrectly taken as the product of the height and half the sum of the bases. The Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

was also known to the Babylonians. Also, there was a recent discovery in which a tablet used π as 3 and 1/8. The Babylonians are also known for the Babylonian mile, which was a measure of distance equal to about seven miles today. This measurement for distances eventually was converted to a time-mile used for measuring the travel of the Sun, therefore, representing time.

The ancient Babylonians had known of theorems on the ratios of the sides of similar triangles for many centuries, but they lacked the concept of an angle measure and consequently, studied the sides of triangles instead.

The Babylonian astronomers kept detailed records on the rising and setting of star

Star

A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...

s, the motion of the planet

Planet

A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...

s, and the solar and lunar eclipse

Eclipse

An eclipse is an astronomical event that occurs when an astronomical object is temporarily obscured, either by passing into the shadow of another body or by having another body pass between it and the viewer...

s, all of which required familiarity with angular

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

distances measured on the celestial sphere

Celestial sphere

In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...

.

They also used a form of Fourier analysis to compute ephemeris

Ephemeris

An ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...

(tables of astronomical positions), which was discovered in the 1950s by Otto Neugebauer.

Influence

Since the rediscovery of the Babylonian civilization, it has become apparent that Greek

Ancient Greece

Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...

and Hellenistic mathematicians and astronomers, and in particular Hipparchus

Hipparchus

Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...

, borrowed greatly from the Babylonia

Babylonia

ns.

Franz Xaver Kugler

Franz Xaver Kugler

Franz Xaver Kugler was a German chemist, mathematician, Assyriologist, and Jesuit priest.Kugler was born in Königsbach, Palatinate, then part of the Kingdom of Bavaria. He earned a Ph.D. in chemistry in 1885, and the following year he entered the Jesuits. By 1893 he had been ordained as a priest...

demonstrated in his book Die Babylonische Mondrechnung ("The Babylonian lunar computation", Freiburg im Breisgau, 1900) the following: Ptolemy had stated in his Almagest IV.2 that Hipparchus improved the values for the Moon's periods known to him from "even more ancient astronomers" by comparing eclipse observations made earlier by "the Chaldeans", and by himself. However Kugler found that the periods that Ptolemy attributes to Hipparchus had already been used in Babylonian ephemerides, specifically the collection of texts nowadays called "System B" (sometimes attributed to Kidinnu

Kidinnu

Kidinnu was a Chaldean astronomer and mathematician. Strabo of Amaseia called him Kidenas, Pliny the Elder Cidenas, and Vettius Valens Kidynas....

). Apparently Hipparchus only confirmed the validity of the periods he learned from the Chaldeans by his newer observations.

It is clear that Hipparchus (and Ptolemy after him) had an essentially complete list of eclipse observations covering many centuries. Most likely these had been compiled from the "diary" tablets: these are clay tablets recording all relevant observations that the Chaldeans routinely made. Preserved examples date from 652 BC to AD 130, but probably the records went back as far as the reign of the Babylonian king Nabonassar

Nabonassar

Nabonassar founded a kingdom in Babylon in 747 BC. This is now considered as the start of the Neo-Babylonian Dynasty. At the time the Assyrian Empire was in disarray through civil war and the ascendancy of other kingdoms such as Urartu...

: Ptolemy starts his chronology with the first day in the Egyptian calendar of the first year of Nabonassar, i.e., 26 February 747 BC.

This raw material by itself must have been hard to use, and no doubt the Chaldeans themselves compiled extracts of e.g., all observed eclipses (some tablets with a list of all eclipses in a period of time covering a saros

Saros cycle

The saros is a period of 223 synodic months , that can be used to predict eclipses of the Sun and Moon. One saros after an eclipse, the Sun, Earth, and Moon return to approximately the same relative geometry, and a nearly identical eclipse will occur, in what is referred to as an eclipse cycle...

have been found). This allowed them to recognise periodic recurrences of events. Among others they used in System B (cf. Almagest IV.2):

223 synodic months = 239 returns in anomaly (anomalistic month) = 242 returns in latitude (draconic month). This is now known as the saros
Saros cycle
The saros is a period of 223 synodic months , that can be used to predict eclipses of the Sun and Moon. One saros after an eclipse, the Sun, Earth, and Moon return to approximately the same relative geometry, and a nearly identical eclipse will occur, in what is referred to as an eclipse cycle...

period which is very useful for predicting eclipse
Eclipse
An eclipse is an astronomical event that occurs when an astronomical object is temporarily obscured, either by passing into the shadow of another body or by having another body pass between it and the viewer...

s.
251 (synodic) months = 269 returns in anomaly
5458 (synodic) months = 5923 returns in latitude
1 synodic month = 29;31:50:08:20 days (sexagesimal; 29.53059413… days in decimals = 29 days 12 hours 44 min 3⅓ s)

The Babylonians expressed all periods in synodic month

Month

A month is a unit of time, used with calendars, which was first used and invented in Mesopotamia, as a natural period related to the motion of the Moon; month and Moon are cognates. The traditional concept arose with the cycle of moon phases; such months are synodic months and last approximately...

s, probably because they used a lunisolar calendar

Lunisolar calendar

A lunisolar calendar is a calendar in many cultures whose date indicates both the moon phase and the time of the solar year. If the solar year is defined as a tropical year then a lunisolar calendar will give an indication of the season; if it is taken as a sidereal year then the calendar will...

. Various relations with yearly phenomena led to different values for the length of the year.

Similarly various relations between the periods of the planet

Planet

s were known. The relations that Ptolemy attributes to Hipparchus in Almagest IX.3 had all already been used in predictions found on Babylonian clay tablets.

All this knowledge was transferred to the Greeks

Greeks

The Greeks, also known as the Hellenes , are a nation and ethnic group native to Greece, Cyprus and neighboring regions. They also form a significant diaspora, with Greek communities established around the world....

probably shortly after the conquest by Alexander the Great (331 BC). According to the late classical philosopher Simplicius

Simplicius of Cilicia

Simplicius of Cilicia, was a disciple of Ammonius Hermiae and Damascius, and was one of the last of the Neoplatonists. He was among the pagan philosophers persecuted by Justinian in the early 6th century, and was forced for a time to seek refuge in the Persian court, before being allowed back into...

(early 6th century AD), Alexander ordered the translation of the historical astronomical records under supervision of his chronicler Callisthenes of Olynthus

Callisthenes

Callisthenes of Olynthus was a Greek historian. He was the son of Hero and Proxenus of Atarneus, which made him the great nephew of Aristotle by his sister Arimneste. They first met when Aristotle tutored Alexander the Great...

, who sent it to his uncle Aristotle

Aristotle

Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...

. It is worth mentioning here that although Simplicius is a very late source, his account may be reliable. He spent some time in exile at the Sassanid (Persian) court, and may have accessed sources otherwise lost in the West. It is striking that he mentions the title tèresis (Greek: guard) which is an odd name for a historical work, but is in fact an adequate translation of the Babylonian title massartu meaning "guarding" but also "observing". Anyway, Aristotle's pupil Callippus of Cyzicus

Callippus

Callippus or Calippus was a Greek astronomer and mathematician.Callippus was born at Cyzicus, and studied under Eudoxus of Cnidus at the Academy of Plato. He also worked with Aristotle at the Lyceum, which means that he was active in Athens prior to Aristotle's death in 322...

introduced his 76-year cycle, which improved upon the 19-year Metonic cycle

Metonic cycle

In astronomy and calendar studies, the Metonic cycle or Enneadecaeteris is a period of very close to 19 years which is remarkable for being very nearly a common multiple of the solar year and the synodic month...

, about that time. He had the first year of his first cycle start at the summer solstice of 28 June 330 BC (Proleptic Julian calendar

Proleptic Julian calendar

The proleptic Julian calendar is produced by extending the Julian calendar to dates preceding AD 4 when its quadrennial leap year stabilized. The leap years actually observed between its official implementation in 45 BC and AD 4 were erratic, see the Julian calendar article for details.A calendar...

date), but later he seems to have counted lunar months from the first month after Alexander's decisive battle at Gaugamela in fall 331 BC. So Callippus may have obtained his data from Babylonian sources and his calendar may have been anticipated by Kidinnu. Also it is known that the Babylonian priest known as Berossus

Berossus

Berossus was a Hellenistic-era Babylonian writer, a priest of Bel Marduk and astronomer writing in Greek, who was active at the beginning of the 3rd century BC...

wrote around 281 BC a book in Greek on the (rather mythological) history of Babylonia, the Babyloniaca, for the new ruler Antiochus I; it is said that later he founded a school of astrology

Astrology

Astrology consists of a number of belief systems which hold that there is a relationship between astronomical phenomena and events in the human world...

on the Greek island of Kos

Kos

Kos or Cos is a Greek island in the south Sporades group of the Dodecanese, next to the Gulf of Gökova/Cos. It measures by , and is from the coast of Bodrum, Turkey and the ancient region of Caria. Administratively the island forms a separate municipality within the Kos peripheral unit, which is...

. Another candidate for teaching the Greeks about Babylonian astronomy

Astronomy

Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...

/astrology

Astrology

Astrology consists of a number of belief systems which hold that there is a relationship between astronomical phenomena and events in the human world...

was Sudines

Sudines

Sudines : Babylonian sage. He is mentioned as one of the famous Chaldean mathematicians and astronomer-astrologers by later Roman writers like Strabo ....

who was at the court of Attalus I Soter

Attalus I

Attalus I , surnamed Soter ruled Pergamon, an Ionian Greek polis , first as dynast, later as king, from 241 BC to 197 BC. He was the second cousin and the adoptive son of Eumenes I, whom he succeeded, and was the first of the Attalid dynasty to assume the title of king in 238 BC...

late in the 3rd century BC.

In any case, the translation of the astronomical records required profound knowledge of the cuneiform script

Cuneiform script

, the language, and the procedures, so it seems likely that it was done by some unidentified Chaldeans. Now, the Babylonians dated their observations in their lunisolar calendar, in which months and years have varying lengths (29 or 30 days; 12 or 13 months respectively). At the time they did not use a regular calendar (such as based on the Metonic cycle

Metonic cycle

like they did later), but started a new month based on observations of the New Moon

New moon

In astronomical terminology, the new moon is the lunar phase that occurs when the Moon, in its monthly orbital motion around Earth, lies between Earth and the Sun, and is therefore in conjunction with the Sun as seen from Earth...

. This made it very tedious to compute the time interval between events.

What Hipparchus may have done is transform these records to the Egyptian calendar

Egyptian calendar

The ancient civil Egyptian calendar had a year that was 360 days long and was divided into 12 months of 30 days each, plus five extra days at the end of the year. The months were divided into three weeks of ten days each...

, which uses a fixed year of always 365 days (consisting of 12 months of 30 days and 5 extra days): this makes computing time intervals much easier. Ptolemy dated all observations in this calendar. He also writes that "All that he (=Hipparchus) did was to make a compilation of the planetary observations arranged in a more useful way" (Almagest IX.2). Pliny states (Naturalis Historia II.IX(53)) on eclipse predictions: "After their time (=Thales

Thales

Thales of Miletus was a pre-Socratic Greek philosopher from Miletus in Asia Minor, and one of the Seven Sages of Greece. Many, most notably Aristotle, regard him as the first philosopher in the Greek tradition...

) the courses of both stars (=Sun and Moon) for 600 years were prophesied by Hipparchus, …". This seems to imply that Hipparchus predicted eclipses for a period of 600 years, but considering the enormous amount of computation required, this is very unlikely. Rather, Hipparchus would have made a list of all eclipses from Nabonasser's time to his own.

Other traces of Babylonian practice in Hipparchus' work are:

first known Greek use of the division the circle in 360 degrees
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...

of 60 arc minutes.
first consistent use of the sexagesimal number system.
the use of the unit pechus ("cubit") of about 2° or 2½°.
use of a short period of 248 days = 9 anomalistic months.

Babylonian numerals

Sumerian mathematics (3000 — 2300 BC)

Old Babylonian mathematics (2000–1600 BC)

Arithmetic

Algebra

Growth

Plimpton 322

Geometry

Influence

See also