Linear filter
Encyclopedia
Linear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.
This results from systems composed solely of components (or digital algorithms) classified as having a linear
response.
Most filters implemented in analog electronics, in digital signal processing
, or in mechanical systems are classified as causal, time invariant, and linear
.
However the general concept of linear filtering is broader, also used in statistics
, data analysis
, and mechanical engineering
among other fields and technologies. This includes noncausal filters and filters in more than one dimension such as would be used in image processing; those filters are subject to different constraints leading to different design methods, which are discussed elsewhere.
A linear time-invariant (LTI
) filter can be uniquely specified by its impulse response
h, and the output of any filter is mathematically expressed as the convolution
of the input with that impulse response. The frequency response
, given by the filter's transfer function
, is an alternative characterization of the filter.
The frequency response may be tailored to, for instance, eliminate unwanted frequency components from an input signal, or to limit an amplifier to signals within a particular band of frequencies. There are a number of particularly desirable or useful filter transfer functions, of which this article will present an overview.
Among the time-domain filters we here consider, there are two general classes of filter transfer functions that can approximate a desired frequency response.
Very different mathematical treatments apply to the design of filters termed infinite impulse response
(IIR) filters, characteristic of mechanical and analog electronics systems, and finite impulse response
(FIR) filters, which can be implemented by discrete time
systems such as computers (then termed digital signal processing
).
h of a linear time-invariant causal filter specifies the output that the filter would produce if it were to receive an input consisting of a single impulse at time 0. An "impulse" in a continuous time filter means a Dirac delta function
; in a discrete time filter the Kronecker delta function would apply. The impulse response completely characterizes the response of any such filter, inasmuch as any possible input signal can be expressed as a (possibly infinite) combination of weighted delta functions. Multiplying the impulse response shifted in time according to the arrival of each of these delta functions by the amplitude of each delta function, and summing these responses together (according to the superposition principle
, applicable to all linear systems) yields the output waveform.
Mathematically this is described as the convolution
of a time-varying input signal x(t) with the filter's impulse response
h, defined as:
The first form is the continuous-time form which describes mechanical and analog electronic systems, for instance. The second equation is a discrete-time version used, for example, by digital filters implemented in software, so-called digital signal processing
. The impluse response h completely characterizes any linear time-invariant (or shift-invariant in the discrete-time case) filter. The input x is said to be "convolved" with the impulse response h having a (possibly infinite) duration of time T (or of N sampling periods).
The filter response can also be completely characterized in the frequency domain by its transfer function
, which is the Fourier transform
of the impulse response h. Typical filter design goals are to realize a particular frequency response, that is, the magnitude of the transfer function
; the importance of the phase of the transfer function varies according to the application, inasmuch as the shape of a waveform can be distorted to a greater or lesser extent in the process of achieving a desired (amplitude) response in the frequency domain.
Filter design consists of finding a possible transfer function that can be implemented within certain practical constraints dictated by the technology or desired complexity of the system, followed by a practical design that realizes that transfer function using the chosen technology. The complexity of a filter may be specified according to the order
of the filter, which is specified differently depending on whether we are dealing with an IIR or FIR filter. We will now look at these two cases.
s and amplifiers). When such a system is subject to an impulse (or any signal of finite duration) it will respond with an output waveform which lasts past the duration of the input, eventually decaying exponentially in one or another manner, but never completely settling to zero (mathematically speaking). Such a system is said to have an infinite impulse response
(IIR). The convolution integral (or summation) above extends over all time: T (or N) must be set to infinity.
For instance, consider a damped harmonic oscillator such as a pendulum, or a resonant L-C tank circuit. If the pendulum has been at rest and we were to strike it with a hammer (the "impulse"), setting it in motion, it would swing back and forth ("resonate"), say, with an amplitude of 10cm. But after 10 minutes, say, it would still be swinging but the amplitude would have decreased to 5 cm, half of its original amplitude. After another 10 minutes its amplitude would be only 2.5 cm, then 1.25 cm, etc. However it would never come to a complete rest, and we therefore call that response to the impulse (striking it with a hammer) "infinite" in duration.
The complexity of such a system is specified by its order
N. N is often a constraint on the design of a transfer function since it specifies the number of reactive components in an analog circuit; in a digital IIR filter the number of computations required is proportional to N.
) is a discrete-time system; a different (but parallel) set of mathematical concepts defines the behavior of such systems. Although a digital filter
can be an IIR filter if the algorithm implementing it includes feedback
, it is also possible to easily implement a filter whose impulse truly goes to zero after N time steps; this is called a finite impulse response
(FIR) filter.
For instance, suppose we have a filter which, when presented with an impulse in a time series:
will output a series which responds to that impulse at time 0 until time 4, and has no further response, such as:
Although the impulse response has lasted 4 time steps after the input, starting at time 5 it has truly gone to zero. The extent of the impulse response is finite, and this would be classified as a 4th order FIR filter.
The convolution integral (or summation) above need only extend to the full duration of the impulse response T, or the order N in a discrete time filter.
A digital IIR filter can generally approximate a desired filter response using less computing power than a FIR filter, however this advantage is more often unneeded given the increasing power of digital processors. The ease of designing and characterizing FIR filters makes them preferable to the filter designer (programmer) when ample computing power is available. Another advantage of FIR filters is that their impulse response can be made symmetric, which implies a response in the frequency domain which has zero phase
at all frequencies (not considering a finite delay), which is absolutely impossible with any IIR filter.
of a filter can be obtained if the impulse response is known, or directly through analysis using Laplace transforms, or in discrete-time systems the Z-transform
. The frequency response also includes the phase
as a function of frequency, however in many cases the phase response is of little or no interest. FIR filters can be made to have zero phase, but with IIR filters that is generally impossible With most IIR transfer functions there are related transfer functions having a frequency response with the same magnitude but a different phase; in most case the so-called minimum phase
transfer function is preferred.
Filters in the time domain are most often requested to follow a specified frequency response. Then a mathematical procedure is used to find a filter transfer function which can be realized (within some constraints) and which approximates the desired response to within some criterion. Common filter response specifications are described as follows:
and fourier transformed to the time domain. This will obtain the filter coefficients hi which will implement a zero phase FIR filter which matches the frequency response at the sampled frequencies used. In order to better match a desired response, 
must be reduced. However the duration of the filter's impulse response, and the number of terms which must be summed for each output value (according to the above discrete time convolution) is given by 
where T is the sampling period of the discrete time system (N-1 is also termed the order of an FIR filter). Thus the complexity of a digital filter and the computing time involved, grows inversely with 
, placing a higher cost on filter functions which better approximate the desired behavior. For the same reason, filter functions whose critical response is at lower frequencies (compared to the sampling frequency 1/T) require a higher order, more computationally intensive FIR filter. An IIR filter can thus be much more efficient in such cases.
Elsewhere the reader may find further discussion of design methods for practical FIR filter design.
s it is possible to convert these continuous time frequency responses to ones that are implemented in discrete time, for use in digital IIR filters. The complexity of any such filter is given by the order N, which describes the order of the rational function
describing the frequency response. The order N is of particular importance in analog filters, because an Nth order electronic filter requires N reactive elements (capactors and/or inductors) to implement. If a filter is implemented using, for instance, biquad stages
using op-amps, N/2 stages will be needed. In a digital implementation, the number of computations performed per sample is proportional to N. Thus the mathematical problem is to obtain the best approximation (in some sense) to the desired response using a smaller N, as we shall now illustrate.
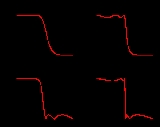
Below are the frequency responses of several standard filter functions which approximate a desired response, optimized according to some criterion. These are all fifth-order low-pass filters, designed for a cutoff frequency of .5 in normalized units. Frequency responses are shown for the Butterworth
, Chebyshev
, inverse Chebyshev, and elliptic filter
s.
As is clear from the image, the elliptic filter is sharper than the others, but at the expense of ripples in both its passband and stopband. The Butterworth filter has the poorest transition but has a more even response, avoiding ripples in either the passband or stopband. A Bessel filter
(not shown) has an even poorer transition in the frequency domain, but maintains the best phase fidelity of a waveform. Different applications will emphasize different design requirements, leading to different choices among these (and other) optimizations, or requiring a filter of a higher order.
design, whose schematic diagram is shown here. This topology can be adapted to produce low-pass, band-pass, and high pass filters.
An Nth order FIR filter can be implemented in a discrete time system using a computer program or specialized hardware in which the input signal is subject to N delay stages. The output of the filter is formed as the weighted sum of those delayed signals, as is depicted in the accompanying signal flow diagram. The response of the filter depends on the weighting coefficients denoted b0, b1, .... bN. For instance, if all of the coefficients were equal to unity, a so-called boxcar function
, then it would implement a low-pass filter with a low frequency gain of N+1 and a frequency response given by the sinc function. Superior shapes for the frequency response can be obtained using coefficients derived from a more sophisticated design procedure.
describes linear time-invariant (LTI) filters of all types. LTI filters can be completely described by their frequency response
and phase response
, the specification of which uniquely defines their impulse response
, and vice versa. From a mathematical viewpoint, continuous-time IIR LTI filters may be described in terms of linear differential equation
s, and their impulse responses considered as Green's function
s of the equation. Continuous-time LTI filters may also be described in terms of the Laplace transform of their impulse response, which allows all of the characteristics of the filter to be analyzed by considering the pattern of poles and zero
s of their Laplace transform in the complex plane
. Similarly, discrete-time LTI filters may be analyzed via the Z-transform
of their impulse response.
Before the advent of computer filter synthesis tools, graphical tools such as Bode plot
s and Nyquist plot
s were extensively used as design tools. Even today, they are invaluable tools to understanding filter behavior. Reference books had extensive plots of frequency response, phase response, group delay, and impulse response for various types of filters, of various orders. They also contained tables of values showing how to implement such filters as RLC ladders - very useful when amplifying elements were expensive compared to passive components. Such a ladder can also be designed to have minimal sensitivity to component variation a property hard to evaluate without computer tools.
Many different analog filter designs have been developed, each trying to optimise some feature of the system response. For practical filters, a custom design is sometimes desirable, that can offer the best tradeoff between different design criteria, which may include component count and cost, as well as filter response characteristics.
These descriptions refer to the mathematical properties of the filter (that is, the frequency and phase response). These can be implemented as analog circuits (for instance, using a Sallen Key filter
topology, a type of active filter
), or as algorithms in digital signal processing
systems.
Digital filters are much more flexible to synthesize and use than analog filters, where the constraints of the design permits their use. Notably, there is no need to consider component tolerances, and very high Q levels may be obtained.
FIR digital filters may be implemented by the direct convolution
of the desired impulse response with the input signal.
They can easily be designed to give a matched filter
for any arbitrary pulse shape.
IIR digital filters are often more difficult to design, due to problems including dynamic range issues, quantization noise and instability.
Typically digital IIR filters are designed as a series of digital biquad filters.
All low-pass second-order continuous-time filters have a transfer function
given by
All band-pass second-order continuous-time have a transfer function given by
where
This results from systems composed solely of components (or digital algorithms) classified as having a linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
response.
Most filters implemented in analog electronics, in digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
, or in mechanical systems are classified as causal, time invariant, and linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
.
However the general concept of linear filtering is broader, also used in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, data analysis
Data analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
, and mechanical engineering
Mechanical engineering
Mechanical engineering is a discipline of engineering that applies the principles of physics and materials science for analysis, design, manufacturing, and maintenance of mechanical systems. It is the branch of engineering that involves the production and usage of heat and mechanical power for the...
among other fields and technologies. This includes noncausal filters and filters in more than one dimension such as would be used in image processing; those filters are subject to different constraints leading to different design methods, which are discussed elsewhere.
A linear time-invariant (LTI
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
) filter can be uniquely specified by its impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
h, and the output of any filter is mathematically expressed as the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of the input with that impulse response. The frequency response
Frequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
, given by the filter's transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
, is an alternative characterization of the filter.The frequency response may be tailored to, for instance, eliminate unwanted frequency components from an input signal, or to limit an amplifier to signals within a particular band of frequencies. There are a number of particularly desirable or useful filter transfer functions, of which this article will present an overview.
Among the time-domain filters we here consider, there are two general classes of filter transfer functions that can approximate a desired frequency response.
Very different mathematical treatments apply to the design of filters termed infinite impulse response
Infinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
(IIR) filters, characteristic of mechanical and analog electronics systems, and finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
(FIR) filters, which can be implemented by discrete time
Discrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
systems such as computers (then termed digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
).
Impulse response and transfer function
The impulse responseImpulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
h of a linear time-invariant causal filter specifies the output that the filter would produce if it were to receive an input consisting of a single impulse at time 0. An "impulse" in a continuous time filter means a Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
; in a discrete time filter the Kronecker delta function would apply. The impulse response completely characterizes the response of any such filter, inasmuch as any possible input signal can be expressed as a (possibly infinite) combination of weighted delta functions. Multiplying the impulse response shifted in time according to the arrival of each of these delta functions by the amplitude of each delta function, and summing these responses together (according to the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
, applicable to all linear systems) yields the output waveform.
Mathematically this is described as the convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of a time-varying input signal x(t) with the filter's impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
h, defined as:
The first form is the continuous-time form which describes mechanical and analog electronic systems, for instance. The second equation is a discrete-time version used, for example, by digital filters implemented in software, so-called digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
. The impluse response h completely characterizes any linear time-invariant (or shift-invariant in the discrete-time case) filter. The input x is said to be "convolved" with the impulse response h having a (possibly infinite) duration of time T (or of N sampling periods).
The filter response can also be completely characterized in the frequency domain by its transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
, which is the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the impulse response h. Typical filter design goals are to realize a particular frequency response, that is, the magnitude of the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
; the importance of the phase of the transfer function varies according to the application, inasmuch as the shape of a waveform can be distorted to a greater or lesser extent in the process of achieving a desired (amplitude) response in the frequency domain.Filter design consists of finding a possible transfer function that can be implemented within certain practical constraints dictated by the technology or desired complexity of the system, followed by a practical design that realizes that transfer function using the chosen technology. The complexity of a filter may be specified according to the order
Order
-Ordinality:*Collation, the sequencing and ordering of text**Alphabetical order**Lexicographical order*Order of precedence-Philosophy:* Natural order * Implicate and explicate order according to David Bohm-Science and mathematics:...
of the filter, which is specified differently depending on whether we are dealing with an IIR or FIR filter. We will now look at these two cases.
Infinite impulse response filters
Consider a physical system that acts as a linear filter, such as a system of springs and masses, or an analog electronic circuit that includes capacitors and/or inductors (along with other linear components such as resistorResistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
s and amplifiers). When such a system is subject to an impulse (or any signal of finite duration) it will respond with an output waveform which lasts past the duration of the input, eventually decaying exponentially in one or another manner, but never completely settling to zero (mathematically speaking). Such a system is said to have an infinite impulse response
Infinite impulse response
Infinite impulse response is a property of signal processing systems. Systems with this property are known as IIR systems or, when dealing with filter systems, as IIR filters. IIR systems have an impulse response function that is non-zero over an infinite length of time...
(IIR). The convolution integral (or summation) above extends over all time: T (or N) must be set to infinity.
For instance, consider a damped harmonic oscillator such as a pendulum, or a resonant L-C tank circuit. If the pendulum has been at rest and we were to strike it with a hammer (the "impulse"), setting it in motion, it would swing back and forth ("resonate"), say, with an amplitude of 10cm. But after 10 minutes, say, it would still be swinging but the amplitude would have decreased to 5 cm, half of its original amplitude. After another 10 minutes its amplitude would be only 2.5 cm, then 1.25 cm, etc. However it would never come to a complete rest, and we therefore call that response to the impulse (striking it with a hammer) "infinite" in duration.
The complexity of such a system is specified by its order
Order
-Ordinality:*Collation, the sequencing and ordering of text**Alphabetical order**Lexicographical order*Order of precedence-Philosophy:* Natural order * Implicate and explicate order according to David Bohm-Science and mathematics:...
N. N is often a constraint on the design of a transfer function since it specifies the number of reactive components in an analog circuit; in a digital IIR filter the number of computations required is proportional to N.
Finite impulse response filters
A filter implemented in a computer program (or a so-called digital signal processorDigital signal processor
A digital signal processor is a specialized microprocessor with an architecture optimized for the fast operational needs of digital signal processing.-Typical characteristics:...
) is a discrete-time system; a different (but parallel) set of mathematical concepts defines the behavior of such systems. Although a digital filter
Digital filter
In electronics, computer science and mathematics, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is...
can be an IIR filter if the algorithm implementing it includes feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
, it is also possible to easily implement a filter whose impulse truly goes to zero after N time steps; this is called a finite impulse response
Finite impulse response
A finite impulse response filter is a type of a signal processing filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response filters, which have internal feedback and may continue to respond indefinitely...
(FIR) filter.
For instance, suppose we have a filter which, when presented with an impulse in a time series:
- 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.....
will output a series which responds to that impulse at time 0 until time 4, and has no further response, such as:
- 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0.....
Although the impulse response has lasted 4 time steps after the input, starting at time 5 it has truly gone to zero. The extent of the impulse response is finite, and this would be classified as a 4th order FIR filter.
The convolution integral (or summation) above need only extend to the full duration of the impulse response T, or the order N in a discrete time filter.
Implementation issues
Classical analog filters are IIR filters, and classical filter theory centers on the determination of transfer functions given by low order rational functions, which can be synthesized using the same small number of reactive components. Using digital computers, on the other hand, both FIR and IIR filters are straightforward to implement in software.A digital IIR filter can generally approximate a desired filter response using less computing power than a FIR filter, however this advantage is more often unneeded given the increasing power of digital processors. The ease of designing and characterizing FIR filters makes them preferable to the filter designer (programmer) when ample computing power is available. Another advantage of FIR filters is that their impulse response can be made symmetric, which implies a response in the frequency domain which has zero phase
Phase
-In physics:*Phase , a physically distinctive form of a substance, such as the solid, liquid, and gaseous states of ordinary matter**Phase transition is the transformation of a thermodynamic system from one phase to another*Phase...
at all frequencies (not considering a finite delay), which is absolutely impossible with any IIR filter.
Frequency response
The frequency response or transfer functionTransfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
of a filter can be obtained if the impulse response is known, or directly through analysis using Laplace transforms, or in discrete-time systems the Z-transformZ-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
. The frequency response also includes the phase
Phase
-In physics:*Phase , a physically distinctive form of a substance, such as the solid, liquid, and gaseous states of ordinary matter**Phase transition is the transformation of a thermodynamic system from one phase to another*Phase...
as a function of frequency, however in many cases the phase response is of little or no interest. FIR filters can be made to have zero phase, but with IIR filters that is generally impossible With most IIR transfer functions there are related transfer functions having a frequency response with the same magnitude but a different phase; in most case the so-called minimum phase
Minimum phase
In control theory and signal processing, a linear, time-invariant system is said to be minimum-phase if the system and its inverse are causal and stable....
transfer function is preferred.
Filters in the time domain are most often requested to follow a specified frequency response. Then a mathematical procedure is used to find a filter transfer function which can be realized (within some constraints) and which approximates the desired response to within some criterion. Common filter response specifications are described as follows:
- A low-pass filterLow-pass filterA low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
passes low frequencies while blocking higher frequencies. - A high-pass filterHigh-pass filterA high-pass filter is a device that passes high frequencies and attenuates frequencies lower than its cutoff frequency. A high-pass filter is usually modeled as a linear time-invariant system...
passes high frequencies. - A band-pass filterBand-pass filterA band-pass filter is a device that passes frequencies within a certain range and rejects frequencies outside that range.Optical band-pass filters are of common usage....
passes a band (range) of frequencies. - A band-stop filterBand-stop filterIn signal processing, a band-stop filter or band-rejection filter is a filter that passes most frequencies unaltered, but attenuates those in a specific range to very low levels. It is the opposite of a band-pass filter...
passes high and low frequencies outside of a specified band. - A notch filter has a null response at a particular frequency. This function may be combined with one of the above responses.
- An all-pass filterAll-pass filterAn all-pass filter is a signal processing filter that passes all frequencies equally, but changes the phase relationship between various frequencies. It does this by varying its propagation delay with frequency...
passes all frequencies equally well, but alters the phase relationship among them. - An equalization filter is not designed to fully pass or block any frequency, but instead to gradually vary the amplitude response as a function of frequency: filters used as pre-emphasis filters, equalizerEqualizationEqualization, is the process of adjusting the balance between frequency components within an electronic signal. The most well known use of equalization is in sound recording and reproduction but there are many other applications in electronics and telecommunications. The circuit or equipment used...
s, or tone controls are good examples.
FIR transfer functions
Meeting a frequency response requirement with an FIR filter uses relatively straight-forward procedures. In the most basic form, the desired frequency response itself can be sampled with a resolution of and fourier transformed to the time domain. This will obtain the filter coefficients hi which will implement a zero phase FIR filter which matches the frequency response at the sampled frequencies used. In order to better match a desired response, must be reduced. However the duration of the filter's impulse response, and the number of terms which must be summed for each output value (according to the above discrete time convolution) is given by where T is the sampling period of the discrete time system (N-1 is also termed the order of an FIR filter). Thus the complexity of a digital filter and the computing time involved, grows inversely with , placing a higher cost on filter functions which better approximate the desired behavior. For the same reason, filter functions whose critical response is at lower frequencies (compared to the sampling frequency 1/T) require a higher order, more computationally intensive FIR filter. An IIR filter can thus be much more efficient in such cases.Elsewhere the reader may find further discussion of design methods for practical FIR filter design.
IIR transfer functions
Since classical analog filters are IIR filters, there has been a long history of studying the range of possible transfer functions implementing various of the above desired filter responses in continuous time systems. Using transformBilinear transform
The bilinear transform is used in digital signal processing and discrete-time control theory to transform continuous-time system representations to discrete-time and vice versa....
s it is possible to convert these continuous time frequency responses to ones that are implemented in discrete time, for use in digital IIR filters. The complexity of any such filter is given by the order N, which describes the order of the rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
describing the frequency response. The order N is of particular importance in analog filters, because an Nth order electronic filter requires N reactive elements (capactors and/or inductors) to implement. If a filter is implemented using, for instance, biquad stages
Active filter
An active filter is a type of analog electronic filter that uses an amplifier stage. Amplifiers included in a filter design can be used to improve the performance, stability and predictability of a filter. An amplifier prevents the impedance of source or load stages from affecting the...
using op-amps, N/2 stages will be needed. In a digital implementation, the number of computations performed per sample is proportional to N. Thus the mathematical problem is to obtain the best approximation (in some sense) to the desired response using a smaller N, as we shall now illustrate.
Below are the frequency responses of several standard filter functions which approximate a desired response, optimized according to some criterion. These are all fifth-order low-pass filters, designed for a cutoff frequency of .5 in normalized units. Frequency responses are shown for the Butterworth
Butterworth filter
The Butterworth filter is a type of signal processing filter designed to have as flat a frequency response as possible in the passband so that it is also termed a maximally flat magnitude filter...
, Chebyshev
Chebyshev filter
Chebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
, inverse Chebyshev, and elliptic filter
Elliptic filter
An elliptic filter is a signal processing filter with equalized ripple behavior in both the passband and the stopband...
s.
Bessel filter
In electronics and signal processing, a Bessel filter is a type of linear filter with a maximally flat group delay . Bessel filters are often used in audio crossover systems...
(not shown) has an even poorer transition in the frequency domain, but maintains the best phase fidelity of a waveform. Different applications will emphasize different design requirements, leading to different choices among these (and other) optimizations, or requiring a filter of a higher order.
Example implementations
A popular circuit implementing a second order active R-C filter is the Sallen-KeySallen Key filter
The Sallen–Key topology is an electronic filter topology used to implement second-order active filters that is particularly valued for its simplicity. It is a degenerate form of a voltage-controlled voltage-source filter topology...
design, whose schematic diagram is shown here. This topology can be adapted to produce low-pass, band-pass, and high pass filters.
An Nth order FIR filter can be implemented in a discrete time system using a computer program or specialized hardware in which the input signal is subject to N delay stages. The output of the filter is formed as the weighted sum of those delayed signals, as is depicted in the accompanying signal flow diagram. The response of the filter depends on the weighting coefficients denoted b0, b1, .... bN. For instance, if all of the coefficients were equal to unity, a so-called boxcar function
Boxcar function
In mathematics, a boxcar function is any function which is zero over the entirereal line except for a single interval where it is equal to a constant, A; it is a simple step function...
, then it would implement a low-pass filter with a low frequency gain of N+1 and a frequency response given by the sinc function. Superior shapes for the frequency response can be obtained using coefficients derived from a more sophisticated design procedure.
Mathematics of filter design
LTI system theoryLTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
describes linear time-invariant (LTI) filters of all types. LTI filters can be completely described by their frequency response
Frequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
and phase response
Phase response
In signal processing and electrical engineering, phase response is the relationship between the phase of a sinusoidal input and the output signal passing through any device that accepts input and produces an output signal, such as an amplifier or a filter....
, the specification of which uniquely defines their impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
, and vice versa. From a mathematical viewpoint, continuous-time IIR LTI filters may be described in terms of linear differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, and their impulse responses considered as Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
s of the equation. Continuous-time LTI filters may also be described in terms of the Laplace transform of their impulse response, which allows all of the characteristics of the filter to be analyzed by considering the pattern of poles and zero
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
s of their Laplace transform in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. Similarly, discrete-time LTI filters may be analyzed via the Z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
of their impulse response.
Before the advent of computer filter synthesis tools, graphical tools such as Bode plot
Bode plot
A Bode plot is a graph of the transfer function of a linear, time-invariant system versus frequency, plotted with a log-frequency axis, to show the system's frequency response...
s and Nyquist plot
Nyquist plot
A Nyquist plot is a parametric plot of a transfer function used in automatic control and signal processing. The most common use of Nyquist plots is for assessing the stability of a system with feedback. In Cartesian coordinates, the real part of the transfer function is plotted on the X axis. The...
s were extensively used as design tools. Even today, they are invaluable tools to understanding filter behavior. Reference books had extensive plots of frequency response, phase response, group delay, and impulse response for various types of filters, of various orders. They also contained tables of values showing how to implement such filters as RLC ladders - very useful when amplifying elements were expensive compared to passive components. Such a ladder can also be designed to have minimal sensitivity to component variation a property hard to evaluate without computer tools.
Many different analog filter designs have been developed, each trying to optimise some feature of the system response. For practical filters, a custom design is sometimes desirable, that can offer the best tradeoff between different design criteria, which may include component count and cost, as well as filter response characteristics.
These descriptions refer to the mathematical properties of the filter (that is, the frequency and phase response). These can be implemented as analog circuits (for instance, using a Sallen Key filter
Sallen Key filter
The Sallen–Key topology is an electronic filter topology used to implement second-order active filters that is particularly valued for its simplicity. It is a degenerate form of a voltage-controlled voltage-source filter topology...
topology, a type of active filter
Active filter
An active filter is a type of analog electronic filter that uses an amplifier stage. Amplifiers included in a filter design can be used to improve the performance, stability and predictability of a filter. An amplifier prevents the impedance of source or load stages from affecting the...
), or as algorithms in digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
systems.
Digital filters are much more flexible to synthesize and use than analog filters, where the constraints of the design permits their use. Notably, there is no need to consider component tolerances, and very high Q levels may be obtained.
FIR digital filters may be implemented by the direct convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of the desired impulse response with the input signal.
They can easily be designed to give a matched filter
Matched filter
In telecommunications, a matched filter is obtained by correlating a known signal, or template, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving the unknown signal with a conjugated time-reversed version of the template...
for any arbitrary pulse shape.
IIR digital filters are often more difficult to design, due to problems including dynamic range issues, quantization noise and instability.
Typically digital IIR filters are designed as a series of digital biquad filters.
All low-pass second-order continuous-time filters have a transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
given by
All band-pass second-order continuous-time have a transfer function given by
where
- K is the gain (low-pass DC gain, or band-pass mid-band gain) (K is 1 for passive filters)
- Q is the Q factorQ factorIn physics and engineering the quality factor or Q factor is a dimensionless parameter that describes how under-damped an oscillator or resonator is, or equivalently, characterizes a resonator's bandwidth relative to its center frequency....
-
is the center frequency -
is the complex frequency
See also
- Filter designFilter designFilter design is the process of designing a filter , often a linear shift-invariant filter, that satisfies a set of requirements, some of which are contradictory...
- Laplace transform
- Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
- Prototype filterPrototype filterPrototype filters are electronic filter designs that are used as a template to produce a modified filter design for a particular application. They are an example of a nondimensionalised design from which the desired filter can be scaled or transformed. They are most often seen in regards to...
- Z-transformZ-transformIn mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
- System theory
- LTI system theoryLTI system theoryLinear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
- LTI system theory
- Nonlinear filter
- Wiener filterWiener filterIn signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
- Gabor filterGabor filterIn image processing, a Gabor filter, named after Dennis Gabor, is a linear filter used for edge detection. Frequency and orientation representations of Gabor filters are similar to those of the human visual system, and they have been found to be particularly appropriate for texture representation...
Further reading
- National Semiconductor AN-779 application note describing analog filter theory
- Lattice AN6017 application note comparing and contrasting filters (in order of damping coefficient, from lower to higher values): Gaussian, Bessel, linear phase, Butterworth, Chebyshev, Legendre, elliptic. (with graphs).
- USING THE ANALOG DEVICES ACTIVE FILTER DESIGN TOOL: a similar application note from Analog DevicesAnalog DevicesAnalog Devices, Inc. , known as ADI, is an American multinational semiconductor company specializing in data conversion and signal conditioning technology, headquartered in Norwood, Massachusetts...
with extensive graphs, active RC filter topologies, and tables for practical design. - "Design and Analysis of Analog Filters: A Signal Processing Perspective" by L. D. Paarmann