
Matched filter
Encyclopedia
In telecommunication
s, a matched filter (originally known as a North filter) is obtained by correlating
a known signal
, or template
, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving
the unknown signal with a conjugated
time-reversed version of the template. The matched filter is the optimal linear filter
for maximizing the signal to noise ratio (SNR) in the presence of additive stochastic noise
. Matched filters are commonly used in radar
, in which a known signal is sent out, and the reflected signal is examined for common elements of the out-going signal. Pulse compression
is an example of matched filtering. Two-dimensional matched filters are commonly used in image processing
, e.g., to improve SNR for X-ray pictures.
The matched filter is the linear filter, , that maximizes the output signal-to-noise ratio
, that maximizes the output signal-to-noise ratio
.

Though we most often express filters as the impulse response
of convolution systems, as above (see LTI system theory
), it is easiest to think of the matched filter in the context of the inner product, which we will see shortly.
We can derive the linear filter that maximizes output signal-to-noise ratio by invoking a geometric argument. The intuition behind the matched filter relies on correlating the received signal (a vector) with a filter (another vector) that is parallel with the signal, maximizing the inner product. This enhances the signal. When we consider the additive stochastic noise, we have the additional challenge of minimizing the output due to noise by choosing a filter that is orthogonal to the noise.
Let us formally define the problem. We seek a filter, , such that we maximize the output signal-to-noise ratio, where the output is the inner product of the filter and the observed signal
, such that we maximize the output signal-to-noise ratio, where the output is the inner product of the filter and the observed signal  .
.
Our observed signal consists of the desirable signal and additive noise
and additive noise  :
:
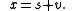
Let us define the covariance matrix of the noise, reminding ourselves that this matrix has Hermitian symmetry, a property that will become useful in the derivation:

where denotes Hermitian (conjugate) transpose
denotes Hermitian (conjugate) transpose
, and denotes expectation
denotes expectation
.
Let us call our output,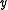 , the inner product of our filter and the observed signal such that
, the inner product of our filter and the observed signal such that
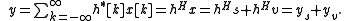
We now define the signal-to-noise ratio, which is our objective function, to be the ratio of the power of the output due to the desired signal to the power of the output due to the noise:
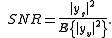
We rewrite the above:

We wish to maximize this quantity by choosing . Expanding the denominator of our objective function, we have
. Expanding the denominator of our objective function, we have
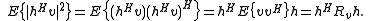
Now, our becomes
becomes

We will rewrite this expression with some matrix manipulation. The reason for this seemingly counterproductive measure will become evident shortly. Exploiting the Hermitian symmetry of the covariance matrix , we can write
, we can write

We would like to find an upper bound on this expression. To do so, we first recognize a form of the Cauchy-Schwarz inequality:

which is to say that the square of the inner product of two vectors can only be as large as the product of the individual inner products of the vectors. This concept returns to the intuition behind the matched filter: this upper bound is achieved when the two vectors and
and  are parallel. We resume our derivation by expressing the upper bound on our
are parallel. We resume our derivation by expressing the upper bound on our 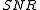 in light of the geometric inequality above:
in light of the geometric inequality above:

Our valiant matrix manipulation has now paid off. We see that the expression for our upper bound can be greatly simplified:
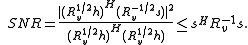
We can achieve this upper bound if we choose,

where is an arbitrary real number. To verify this, we plug into our expression for the output
is an arbitrary real number. To verify this, we plug into our expression for the output  :
:
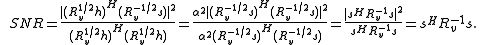
Thus, our optimal matched filter is
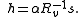
We often choose to normalize the expected value of the power of the filter output due to the noise to unity. That is, we constrain
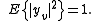
This constraint implies a value of , for which we can solve:
, for which we can solve:

yielding
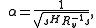
giving us our normalized filter,

If we care to write the impulse response of the filter for the convolution system, it is simply the complex conjugate time reversal of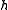 .
.
Though we have derived the matched filter in discrete time, we can extend the concept to continuous-time systems if we replace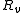 with the continuous-time autocorrelation
with the continuous-time autocorrelation
function of the noise, assuming a continuous signal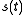 , continuous noise
, continuous noise 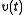 , and a continuous filter
, and a continuous filter 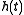 .
.
 ) of a filtered deterministic signal in stochastic additive noise. The observed sequence, again, is
) of a filtered deterministic signal in stochastic additive noise. The observed sequence, again, is

with the noise covariance matrix,

The signal-to-noise ratio is
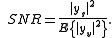
Evaluating the expression in the numerator, we have
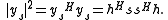
and in the denominator,
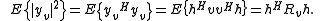
The signal-to-noise ratio becomes

If we now constrain the denominator to be 1, the problem of maximizing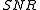 is reduced to maximizing the numerator. We can then formulate the problem using a Lagrange multiplier
is reduced to maximizing the numerator. We can then formulate the problem using a Lagrange multiplier
:

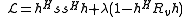

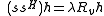
which we recognize as an eigenvalue problem

Since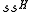 is of unit rank, it has only one nonzero eigenvalue. It can be shown that this eigenvalue equals
is of unit rank, it has only one nonzero eigenvalue. It can be shown that this eigenvalue equals

yielding the following optimal matched filter
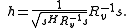
This is the same result found in the previous section.
and digital communications, where the original waveform is known and the objective is to detect the presence of this signal against the background noise.
). As an example, suppose that we wish to judge the distance of an object by reflecting a signal off it. We may choose to transmit a pure-tone sinusoid at 1 Hz. We assume that our received signal is an attenuated and phase-shifted form of the transmitted signal with added noise.
To judge the distance of the object, we correlate the received signal with a matched filter, which, in the case of white (uncorrelated) noise
, is another pure-tone 1-Hz sinusoid. When the output of the matched filter system exceeds a certain threshold, we conclude with high probability that the received signal has been reflected off the object. Using the speed of propagation and the time that we first observe the reflected signal, we can estimate the distance of the object. If we change the shape of the pulse in a specially-designed way, the signal-to-noise ratio and the distance resolution can be even improved after matched filtering: this is a technique known as pulse compression
.
Additionally, matched filters can be used in parameter estimation problems (see estimation theory
). To return to our previous example, we may desire to estimate the speed of the object, in addition to its position. To exploit the Doppler effect
, we would like to estimate the frequency of the received signal. To do so, we may correlate the received signal with several matched filters of sinusoids at varying frequencies. The matched filter with the highest output will reveal, with high probability, the frequency of the reflected signal and help us determine the speed of the object. This method is, in fact, a simple version of the discrete Fourier transform (DFT)
. The DFT takes an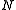 -valued complex input and correlates it with
-valued complex input and correlates it with 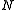 matched filters, corresponding to complex exponentials at
matched filters, corresponding to complex exponentials at 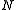 different frequencies, to yield
different frequencies, to yield 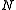 complex-valued numbers corresponding to the relative amplitudes and phases of the sinusoidal components (see Moving target indication
complex-valued numbers corresponding to the relative amplitudes and phases of the sinusoidal components (see Moving target indication
).

Imagine we want to send the sequence "0101100100" coded in non polar Non-return-to-zero
(NRZ) through a certain channel.
Mathematically, a sequence in NRZ code can be described as a sequence of unit pulses or shifted rect functions, each pulse being weighted by +1 if the bit is "1" and by 0 if the bit is "0". Formally, the scaling factor for the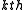 bit is,
bit is,
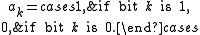
We can represent our message,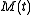 , as the sum of shifted unit pulses:
, as the sum of shifted unit pulses:
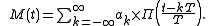
where is the time length of one bit.
is the time length of one bit.
Thus, the signal to be sent by the transmitter is

If we model our noisy channel as an AWGN channel, white Gaussian noise is added to the signal. At the receiver end, for a Signal-to-noise ratio of 3dB, this may look like:

A first glance will not reveal the original transmitted sequence. There is a high power of noise relative to the power of the desired signal (i.e., there is a low signal-to-noise ratio
). If the receiver were to sample this signal at the correct moments, the resulting binary message would possibly belie the original transmitted one.
To increase our signal-to-noise ratio, we pass the received signal through a matched filter. In this case, the filter should be matched to an NRZ pulse (equivalent to a "1" coded in NRZ code). Precisely, the impulse response of the ideal matched filter, assuming white (uncorrelated) noise should be a time-reversed complex-conjugated scaled version of the signal that we are seeking. We choose
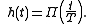
In this case, due to symmetry, the time-reversed complex conjugate of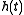 is in fact
is in fact  , allowing us to call
, allowing us to call  the impulse response of our matched filter convolution system.
the impulse response of our matched filter convolution system.
After convolving with the correct matched filter, the resulting signal, is,
is,
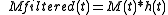
where denotes convolution.
denotes convolution.

Which can now be safely sampled by the receiver at the correct sampling instants, and compared to an appropriate threshold, resulting in a correct interpretation of the binary message.

Telecommunication
Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
s, a matched filter (originally known as a North filter) is obtained by correlating
Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
a known signal
Signal (electrical engineering)
In the fields of communications, signal processing, and in electrical engineering more generally, a signal is any time-varying or spatial-varying quantity....
, or template
Template
Template may mean:*a stencil, pattern or overlay used in graphic arts and sewing to replicate letters, shapes or designs...
, with an unknown signal to detect the presence of the template in the unknown signal. This is equivalent to convolving
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
the unknown signal with a conjugated
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
time-reversed version of the template. The matched filter is the optimal linear filter
Linear filter
Linear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
for maximizing the signal to noise ratio (SNR) in the presence of additive stochastic noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
. Matched filters are commonly used in radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
, in which a known signal is sent out, and the reflected signal is examined for common elements of the out-going signal. Pulse compression
Pulse compression
Pulse compression is a signal processing technique mainly used in radar, sonar and echography to increase the range resolution as well as the signal to noise ratio...
is an example of matched filtering. Two-dimensional matched filters are commonly used in image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, e.g., to improve SNR for X-ray pictures.
Derivation of the matched filter
The following section derives the matched filter for a discrete-time system. The derivation for a continuous-time system is similar, with summations replaced with integrals.The matched filter is the linear filter,
 , that maximizes the output signal-to-noise ratio
, that maximizes the output signal-to-noise ratioSignal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
.

Though we most often express filters as the impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of convolution systems, as above (see LTI system theory
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
), it is easiest to think of the matched filter in the context of the inner product, which we will see shortly.
We can derive the linear filter that maximizes output signal-to-noise ratio by invoking a geometric argument. The intuition behind the matched filter relies on correlating the received signal (a vector) with a filter (another vector) that is parallel with the signal, maximizing the inner product. This enhances the signal. When we consider the additive stochastic noise, we have the additional challenge of minimizing the output due to noise by choosing a filter that is orthogonal to the noise.
Let us formally define the problem. We seek a filter,
 , such that we maximize the output signal-to-noise ratio, where the output is the inner product of the filter and the observed signal
, such that we maximize the output signal-to-noise ratio, where the output is the inner product of the filter and the observed signal  .
.Our observed signal consists of the desirable signal
 and additive noise
and additive noise  :
: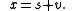
Let us define the covariance matrix of the noise, reminding ourselves that this matrix has Hermitian symmetry, a property that will become useful in the derivation:

where
 denotes Hermitian (conjugate) transpose
denotes Hermitian (conjugate) transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
, and
 denotes expectation
denotes expectationExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
.
Let us call our output,
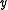 , the inner product of our filter and the observed signal such that
, the inner product of our filter and the observed signal such that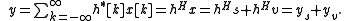
We now define the signal-to-noise ratio, which is our objective function, to be the ratio of the power of the output due to the desired signal to the power of the output due to the noise:
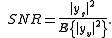
We rewrite the above:

We wish to maximize this quantity by choosing
 . Expanding the denominator of our objective function, we have
. Expanding the denominator of our objective function, we have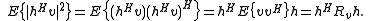
Now, our
 becomes
becomes
We will rewrite this expression with some matrix manipulation. The reason for this seemingly counterproductive measure will become evident shortly. Exploiting the Hermitian symmetry of the covariance matrix
 , we can write
, we can write
We would like to find an upper bound on this expression. To do so, we first recognize a form of the Cauchy-Schwarz inequality:

which is to say that the square of the inner product of two vectors can only be as large as the product of the individual inner products of the vectors. This concept returns to the intuition behind the matched filter: this upper bound is achieved when the two vectors
 and
and  are parallel. We resume our derivation by expressing the upper bound on our
are parallel. We resume our derivation by expressing the upper bound on our 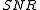 in light of the geometric inequality above:
in light of the geometric inequality above:
Our valiant matrix manipulation has now paid off. We see that the expression for our upper bound can be greatly simplified:
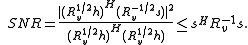
We can achieve this upper bound if we choose,

where
 is an arbitrary real number. To verify this, we plug into our expression for the output
is an arbitrary real number. To verify this, we plug into our expression for the output  :
: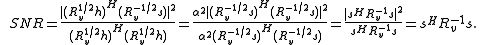
Thus, our optimal matched filter is
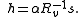
We often choose to normalize the expected value of the power of the filter output due to the noise to unity. That is, we constrain
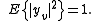
This constraint implies a value of
 , for which we can solve:
, for which we can solve:
yielding
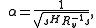
giving us our normalized filter,

If we care to write the impulse response of the filter for the convolution system, it is simply the complex conjugate time reversal of
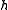 .
.Though we have derived the matched filter in discrete time, we can extend the concept to continuous-time systems if we replace
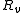 with the continuous-time autocorrelation
with the continuous-time autocorrelationAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
function of the noise, assuming a continuous signal
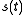 , continuous noise
, continuous noise 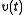 , and a continuous filter
, and a continuous filter 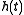 .
.Alternative derivation of the matched filter
Alternatively, we may solve for the matched filter by solving our maximization problem with a Lagrangian. Again, the matched filter endeavors to maximize the output signal-to-noise ratio ( ) of a filtered deterministic signal in stochastic additive noise. The observed sequence, again, is
) of a filtered deterministic signal in stochastic additive noise. The observed sequence, again, is
with the noise covariance matrix,

The signal-to-noise ratio is
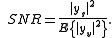
Evaluating the expression in the numerator, we have
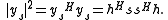
and in the denominator,
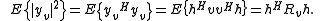
The signal-to-noise ratio becomes

If we now constrain the denominator to be 1, the problem of maximizing
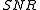 is reduced to maximizing the numerator. We can then formulate the problem using a Lagrange multiplier
is reduced to maximizing the numerator. We can then formulate the problem using a Lagrange multiplierLagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
:

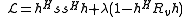

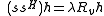
which we recognize as an eigenvalue problem

Since
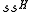 is of unit rank, it has only one nonzero eigenvalue. It can be shown that this eigenvalue equals
is of unit rank, it has only one nonzero eigenvalue. It can be shown that this eigenvalue equals
yielding the following optimal matched filter
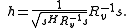
This is the same result found in the previous section.
Frequency-domain interpretation
When viewed in the frequency domain, it is evident that the matched filter applies the greatest weighting to spectral components that have the greatest signal-to-noise ratio. Although in general this requires a non-flat frequency response, the associated distortion is not significant in situations such as radarRadar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
and digital communications, where the original waveform is known and the objective is to detect the presence of this signal against the background noise.
Example of matched filter in radar and sonar
Matched filters are often used in signal detection (see detection theoryDetection theory
Detection theory, or signal detection theory, is a means to quantify the ability to discern between information-bearing energy patterns and random energy patterns that distract from the information Detection theory, or signal detection theory, is a means to quantify the ability to discern between...
). As an example, suppose that we wish to judge the distance of an object by reflecting a signal off it. We may choose to transmit a pure-tone sinusoid at 1 Hz. We assume that our received signal is an attenuated and phase-shifted form of the transmitted signal with added noise.
To judge the distance of the object, we correlate the received signal with a matched filter, which, in the case of white (uncorrelated) noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
, is another pure-tone 1-Hz sinusoid. When the output of the matched filter system exceeds a certain threshold, we conclude with high probability that the received signal has been reflected off the object. Using the speed of propagation and the time that we first observe the reflected signal, we can estimate the distance of the object. If we change the shape of the pulse in a specially-designed way, the signal-to-noise ratio and the distance resolution can be even improved after matched filtering: this is a technique known as pulse compression
Pulse compression
Pulse compression is a signal processing technique mainly used in radar, sonar and echography to increase the range resolution as well as the signal to noise ratio...
.
Additionally, matched filters can be used in parameter estimation problems (see estimation theory
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
). To return to our previous example, we may desire to estimate the speed of the object, in addition to its position. To exploit the Doppler effect
Doppler effect
The Doppler effect , named after Austrian physicist Christian Doppler who proposed it in 1842 in Prague, is the change in frequency of a wave for an observer moving relative to the source of the wave. It is commonly heard when a vehicle sounding a siren or horn approaches, passes, and recedes from...
, we would like to estimate the frequency of the received signal. To do so, we may correlate the received signal with several matched filters of sinusoids at varying frequencies. The matched filter with the highest output will reveal, with high probability, the frequency of the reflected signal and help us determine the speed of the object. This method is, in fact, a simple version of the discrete Fourier transform (DFT)
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
. The DFT takes an
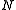 -valued complex input and correlates it with
-valued complex input and correlates it with 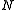 matched filters, corresponding to complex exponentials at
matched filters, corresponding to complex exponentials at 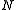 different frequencies, to yield
different frequencies, to yield 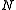 complex-valued numbers corresponding to the relative amplitudes and phases of the sinusoidal components (see Moving target indication
complex-valued numbers corresponding to the relative amplitudes and phases of the sinusoidal components (see Moving target indicationMoving target indication
Moving target indication is a mode of operation of a radar to discriminate a target against clutter. In contrast to another mode, stationary target indication, it takes an advantage of the fact that the target moves with respect to stationary clutter. The most common approach takes advantage of...
).
Example of matched filter in digital communications
The matched filter is also used in communications. In the context of a communication system that sends binary messages from the transmitter to the receiver across a noisy channel, a matched filter can be used to detect the transmitted pulses in the noisy received signal.
Imagine we want to send the sequence "0101100100" coded in non polar Non-return-to-zero
Non-return-to-zero
In telecommunication, a non-return-to-zero line code is a binary code in which 1's are represented by one significant condition and 0's are represented by some other significant condition , with no other neutral or rest condition. The pulses have more energy than a RZ code...
(NRZ) through a certain channel.
Mathematically, a sequence in NRZ code can be described as a sequence of unit pulses or shifted rect functions, each pulse being weighted by +1 if the bit is "1" and by 0 if the bit is "0". Formally, the scaling factor for the
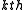 bit is,
bit is,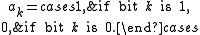
We can represent our message,
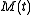 , as the sum of shifted unit pulses:
, as the sum of shifted unit pulses: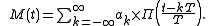
where
 is the time length of one bit.
is the time length of one bit.Thus, the signal to be sent by the transmitter is

If we model our noisy channel as an AWGN channel, white Gaussian noise is added to the signal. At the receiver end, for a Signal-to-noise ratio of 3dB, this may look like:

A first glance will not reveal the original transmitted sequence. There is a high power of noise relative to the power of the desired signal (i.e., there is a low signal-to-noise ratio
Signal-to-noise ratio
Signal-to-noise ratio is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. It is defined as the ratio of signal power to the noise power. A ratio higher than 1:1 indicates more signal than noise...
). If the receiver were to sample this signal at the correct moments, the resulting binary message would possibly belie the original transmitted one.
To increase our signal-to-noise ratio, we pass the received signal through a matched filter. In this case, the filter should be matched to an NRZ pulse (equivalent to a "1" coded in NRZ code). Precisely, the impulse response of the ideal matched filter, assuming white (uncorrelated) noise should be a time-reversed complex-conjugated scaled version of the signal that we are seeking. We choose
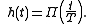
In this case, due to symmetry, the time-reversed complex conjugate of
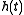 is in fact
is in fact  , allowing us to call
, allowing us to call  the impulse response of our matched filter convolution system.
the impulse response of our matched filter convolution system.After convolving with the correct matched filter, the resulting signal,
 is,
is,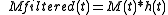
where
 denotes convolution.
denotes convolution.
Which can now be safely sampled by the receiver at the correct sampling instants, and compared to an appropriate threshold, resulting in a correct interpretation of the binary message.


