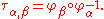Atlas (topology)
Encyclopedia
In mathematics
, particularly topology
, one describes
a manifold
using an atlas. An atlas consists of individual
charts that, roughly speaking, describe individual regions
of the manifold. If the manifold is the surface of the Earth,
then an atlas has its more common meaning. In general,
the notion of atlas underlies the formal definition of a manifold
.
A chart for a topological space
M is a homeomorphism
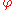from an open subset
U of M to an open subset of Euclidean space
. The chart is traditionally recorded as the ordered pair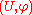
.
M is a collection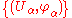
of charts on M such that
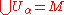. If the range of each chart is the n-dimensional Euclidean space
, then M is said to be an n-dimensional manifold
.
To make this comparison, we consider the composition of one chart
with the inverse of the other. This composition is not well-defined
unless we restrict both charts to the intersection of their domains
of definition. (For example, if we have a chart of Europe and a chart of Russia, then we can compare these two charts on their overlap, namely the European part of Russia.)
To be more precise, suppose that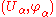
and 
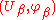are two charts for a manifold M such that 
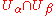is non-empty.
The transition map
is the map defined on the intersection
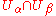by
Note that since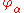
and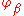 
are both homeomorphisms, the transition map 
is also a homeomorphism.
of functions on a manifold, then it is necessary to construct an atlas
whose transition functions are differentiable. Then one
can unambiguously define the notion of tangent vectors
and then directional derivative
s.
If each transition function
is a smooth map, then the atlas is called a
smooth atlas
.
Alternatively, one could require that the transition maps
have only k continuous derivatives in which case the atlas is
said to be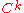
.
Very generally, if each transition function
belongs to a pseudo-group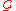
of homeomorphism
s of Euclidean space
,
then the atlas is called a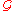
-atlas.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, one describes
a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
using an atlas. An atlas consists of individual
charts that, roughly speaking, describe individual regions
of the manifold. If the manifold is the surface of the Earth,
then an atlas has its more common meaning. In general,
the notion of atlas underlies the formal definition of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
Charts
The definition of an atlas depends on the notion of a chart.A chart for a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
M is a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
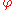from an open subsetOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
U of M to an open subset of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The chart is traditionally recorded as the ordered pair
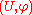.Formal defintion of atlas
An atlas for a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
M is a collection
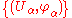of charts on M such that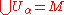. If the range of each chart is the n-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, then M is said to be an n-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
.
Transition maps
A transition map provides a way of comparing two charts of an atlas.To make this comparison, we consider the composition of one chart
with the inverse of the other. This composition is not well-defined
unless we restrict both charts to the intersection of their domains
of definition. (For example, if we have a chart of Europe and a chart of Russia, then we can compare these two charts on their overlap, namely the European part of Russia.)
To be more precise, suppose that
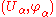and 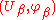are two charts for a manifold M such that 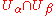is non-empty.The transition map
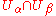is the map defined on the intersection by
Note that since
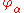and 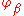are both homeomorphisms, the transition map is also a homeomorphism.More structure
One often desires more structure on a manifold than simply the topological structure. For example, if one would like an unambiguous notion of differentiationDifferentiation
Differentiation may refer to:* Differentiation , the process of finding a derivative* Differentiated instruction in education* Cellular differentiation in biology* Planetary differentiation in planetary science...
of functions on a manifold, then it is necessary to construct an atlas
whose transition functions are differentiable. Then one
can unambiguously define the notion of tangent vectors
and then directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
s.
If each transition function
is a smooth map, then the atlas is called a
smooth atlas
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
.
Alternatively, one could require that the transition maps
have only k continuous derivatives in which case the atlas is
said to be
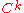.Very generally, if each transition function
belongs to a pseudo-group
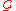
of homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
,
then the atlas is called a
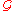-atlas.