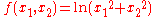Harmonic function
Encyclopedia
In mathematics
, mathematical physics
and the theory of stochastic process
es, a harmonic function is a twice continuously differentiable
function
f : U → R (where U is an open subset
of Rn) which satisfies Laplace's equation
, i.e.
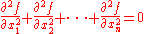
everywhere on U. This is usually written as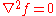
or
Examples of harmonic functions of three variables are given in the table below with :
:
Finally, examples of harmonic functions of n variables are:
Δ and is therefore a vector space
over R: sums, differences and scalar multiples of harmonic functions are again harmonic.
If f is a harmonic function on U, then all partial derivative
s of f are also harmonic functions on U. The Laplace operator Δ and the partial derivative operator will commute on this class of functions.
In several ways, the harmonic functions are real analogues to holomorphic function
s. All harmonic functions are analytic
, i.e. they can be locally expressed as power series. This is a general fact about elliptic operator
s, of which the Laplacian is a major example.
The uniform limit of a convergent sequence of harmonic functions is still harmonic. This is true because any continuous function satisfying the mean value property is harmonic. Consider the sequence on ( , 0)× R defined by
, 0)× R defined by 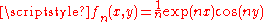 . This sequence is harmonic and converges uniformly to the zero function; however note that the partial derivatives are not uniformly convergent to the zero function (the derivative of the zero function). This example shows the importance of relying on the mean value property and continuity to argue that the limit is harmonic.
. This sequence is harmonic and converges uniformly to the zero function; however note that the partial derivatives are not uniformly convergent to the zero function (the derivative of the zero function). This example shows the importance of relying on the mean value property and continuity to argue that the limit is harmonic.
functions). Conversely, any harmonic function on an open set
on an open set  is locally the real part of a holomorphic function. This is immediately seen observing that, writing
is locally the real part of a holomorphic function. This is immediately seen observing that, writing  the complex function
the complex function 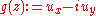 is holomorphic in
is holomorphic in 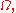 because it satisfies the Cauchy-Riemann equations
because it satisfies the Cauchy-Riemann equations
. Therefore, g has locally a primitive , and
, and  is the real part of
is the real part of  up to a constant, as
up to a constant, as 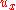 is the real part of
is the real part of 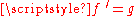 .
.
Although the above correspondence with holomorphic functions only holds for functions of two real variables, still harmonic functions in n variables enjoy a number of properties typical of holomorphic functions. They are (real) analytic; they have a maximum principle and a mean-value principle; a theorem of removal of singularities as well as a Liouville theorem one holds for them in analogy to the corresponding theorems in complex functions theory.
.
: if K is any compact subset
of U, then f, restricted to K, attains its maximum and minimum
on the boundary
of K. If U is connected
, this means that f cannot have local maxima or minima, other than the exceptional case where f is constant
. Similar properties can be shown for subharmonic functions.
with center x and radius r which is completely contained in the open set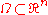 , then the value
, then the value 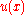 of a harmonic function
of a harmonic function 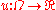 at the center of the ball is given by the average value of
at the center of the ball is given by the average value of  on the surface of the ball; this average value is also equal to the average value of
on the surface of the ball; this average value is also equal to the average value of  in the interior of the ball. In other words
in the interior of the ball. In other words
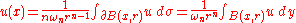
where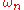 is the volume of the unit ball in n dimensions and
is the volume of the unit ball in n dimensions and  is the n-1 dimensional surface measure .
is the n-1 dimensional surface measure .
Conversely, all locally integrable functions satisfying the (volume) mean-value property are infinitely differentiable and harmonic functions as well.
In terms of convolution
s, if
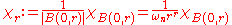
denotes the characteristic function
of the ball with radius r about the origin, normalized so that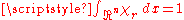 , the function
, the function  is harmonic on
is harmonic on  if and only if
if and only if
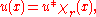
as soon as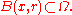
Sketch of the proof. The proof of the mean-value property of the harmonic functions and its converse follows immediately observing that the non-homogeneous equation, for any

admits an easy explicit solution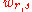 of class
of class 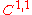 with compact support in
with compact support in 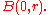 Thus, if
Thus, if  is harmonic in
is harmonic in 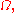
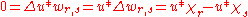
holds in the set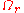 of all points
of all points  with
with  .
.
Since is continuous in
is continuous in 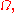
 converges to
converges to  as
as  showing the mean value property for
showing the mean value property for  in
in  Conversely, if u is any
Conversely, if u is any 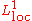 function satisfying the mean-value property in
function satisfying the mean-value property in  , that is,
, that is,
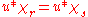
holds in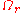 for all
for all  then, iterating m times the convolution with
then, iterating m times the convolution with  one has:
one has:

so that is
is 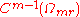 because the m-fold iterated convolution of
because the m-fold iterated convolution of  is of class
is of class 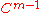 with support
with support  Since
Since  and
and  are arbitrary,
are arbitrary, is
is 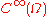 too. Moreover
too. Moreover

for all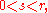 so that
so that  in
in  by the fundamental theorem of the calculus of variations, proving the equivalence between harmonicity and mean-value property.
by the fundamental theorem of the calculus of variations, proving the equivalence between harmonicity and mean-value property.
This statement of the mean value property can be generalized as follows: If h is any spherically symmetric function supported
in B(x,r) such that ∫h = 1, then u(x) = h * u(x). In other words, we can take the weighted average of u about a point and recover u(x). In particular, by taking h to be a C∞ function, we can recover the value of u at any point even if we only know how u acts as a distribution
. See Weyl's lemma
.
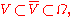
Harnack's inequality

holds for some constant C that depends only on V and Ω.
 of Rn, which is less singular at
of Rn, which is less singular at  than the fundamental solution, that is
than the fundamental solution, that is

then f extends to a harmonic function on (compare Riemann's theorem for functions of a complex variable).
(compare Riemann's theorem for functions of a complex variable).
).
Edward Nelson
gave a particularly short proof of this theorem, using the mean value property mentioned above:
) is weakly harmonic
if it satisfies Laplace's equation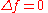
in a weak
sense (or, equivalently, in the sense of distributions). A weakly harmonic function coincides almost everywhere with a strongly harmonic function, and is in particular smooth. A weakly harmonic distribution is precisely the distribution associated to a strongly harmonic function, and so also is smooth. This is Weyl's lemma
.
There are other weak formulation
s of Laplace's equation that are often useful. One of which is Dirichlet's principle, representing harmonic functions in the Sobolev space
H1(Ω) as the minimizers of the Dirichlet energy
integral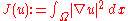
with respect to local variations, that is, all functions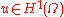 such that
such that 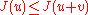 holds for all
holds for all 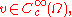 or equivalently, for all
or equivalently, for all 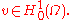
, using the Laplace-Beltrami operator
Δ. In this context, a function is called harmonic if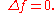
Many of the properties of harmonic functions on domains in Euclidean space carry over to this more general setting, including the mean value theorem (over geodesic
balls), the maximum principle, and the Harnack inequality. With the exception of the mean value theorem, these are easy consequences of the corresponding results for general linear elliptic partial differential equations of the second order.
 is called subharmonic. This condition guarantees that the maximum principle will hold, although other properties of harmonic functions may fail. More generally, a function is subharmonic if and only if, in the interior of any ball in its domain, its graph lies below that of the harmonic function interpolating its boundary values on the ball.
is called subharmonic. This condition guarantees that the maximum principle will hold, although other properties of harmonic functions may fail. More generally, a function is subharmonic if and only if, in the interior of any ball in its domain, its graph lies below that of the harmonic function interpolating its boundary values on the ball.
s, and it is related to the study of cohomology
. Also, it is possible to define harmonic vector-valued functions, or harmonic maps of two Riemannian manifolds, which are critical points of a generalized Dirichlet energy functional (this includes harmonic functions as a special case, a result known as Dirichlet principle). These kind of harmonic maps appear in the theory of minimal surfaces. For example, a curve, that is, a map from an interval in R to a Riemannian manifold, is a harmonic map if and only if it is a geodesic
.
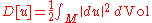
in which is the differential of u, and the norm is that induced by the metric on M and that on N on the tensor product bundle T∗M⊗u−1TN.
Important special cases of harmonic maps between manifolds include minimal surface
s, which are precisely the harmonic immersions of a surface into three-dimensional Euclidean space. More generally, minimal submanifolds are harmonic immersions of one manifold in another. Harmonic coordinates
are a harmonic diffeomorphism
from a manifold to an open subset of a Euclidean space of the same dimension.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
and the theory of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es, a harmonic function is a twice continuously differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : U → R (where U is an open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of Rn) which satisfies Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
, i.e.
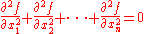
everywhere on U. This is usually written as
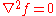
or

Examples
Examples of harmonic functions of two variables are:- The real and imaginary part of any holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
- The function
-
- defined on
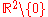 (e.g. the electric potential due to a line charge, and the gravity potential due to a long cylindrical mass)
(e.g. the electric potential due to a line charge, and the gravity potential due to a long cylindrical mass)
- The function
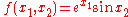
- The function
Examples of harmonic functions of three variables are given in the table below with
 :
:| Function | Singularity |
|---|---|
 |
Unit point charge at origin |
 |
x-directed dipole at origin |
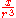 |
Line of unit charge density on entire z-axis |
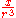 |
Line of unit charge density on negative z-axis |
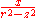 |
Line of x-directed dipoles on entire z axis |
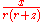 |
Line of x-directed dipoles on negative z axis |
- Harmonic functions are determined by their singularities. The singular points of the harmonic functions above are expressed as "charges" and "charge densities" using the terminology of electrostatics, and so the corresponding harmonic function will be proportional to the electrostatic potential due to these charge distributions. Each function above will yield another harmonic function when multiplied by a constant, rotated, and/or has a constant added. The inversion of each function will yield another harmonic function which has singularities which are the images of the original singularities in a spherical "mirror". Also, the sum of any two harmonic functions will yield another harmonic function.
Finally, examples of harmonic functions of n variables are:
- The constant, linear and affine functions on all of
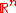 (for example, the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
(for example, the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
between the plates of a capacitorCapacitorA capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
, and the gravity potential of a slab) - The function
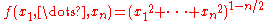 on
on 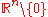 for
for  .
.
Remarks
The set of harmonic functions on a given open set U can be seen as the kernel of the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
Δ and is therefore a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over R: sums, differences and scalar multiples of harmonic functions are again harmonic.
If f is a harmonic function on U, then all partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of f are also harmonic functions on U. The Laplace operator Δ and the partial derivative operator will commute on this class of functions.
In several ways, the harmonic functions are real analogues to holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s. All harmonic functions are analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, i.e. they can be locally expressed as power series. This is a general fact about elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
s, of which the Laplacian is a major example.
The uniform limit of a convergent sequence of harmonic functions is still harmonic. This is true because any continuous function satisfying the mean value property is harmonic. Consider the sequence on (
 , 0)× R defined by
, 0)× R defined by 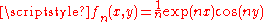 . This sequence is harmonic and converges uniformly to the zero function; however note that the partial derivatives are not uniformly convergent to the zero function (the derivative of the zero function). This example shows the importance of relying on the mean value property and continuity to argue that the limit is harmonic.
. This sequence is harmonic and converges uniformly to the zero function; however note that the partial derivatives are not uniformly convergent to the zero function (the derivative of the zero function). This example shows the importance of relying on the mean value property and continuity to argue that the limit is harmonic.Connections with complex function theory
The real and imaginary part of any holomorphic function yield harmonic functions on R2 (these are said to be a pair of harmonic conjugateHarmonic conjugate
In mathematics, a function u defined on some open domain \Omega\subset\R^2 is said to have as a conjugate a function v if and only if they are respectively real and imaginary part of a holomorphic function f of the complex variable z:=x+iy\in\Omega. That is, v is conjugated to u if f:=u+iv is...
functions). Conversely, any harmonic function
 on an open set
on an open set  is locally the real part of a holomorphic function. This is immediately seen observing that, writing
is locally the real part of a holomorphic function. This is immediately seen observing that, writing  the complex function
the complex function 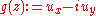 is holomorphic in
is holomorphic in 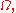 because it satisfies the Cauchy-Riemann equations
because it satisfies the Cauchy-Riemann equationsCauchy-Riemann equations
In mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...
. Therefore, g has locally a primitive
 , and
, and  is the real part of
is the real part of  up to a constant, as
up to a constant, as 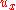 is the real part of
is the real part of 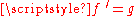 .
.Although the above correspondence with holomorphic functions only holds for functions of two real variables, still harmonic functions in n variables enjoy a number of properties typical of holomorphic functions. They are (real) analytic; they have a maximum principle and a mean-value principle; a theorem of removal of singularities as well as a Liouville theorem one holds for them in analogy to the corresponding theorems in complex functions theory.
Properties of harmonic functions
Some important properties of harmonic functions can be deduced from Laplace's equation.Regularity theorem for harmonic functions
Harmonic functions are infinitely differentiable. In fact, harmonic functions are real analyticAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
.
Maximum principle
Harmonic functions satisfy the following maximum principleMaximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
: if K is any compact subset
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
of U, then f, restricted to K, attains its maximum and minimum
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of K. If U is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, this means that f cannot have local maxima or minima, other than the exceptional case where f is constant
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
. Similar properties can be shown for subharmonic functions.
The mean value property
If B(x,r) is a ballBall (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
with center x and radius r which is completely contained in the open set
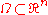 , then the value
, then the value 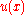 of a harmonic function
of a harmonic function 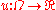 at the center of the ball is given by the average value of
at the center of the ball is given by the average value of  on the surface of the ball; this average value is also equal to the average value of
on the surface of the ball; this average value is also equal to the average value of  in the interior of the ball. In other words
in the interior of the ball. In other words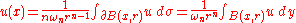
where
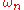 is the volume of the unit ball in n dimensions and
is the volume of the unit ball in n dimensions and  is the n-1 dimensional surface measure .
is the n-1 dimensional surface measure .Conversely, all locally integrable functions satisfying the (volume) mean-value property are infinitely differentiable and harmonic functions as well.
In terms of convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
s, if
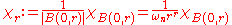
denotes the characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of the ball with radius r about the origin, normalized so that
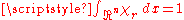 , the function
, the function  is harmonic on
is harmonic on  if and only if
if and only if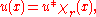
as soon as
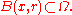
Sketch of the proof. The proof of the mean-value property of the harmonic functions and its converse follows immediately observing that the non-homogeneous equation, for any


admits an easy explicit solution
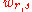 of class
of class 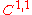 with compact support in
with compact support in 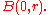 Thus, if
Thus, if  is harmonic in
is harmonic in 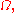
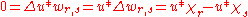
holds in the set
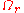 of all points
of all points  with
with  .
.Since
 is continuous in
is continuous in 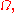
 converges to
converges to  as
as  showing the mean value property for
showing the mean value property for  in
in  Conversely, if u is any
Conversely, if u is any 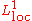 function satisfying the mean-value property in
function satisfying the mean-value property in  , that is,
, that is,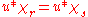
holds in
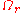 for all
for all  then, iterating m times the convolution with
then, iterating m times the convolution with  one has:
one has:
so that
 is
is 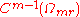 because the m-fold iterated convolution of
because the m-fold iterated convolution of  is of class
is of class 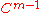 with support
with support  Since
Since  and
and  are arbitrary,
are arbitrary, is
is 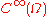 too. Moreover
too. Moreover
for all
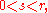 so that
so that  in
in  by the fundamental theorem of the calculus of variations, proving the equivalence between harmonicity and mean-value property.
by the fundamental theorem of the calculus of variations, proving the equivalence between harmonicity and mean-value property.This statement of the mean value property can be generalized as follows: If h is any spherically symmetric function supported
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
in B(x,r) such that ∫h = 1, then u(x) = h * u(x). In other words, we can take the weighted average of u about a point and recover u(x). In particular, by taking h to be a C∞ function, we can recover the value of u at any point even if we only know how u acts as a distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
. See Weyl's lemma
Weyl's lemma (Laplace equation)
In mathematics, Weyl's lemma is a result that provides a "very weak" form of the Laplace equation. It is named after the German mathematician Hermann Weyl.-Statement of the lemma:...
.
Harnack's inequality
Let u be a non-negative harmonic function in a bounded domain Ω. Then for every connected set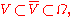
Harnack's inequality
Harnack's inequality
In mathematics, Harnack's inequality is an inequality relating the values of a positive harmonic function at two points, introduced by . and generalized Harnack's inequality to solutions of elliptic or parabolic partial differential equations. Perelman's solution of the Poincaré conjecture uses...

holds for some constant C that depends only on V and Ω.
Removal of singularities
The following principle of removal of singularities holds for harmonic functions. If f is a harmonic function defined on a dotted open subset of Rn, which is less singular at
of Rn, which is less singular at  than the fundamental solution, that is
than the fundamental solution, that is
then f extends to a harmonic function on
 (compare Riemann's theorem for functions of a complex variable).
(compare Riemann's theorem for functions of a complex variable).Liouville's theorem
If f is a harmonic function defined on all of Rn which is bounded above or bounded below, then f is constant (compare Liouville's theorem for functions of a complex variableLiouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
).
Edward Nelson
Edward Nelson
Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...
gave a particularly short proof of this theorem, using the mean value property mentioned above:
Given two points, choose
two balls with the given points as centers and of equal radius. If the
radius is large enough, the two balls will coincide except for an
arbitrarily small proportion of their volume. Since f is
bounded, the averages of it over the two balls are arbitrarily close,
and so f assumes the same value at any two points.
Weakly harmonic function
A function (or, more generally, a distributionDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
) is weakly harmonic
Weakly harmonic
In mathematics, a function f is weakly harmonic in a domain D if\int_D f\, \Delta g = 0for all g with compact support in D and continuous second derivatives, where Δ is the Laplacian. This is the same notion as a weak derivative, however, a function can have a weak derivative and not be...
if it satisfies Laplace's equation
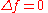
in a weak
Weak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
sense (or, equivalently, in the sense of distributions). A weakly harmonic function coincides almost everywhere with a strongly harmonic function, and is in particular smooth. A weakly harmonic distribution is precisely the distribution associated to a strongly harmonic function, and so also is smooth. This is Weyl's lemma
Weyl's lemma (Laplace equation)
In mathematics, Weyl's lemma is a result that provides a "very weak" form of the Laplace equation. It is named after the German mathematician Hermann Weyl.-Statement of the lemma:...
.
There are other weak formulation
Weak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
s of Laplace's equation that are often useful. One of which is Dirichlet's principle, representing harmonic functions in the Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
H1(Ω) as the minimizers of the Dirichlet energy
Dirichlet energy
In mathematics, the Dirichlet's energy is a numerical measure of how variable a function is. More abstractly, it is a quadratic functional on the Sobolev space...
integral
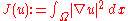
with respect to local variations, that is, all functions
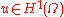 such that
such that 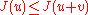 holds for all
holds for all 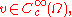 or equivalently, for all
or equivalently, for all 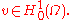
Harmonic functions on manifolds
Harmonic functions can be defined on an arbitrary Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, using the Laplace-Beltrami operator
Laplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
Δ. In this context, a function is called harmonic if
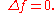
Many of the properties of harmonic functions on domains in Euclidean space carry over to this more general setting, including the mean value theorem (over geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
balls), the maximum principle, and the Harnack inequality. With the exception of the mean value theorem, these are easy consequences of the corresponding results for general linear elliptic partial differential equations of the second order.
Subharmonic functions
A C2 function that satisfies is called subharmonic. This condition guarantees that the maximum principle will hold, although other properties of harmonic functions may fail. More generally, a function is subharmonic if and only if, in the interior of any ball in its domain, its graph lies below that of the harmonic function interpolating its boundary values on the ball.
is called subharmonic. This condition guarantees that the maximum principle will hold, although other properties of harmonic functions may fail. More generally, a function is subharmonic if and only if, in the interior of any ball in its domain, its graph lies below that of the harmonic function interpolating its boundary values on the ball.Harmonic forms
One generalization of the study of harmonic functions is the study of harmonic forms on Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s, and it is related to the study of cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
. Also, it is possible to define harmonic vector-valued functions, or harmonic maps of two Riemannian manifolds, which are critical points of a generalized Dirichlet energy functional (this includes harmonic functions as a special case, a result known as Dirichlet principle). These kind of harmonic maps appear in the theory of minimal surfaces. For example, a curve, that is, a map from an interval in R to a Riemannian manifold, is a harmonic map if and only if it is a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
.
Harmonic maps between manifolds
If M and N are two Riemannian manifolds, then a harmonic map is defined to be a stationary point of the Dirichlet energy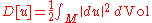
in which is the differential of u, and the norm is that induced by the metric on M and that on N on the tensor product bundle T∗M⊗u−1TN.
Important special cases of harmonic maps between manifolds include minimal surface
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
s, which are precisely the harmonic immersions of a surface into three-dimensional Euclidean space. More generally, minimal submanifolds are harmonic immersions of one manifold in another. Harmonic coordinates
Harmonic coordinates
In Riemannian geometry, a branch of mathematics, harmonic coordinates are a coordinate system on a Riemannian manifold each of whose coordinate functions xi is harmonic, meaning that it satisfies Laplace's equation\Delta x^i = 0.\,...
are a harmonic diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
from a manifold to an open subset of a Euclidean space of the same dimension.
See also
- Dirichlet problemDirichlet problemIn mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
- Dirichlet principle
- Dirichlet energyDirichlet energyIn mathematics, the Dirichlet's energy is a numerical measure of how variable a function is. More abstractly, it is a quadratic functional on the Sobolev space...
- Heat equationHeat equationThe heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
- Laplace's equationLaplace's equationIn mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
- Poisson's equationPoisson's equationIn mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
- Quadrature domainsQuadrature domainsIn the branch of mathematics called potential theory, a quadrature domain in two dimensional real Euclidean space is a domain D together with...
- Subharmonic functionSubharmonic functionIn mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
- Harmonic map