
Quadrature domains
Encyclopedia
In the branch of mathematics
called potential theory
, a quadrature domain in two dimensional real Euclidean space is a domain D (an open
connected set
) together with
a finite subset {z1, …, zk} of D such that, for every function u harmonic
and integrable over D with respect to area measure, the integral of u with respect to this measure is given by a "quadrature formula"; that is,
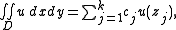
where the cj are nonzero complex constants independent of u.
The most obvious example is when D is a circular disk: here k = 1, z1 is the center of the circle, and c1 equals the area of D. That quadrature formula expresses the mean value property of harmonic functions with respect to disks.
It is known that quadrature domains exist for all values of k. There is an analogous definition of quadrature domains in Euclidean space of dimension d larger than 2. There is also an alternative, electrostatic interpretation of quadrature domains: a domain D is a quadrature domain if a uniform distribution of electric charge on D creates the same electrostatic field outside D as does a k-tuple of point charges at the points z1, …, zk.
Quadrature domains and numerous generalizations thereof (e.g., replace area measure by length measure on the boundary of D) have in recent years been encountered in various connections such as inverse problems of Newtonian gravitation
, Hele-Shaw flow
s of viscous fluids, and purely mathematical isoperimetric problems, and interest in them seems to be steadily growing. They were the subject of an international conference at the University of California at Santa Barbara in 2003 and the state of the art as of that date can be seen in the proceedings of that conference, published by Birkhäuser Verlag.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
called potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
, a quadrature domain in two dimensional real Euclidean space is a domain D (an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
connected set
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
) together with
a finite subset {z1, …, zk} of D such that, for every function u harmonic
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
and integrable over D with respect to area measure, the integral of u with respect to this measure is given by a "quadrature formula"; that is,
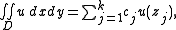
where the cj are nonzero complex constants independent of u.
The most obvious example is when D is a circular disk: here k = 1, z1 is the center of the circle, and c1 equals the area of D. That quadrature formula expresses the mean value property of harmonic functions with respect to disks.
It is known that quadrature domains exist for all values of k. There is an analogous definition of quadrature domains in Euclidean space of dimension d larger than 2. There is also an alternative, electrostatic interpretation of quadrature domains: a domain D is a quadrature domain if a uniform distribution of electric charge on D creates the same electrostatic field outside D as does a k-tuple of point charges at the points z1, …, zk.
Quadrature domains and numerous generalizations thereof (e.g., replace area measure by length measure on the boundary of D) have in recent years been encountered in various connections such as inverse problems of Newtonian gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, Hele-Shaw flow
Hele-Shaw flow
Hele-Shaw flow is defined as Stokes Flow between two parallel flat plates separated by an infinitesimally small gap. Various problems in fluid mechanics can be approximated to Hele-Shaw flows and thus the research of these flows is of importance. Approximation to Hele-Shaw flow is specifically...
s of viscous fluids, and purely mathematical isoperimetric problems, and interest in them seems to be steadily growing. They were the subject of an international conference at the University of California at Santa Barbara in 2003 and the state of the art as of that date can be seen in the proceedings of that conference, published by Birkhäuser Verlag.

