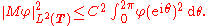Subharmonic function
Encyclopedia
In mathematics
, subharmonic and superharmonic functions are important classes of functions
used extensively in partial differential equations, complex analysis
and potential theory
.
Intuitively, subharmonic functions are related to convex function
s of one variable as follows. If the graph
of a convex function and a line intersect at two points, then the graph of the convex function is below the line between those points. In the same way, if the values of a subharmonic function are no larger than the values of a harmonic function
on the boundary of a ball
, then the values of the subharmonic function are no larger than the values of the harmonic function also inside the ball.
Superharmonic functions can be defined by the same description, only replacing "no larger" with "no smaller". Alternatively, a superharmonic function is just the negative
of a subharmonic function, and for this reason any property of subharmonic functions can be easily transferred to superharmonic functions.
 be a subset of the Euclidean space
be a subset of the Euclidean space
 and let
and let
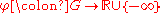
be an upper semi-continuous function
. Then,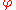 is called subharmonic if for any closed ball
is called subharmonic if for any closed ball  of center
of center  and radius
and radius  contained in
contained in  and every real
and every real
-valued continuous function
 on
on  that is harmonic in
that is harmonic in 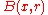 and satisfies
and satisfies  for all
for all  on the boundary
on the boundary
 of
of  we have
we have  for all
for all 
Note that by the above, the function which is identically −∞ is subharmonic, but some authors exclude this function by definition.
, where they are intimately connected to holomorphic function
s.
One can show that a real-valued, continuous function of a complex variable (that is, of two real variables) defined on a set
of a complex variable (that is, of two real variables) defined on a set  is subharmonic if and only if for any closed disc
is subharmonic if and only if for any closed disc 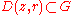 of center
of center  and radius
and radius  one has
one has

Intuitively, this means that a subharmonic function is at any point no greater than the average
of the values in a circle around that point, a fact which can be used to derive the maximum principle
.
If is a holomorphic function, then
is a holomorphic function, then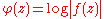
is a subharmonic function if we define the value of at the zeros of
at the zeros of  to be −∞. It follows that
to be −∞. It follows that
is subharmonic for every α > 0. This observation plays a role in the theory of Hardy spaces, especially for the study of Hp when 0 < p < 1.
In the context of the complex plane, the connection to the convex function
s can be realized as well by the fact that a subharmonic function on a domain
on a domain  that is constant in the imaginary direction is convex in the real direction and vice versa.
that is constant in the imaginary direction is convex in the real direction and vice versa.
 is subharmonic in a region
is subharmonic in a region
 of the complex plane, and
of the complex plane, and 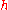 is harmonic
is harmonic
on , then
, then 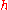 is a harmonic majorant of
is a harmonic majorant of  in
in  if
if  ≤
≤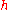 in
in  . Such an inequality can be viewed as a growth condition on
. Such an inequality can be viewed as a growth condition on  .
.
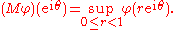
If Pr denotes the Poisson kernel
, it follows from the subharmonicity that
It can be shown that the last integral is less than the value at e iθ of the Hardy–Littlewood maximal function φ∗ of the restriction of φ to the unit circle T,
so that 0 ≤ M φ ≤ φ∗. It is known that the Hardy–Littlewood operator is bounded on Lp(T)
when 1 < p < ∞.
It follows that for some universal constant C,
If f is a function holomorphic in Ω and 0 < p < ∞, then the preceding inequality applies to φ = |f | p/2. It can be deduced from these facts that any function F in the classical Hardy space Hp satisfies
With more work, it can be shown that F has radial limits F(e iθ) almost everywhere on the unit circle, and (by the dominated convergence theorem
) that Fr, defined by Fr(e iθ) = F(r e iθ) tends to F in Lp(T).
.
Definition: Let M be a Riemannian manifold, and an upper semicontinuous function. Assume that for any open subset
an upper semicontinuous function. Assume that for any open subset  , and any harmonic function
, and any harmonic function
f1 on U, such that on the boundary of U, the inequality
on the boundary of U, the inequality  holds on all U. Then f is called subharmonic.
holds on all U. Then f is called subharmonic.
This definition is equivalent to one given above. Also, for twice differentiable functions, subharmonicity is equivalent to the inequality , where
, where  is the usual Laplacian
is the usual Laplacian
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, subharmonic and superharmonic functions are important classes of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
used extensively in partial differential equations, complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
and potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
.
Intuitively, subharmonic functions are related to convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
s of one variable as follows. If the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of a convex function and a line intersect at two points, then the graph of the convex function is below the line between those points. In the same way, if the values of a subharmonic function are no larger than the values of a harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
on the boundary of a ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
, then the values of the subharmonic function are no larger than the values of the harmonic function also inside the ball.
Superharmonic functions can be defined by the same description, only replacing "no larger" with "no smaller". Alternatively, a superharmonic function is just the negative
Additive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of a subharmonic function, and for this reason any property of subharmonic functions can be easily transferred to superharmonic functions.
Formal definition
Formally, the definition can be stated as follows. Let be a subset of the Euclidean space
be a subset of the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
 and let
and let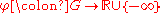
be an upper semi-continuous function
Semi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
. Then,
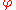 is called subharmonic if for any closed ball
is called subharmonic if for any closed ball  of center
of center  and radius
and radius  contained in
contained in  and every real
and every realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
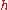 on
on  that is harmonic in
that is harmonic in 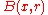 and satisfies
and satisfies  for all
for all  on the boundary
on the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
 of
of  we have
we have  for all
for all 
Note that by the above, the function which is identically −∞ is subharmonic, but some authors exclude this function by definition.
Properties
- A function is harmonicHarmonic functionIn mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is both subharmonic and superharmonic. - If
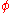 is C2 (twice continuously differentiableSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
is C2 (twice continuously differentiableSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
) on an open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
 in
in  , then
, then 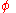 is subharmonic if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
is subharmonic if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
one has on
on 
- where
 is the Laplacian.
is the Laplacian.
- The maximumMaxima and minimaIn mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of a subharmonic function cannot be achieved in the interiorInterior (topology)In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of its domain unless the function is constant, this is the so-called maximum principleMaximum principleIn mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
. - Subharmonic functions are upper semicontinuous, while superharmonic functions are lower semicontinuous.
- The maximum
Subharmonic functions in the complex plane
Subharmonic functions are of a particular importance in complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, where they are intimately connected to holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s.
One can show that a real-valued, continuous function
 of a complex variable (that is, of two real variables) defined on a set
of a complex variable (that is, of two real variables) defined on a set  is subharmonic if and only if for any closed disc
is subharmonic if and only if for any closed disc 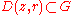 of center
of center  and radius
and radius  one has
one has
Intuitively, this means that a subharmonic function is at any point no greater than the average
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of the values in a circle around that point, a fact which can be used to derive the maximum principle
Maximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
.
If
 is a holomorphic function, then
is a holomorphic function, then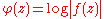
is a subharmonic function if we define the value of
 at the zeros of
at the zeros of  to be −∞. It follows that
to be −∞. It follows that
is subharmonic for every α > 0. This observation plays a role in the theory of Hardy spaces, especially for the study of Hp when 0 < p < 1.
In the context of the complex plane, the connection to the convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
s can be realized as well by the fact that a subharmonic function
 on a domain
on a domain  that is constant in the imaginary direction is convex in the real direction and vice versa.
that is constant in the imaginary direction is convex in the real direction and vice versa.Harmonic majorants of subharmonic functions
If is subharmonic in a region
is subharmonic in a regionRegion (mathematical analysis)
In mathematical analysis, the word region usually refers to a subset of \R^n that is open , connected and non-empty. A closed region is sometimes defined to be the closure of a region....
 of the complex plane, and
of the complex plane, and 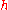 is harmonic
is harmonicHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
on
 , then
, then 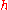 is a harmonic majorant of
is a harmonic majorant of  in
in  if
if  ≤
≤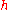 in
in  . Such an inequality can be viewed as a growth condition on
. Such an inequality can be viewed as a growth condition on  .
.Subharmonic functions in the unit disc. Radial maximal function
Let φ be subharmonic, continuous and non-negative in an open subset Ω of the complex plane containing the closed unit disc D(0, 1). The radial maximal function for the function φ (restricted to the unit disc) is defined on the unit circle by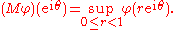
If Pr denotes the Poisson kernel
Poisson kernel
In potential theory, the Poisson kernel is an integral kernel, used for solving the two-dimensional Laplace equation, given Dirichlet boundary conditions on the unit disc. The kernel can be understood as the derivative of the Green's function for the Laplace equation...
, it follows from the subharmonicity that

It can be shown that the last integral is less than the value at e iθ of the Hardy–Littlewood maximal function φ∗ of the restriction of φ to the unit circle T,

so that 0 ≤ M φ ≤ φ∗. It is known that the Hardy–Littlewood operator is bounded on Lp(T)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
when 1 < p < ∞.
It follows that for some universal constant C,
If f is a function holomorphic in Ω and 0 < p < ∞, then the preceding inequality applies to φ = |f | p/2. It can be deduced from these facts that any function F in the classical Hardy space Hp satisfies
With more work, it can be shown that F has radial limits F(e iθ) almost everywhere on the unit circle, and (by the dominated convergence theorem
Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
) that Fr, defined by Fr(e iθ) = F(r e iθ) tends to F in Lp(T).
Subharmonic functions on Riemannian manifolds
Subharmonic functions can be defined on an arbitrary Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
.
Definition: Let M be a Riemannian manifold, and
 an upper semicontinuous function. Assume that for any open subset
an upper semicontinuous function. Assume that for any open subset  , and any harmonic function
, and any harmonic functionHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
f1 on U, such that
 on the boundary of U, the inequality
on the boundary of U, the inequality  holds on all U. Then f is called subharmonic.
holds on all U. Then f is called subharmonic.This definition is equivalent to one given above. Also, for twice differentiable functions, subharmonicity is equivalent to the inequality
 , where
, where  is the usual Laplacian
is the usual LaplacianLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
.
See also
- Plurisubharmonic functionPlurisubharmonic functionIn mathematics, plurisubharmonic functions form an important class of functions used in complex analysis. On a Kähler manifold, plurisubharmonic functions form a subset of the subharmonic functions...
— generalization to several complex variablesSeveral complex variablesThe theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers... - Classical fine topology