Dominated convergence theorem - AbsoluteAstronomy.com

In measure theory, Lebesgue

Henri Lebesgue

Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...

's dominated convergence theorem provides sufficient conditions under which two limit processes

Limit (mathematics)

In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...

commute, namely Lebesgue integration and almost everywhere

Almost everywhere

In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...

convergence

Convergence

-Mathematics:* Convergence , refers to the notion that some functions and sequences approach a limit under certain conditions* Convergence , the notion that a sequence of transformations come to the same conclusion, no matter what order they are performed in.-Natural sciences:*Convergence ,...

of a sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

of functions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

. The dominated convergence theorem does not hold for the Riemann integral

Riemann integral

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...

because the limit of a sequence of Riemann-integrable functions is in many cases not Riemann-integrable. Its power and utility are two of the primary theoretical advantages of Lebesgue integration over Riemann integration.

It is widely used in probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, since it gives a sufficient condition for the convergence of expected value

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

s of random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

Statement of the theorem

Let {ƒ_n} denote a sequence of real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

-valued measurable function

Measurable function

In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

s on a measure space . Assume that the sequence converges pointwise to a function ƒ and is dominated by some integrable function g in the sense that

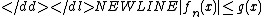
for all numbers n in the index set of the sequence and all points x in S.
Then the limiting function ƒ is integrable and

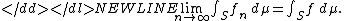
(By integrable we mean

)

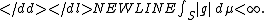Remarks:

The convergence of the sequence and domination by g can be relaxed to hold only almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...

provided the measure space is complete or ƒ is chosen as a measurable function which agrees everywhere with the everywhere existing pointwise limit. (These precautions are necessary, because otherwise there might exist a non-measurable subset
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....

of a set , hence ƒ might not be measurable.)
The condition that there is a dominating integrable function g can be relaxed to uniform integrability of the sequence {ƒ_n}, see Vitali convergence theorem
Vitali convergence theorem
In mathematics, the Vitali convergence theorem is a generalization of the better-known dominated convergence theorem of Henri Lebesgue. It is useful when a dominating function cannot be found for the sequence of functions in question; when such a dominating function can be found, Lebesgue's theorem...

.

Proof of the theorem

Lebesgue's dominated convergence theorem is a special case of the Fatou–Lebesgue theorem

Fatou–Lebesgue theorem

In mathematics, the Fatou–Lebesgue theorem establishes a chain of inequalities relating the integrals of the limit inferior and the limit superior of a sequence of functions to the limit inferior and the limit superior of integrals of these functions...

. Below is a direct proof, using Fatou’s lemma as the essential tool.

As the pointwise limit of the sequence, ƒ is also measurable and dominated by g, hence integrable. Furthermore,

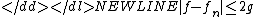
for all n and

By the reverse Fatou lemma,

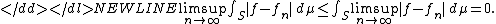
Using linearity and monotonicity of the Lebesgue integral,

and the theorem follows.

If the assumptions hold only everywhere, then there exists a set such that the functions ƒ_n1N satisfy the assumptions everywhere on S. Then ƒ(x) is the pointwise limit of ƒ_n(x) for and for , hence ƒ is measurable. The values of the integrals are not influenced by this μ-null set N.

Discussion of the assumptions
The assumption that the sequence is dominated by some integrable g can not be dispensed with. This may be seen as follows: define for x in the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

and otherwise. Any g which dominates the sequence must also dominate the pointwise supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

. Observe that

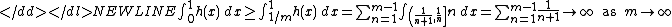
by the divergence of the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...

. Hence, the monotonicity of the Lebesgue integral tells us that there exists no integrable function which dominates the sequence on [0,1]. A direct calculation shows that integration and pointwise limit do not commute for this sequence:

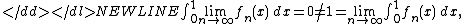
because the pointwise limit of the sequence is the zero function. Note that the sequence {ƒ_n} is not even uniformly integrable, hence also the Vitali convergence theorem
Vitali convergence theorem
In mathematics, the Vitali convergence theorem is a generalization of the better-known dominated convergence theorem of Henri Lebesgue. It is useful when a dominating function cannot be found for the sequence of functions in question; when such a dominating function can be found, Lebesgue's theorem...

is not applicable.

Bounded convergence theorem
One corollary to the dominated convergence theorem is the bounded convergence theorem, which states that if ƒ₁, ƒ₂, ƒ₃, … is a sequence of uniformly bounded
Uniform boundedness
In mathematics, bounded functions are functions for which there exists a lower bound and an upper bound, in other words, a constant which is larger than the absolute value of any value of this function. If we consider a family of bounded functions, this constant can vary between functions...

real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

-valued measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

s which converges pointwise on a bounded measure space (i.e. one in which μ(S) is finite) to a function ƒ, then the limit ƒ is an integrable function and

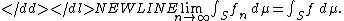
Remark: The pointwise convergence and uniform boundedness of the sequence can be relaxed to hold only almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...

, provided the measure space is complete or ƒ is chosen as a measurable function which agrees μ-almost everywhere with the everywhere existing pointwise limit.

Proof
Since the sequence is uniformly bounded, there is a real number M such that for all and for all n. Define for all . Then the sequence is dominated by g. Furthermore, g is integrable since it is a constant function on a set of finite measure. Therefore the result follows from the dominated convergence theorem.

If the assumptions hold only everywhere, then there exists a set such that the functions ƒ_n1_N satisfy the assumptions everywhere on S.

Extensions
The dominated convergence theorem applies also to measurable functions with values in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

, with the dominating function still being non-negative and integrable as above.

See also

Convergence of random variables
Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...

, Convergence in mean

Monotone convergence theorem (does not require domination by an integrable function but assumes monotonicity of the sequence instead)

Scheffé’s lemma

Uniform integrability

Vitali convergence theorem
Vitali convergence theorem
In mathematics, the Vitali convergence theorem is a generalization of the better-known dominated convergence theorem of Henri Lebesgue. It is useful when a dominating function cannot be found for the sequence of functions in question; when such a dominating function can be found, Lebesgue's theorem...

(a generalization of Lebesgue's dominated convergence theorem)

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.