
Uniform boundedness
Encyclopedia
In mathematics
, bounded function
s are functions
for which there exists a lower bound and an upper bound
, in other words, a constant which is larger than the absolute value
of any value of this function. If we consider a family of bounded functions, this constant can vary between functions. If it is possible to find one constant which bounds all functions, this family of functions is uniformly bounded.
The uniform boundedness principle
in functional analysis
provides sufficient conditions for uniform boundedness of a family of operators.
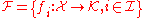
be a family of functions indexed
by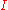 , where
, where  is an arbitrary set and
is an arbitrary set and  is the set of real
is the set of real
or complex
numbers. We call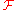 uniformly bounded if there exists a real number
uniformly bounded if there exists a real number  such that
such that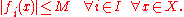
 be a metric space
be a metric space
with metric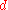 , then the set
, then the set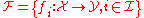
is called uniformly bounded if there exists an element from
from  and a real number
and a real number  such that
such that
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, bounded function
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
s are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
for which there exists a lower bound and an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
, in other words, a constant which is larger than the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of any value of this function. If we consider a family of bounded functions, this constant can vary between functions. If it is possible to find one constant which bounds all functions, this family of functions is uniformly bounded.
The uniform boundedness principle
Uniform boundedness principle
In mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field...
in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
provides sufficient conditions for uniform boundedness of a family of operators.
Real line and complex plane
Let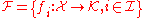
be a family of functions indexed
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
by
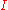 , where
, where  is an arbitrary set and
is an arbitrary set and  is the set of real
is the set of realReal
Real may also refer to:* Reality, the state of things as they actually exist, rather than as they may appear or may be thought to be.-Finance:* Inflation adjusted amountsCurrencies:* Brazilian realFormer currencies:* Mexican real* Portuguese real...
or complex
Complex
A complex is a whole that comprehends a number of intricate parts, especially one with interconnected or mutually related parts; for example, a complex of buildings.Complex may refer to:-Biology:...
numbers. We call
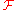 uniformly bounded if there exists a real number
uniformly bounded if there exists a real number  such that
such that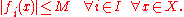
Metric space
In general let be a metric space
be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
with metric
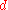 , then the set
, then the set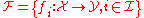
is called uniformly bounded if there exists an element
 from
from  and a real number
and a real number  such that
such that
Examples
- Every uniformly convergent sequence of bounded functions is uniformly bounded.
- The family of functions
 defined for realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
defined for realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
 with
with  traveling through the integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
traveling through the integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, is uniformly bounded by 1.
- The family of derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of the above family, is not uniformly bounded. Each
is not uniformly bounded. Each  is bounded by
is bounded by  but there is no real number
but there is no real number  such that
such that  for all integers
for all integers 

