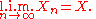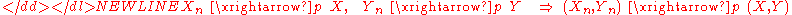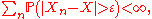Convergence of random variables
Encyclopedia
In probability theory
, there exist several different notions of convergence of random variables. The convergence
of sequence
s of random variable
s to some limit
random variable is an important concept in probability theory, and its applications to statistics
and stochastic process
es. The same concepts are known in more general mathematics
as stochastic convergence and they formalize the idea that a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behaviour that is essentially unchanging when items far enough into the sequence are studied. The different possible notions of convergence relate to how such a behaviour can be characterised: two readily understood behaviours are that the sequence eventually takes a constant value, and that values in the sequence continue to change but can be described by an unchanging probability distribution.
Some less obvious, more theoretical patterns could be
These other types of patterns that may arise are reflected in the different types of stochastic convergence that have been studied.
While the above discussion has related to the convergence of a single series to a limiting value, the notion of the convergence of two series towards each other is also important, but this is easily handled by studying the sequence defined as either the difference or the ratio of the two series.
For example, if the average of n uncorrelated
random variables Yi, i = 1, ..., n, all having the same finite mean
and variance
, is given by
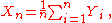
then as n tends to infinity, Xn converges in probability (see below) to the common mean
, μ, of the random variables Yi. This result is known as the weak law of large numbers. Other forms of convergence are important in other useful theorems, including the central limit theorem
.
Throughout the following, we assume that (Xn) is a sequence of random variables, and X is a random variable, and all of them are defined on the same probability space
 .
.
, the distribution of Zn approaches the normal N(0, ⅓) distribution. This convergence is shown in the picture: as n grows larger, the shape of the pdf function gets closer and closer to the Gaussian curve.
}}
With this mode of convergence, we increasingly expect to see the next outcome in a sequence of random experiments becoming better and better modeled by a given probability distribution
.
Convergence in distribution is the weakest form of convergence, since it is implied by all other types of convergence mentioned in this article. However convergence in distribution is very frequently used in practice; most often it arises from application of the central limit theorem
.
s is said to converge in distribution, or converge weakly, or converge in law to a random variable X if
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, there exist several different notions of convergence of random variables. The convergence
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s to some limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
random variable is an important concept in probability theory, and its applications to statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es. The same concepts are known in more general mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
as stochastic convergence and they formalize the idea that a sequence of essentially random or unpredictable events can sometimes be expected to settle down into a behaviour that is essentially unchanging when items far enough into the sequence are studied. The different possible notions of convergence relate to how such a behaviour can be characterised: two readily understood behaviours are that the sequence eventually takes a constant value, and that values in the sequence continue to change but can be described by an unchanging probability distribution.
Background
"Stochastic convergence" formalizes the idea that a sequence of essentially random or unpredictable events can sometimes be expected to settle into a pattern. The pattern may for instance be- ConvergenceLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
in the classical sense to a fixed value, perhaps itself coming from a random event - An increasing similarity of outcomes to what a purely deterministic function would produce
- An increasing preference towards a certain outcome
- An increasing "aversion" against straying far away from a certain outcome
Some less obvious, more theoretical patterns could be
- That the probability distribution describing the next outcome may grow increasingly similar to a certain distribution
- That the series formed by calculating the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the outcome's distance from a particular value may converge to 0 - That the variance of the random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
describing the next event grows smaller and smaller.
These other types of patterns that may arise are reflected in the different types of stochastic convergence that have been studied.
While the above discussion has related to the convergence of a single series to a limiting value, the notion of the convergence of two series towards each other is also important, but this is easily handled by studying the sequence defined as either the difference or the ratio of the two series.
For example, if the average of n uncorrelated
Uncorrelated
In probability theory and statistics, two real-valued random variables are said to be uncorrelated if their covariance is zero. Uncorrelatedness is by definition pairwise; i.e...
random variables Yi, i = 1, ..., n, all having the same finite mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, is given by
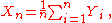
then as n tends to infinity, Xn converges in probability (see below) to the common mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
, μ, of the random variables Yi. This result is known as the weak law of large numbers. Other forms of convergence are important in other useful theorems, including the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
.
Throughout the following, we assume that (Xn) is a sequence of random variables, and X is a random variable, and all of them are defined on the same probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
 .
.Convergence in distribution
}\sum_{i=1}^n X_i be their (normalized) sums. Then according to the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, the distribution of Zn approaches the normal N(0, ⅓) distribution. This convergence is shown in the picture: as n grows larger, the shape of the pdf function gets closer and closer to the Gaussian curve.
}}
With this mode of convergence, we increasingly expect to see the next outcome in a sequence of random experiments becoming better and better modeled by a given probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
.
Convergence in distribution is the weakest form of convergence, since it is implied by all other types of convergence mentioned in this article. However convergence in distribution is very frequently used in practice; most often it arises from application of the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
.
Definition
A sequence {X1, X2, …} of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s is said to converge in distribution, or converge weakly, or converge in law to a random variable X if
-

for every number at which F is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Here Fn and F are the cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s of random variables Xn and X correspondingly.
The requirement that only the continuity points of F should be considered is essential. For example if Xn are distributed uniformlyUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on intervals [0, ], then this sequence converges in distribution to a degenerate random variable . Indeed, for all n when , and for all when . However, for this limiting random variable , even though for all n. Thus the convergence of cdfs fails at the point where F is discontinuous.
Convergence in distribution may be denoted as-

where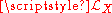 is the law (probability distribution) of X. For example if X is standard normal we can write .
is the law (probability distribution) of X. For example if X is standard normal we can write .
For random vectors {X1, X2, …} ⊂ Rk the convergence in distribution is defined similarly. We say that this sequence converges in distribution to a random k-vector X if-
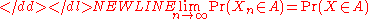
for every A ⊂ Rk which is a continuity setContinuity setIn measure theory, a continuity set of a measure μ is any Borel set B such that |\mu| = 0\,. The class of all continuity sets for given measure μ forms a ring....
of X.
The definition of convergence in distribution may be extended from random vectors to more complex random elementRandom elementIn probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...
s in arbitrary metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, and even to the “random variables” which are not measurable — a situation which occurs for example in the study of empirical processEmpirical processThe study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...
es. This is the “weak convergence of laws without laws being defined” — except asymptotically.
In this case the term weak convergence is preferable (see weak convergence of measures), and we say that a sequence of random elements {Xn} converges weakly to X (denoted as Xn ⇒ X) if-

for all continuous bounded functions h(·). Here E* denotes the outer expectation, that is the expectation of a “smallest measurable function g that dominates h(Xn)”.
Properties
- Since F(a) = Pr(X ≤ a), the convergence in distribution means that the probability for Xn to be in a given range is approximately equal to the probability that the value of X is in that range, provided n is sufficiently large.
- In general, convergence in distribution does not imply that the sequence of corresponding probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s will also converge. As an example one may consider random variables with densities ƒn(x) = (1 − cos(2πnx))1{x∈(0,1)}. These random variables converge in distribution to a uniform U(0, 1), whereas their densities do not converge at all.
- Portmanteau lemma provides several equivalent definitions of convergence in distribution. Although these definitions are less intuitive, they are used to prove a number of statistical theorems. The lemma states that {Xn} converges in distribution to X if and only if any of the following statements are true:
- Eƒ(Xn) → Eƒ(X) for all boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
, continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s ƒ; - Eƒ(Xn) → Eƒ(X) for all bounded, Lipschitz functions ƒ;
- limsup{ Eƒ(Xn) } ≤ Eƒ(X) for every upper semi-continuous function ƒ bounded from above;
- liminf{ Eƒ(Xn) } ≥ Eƒ(X) for every lower semi-continuous function ƒ bounded from below;
- limsup{ Pr(Xn ∈ C) } ≤ Pr(X ∈ C) for all closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s C; - liminf{ Pr(Xn ∈ U) } ≥ Pr(X ∈ U) for all open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s U; - lim{ Pr(Xn ∈ A) } = Pr(X ∈ A) for all continuity setContinuity setIn measure theory, a continuity set of a measure μ is any Borel set B such that |\mu| = 0\,. The class of all continuity sets for given measure μ forms a ring....
s A of random variable X.
- Eƒ(Xn) → Eƒ(X) for all bounded
- Continuous mapping theoremContinuous mapping theoremIn probability theory, the continuous mapping theorem states that continuous functions are limit-preserving even if their arguments are sequences of random variables. A continuous function, in Heine’s definition, is such a function that maps convergent sequences into convergent sequences: if xn → x...
states that for a continuous function g(·), if the sequence {Xn} converges in distribution to X, then so does {g(Xn)} converge in distribution to g(X).
- Lévy’s continuity theorem: the sequence {Xn} converges in distribution to X if and only if the sequence of corresponding characteristic functionCharacteristic function (probability theory)In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
s {φn} converges pointwisePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
to the characteristic function φ of X, and φ(t) is continuous at t = 0.
- Convergence in distribution is metrizable by the Lévy–Prokhorov metric.
- A natural link to convergence in distribution is the Skorokhod's representation theoremSkorokhod's representation theoremIn mathematics and statistics, Skorokhod's representation theorem is a result that shows that a weakly convergent sequence of probability measures whose limit measure is sufficiently well-behaved can be represented as the distribution/law of a pointwise convergent sequence of random variables...
.
Convergence in probability
The basic idea behind this type of convergence is that the probability of an “unusual” outcome becomes smaller and smaller as the sequence progresses.
The concept of convergence in probability is used very often in statistics. For example, an estimator is called consistentConsistent estimatorIn statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
if it converges in probability to the quantity being estimated. Convergence in probability is also the type of convergence established by the weak law of large numbers.
Definition
A sequence {Xn} of random variables converges in probability towards X if for all ε > 0-

Formally, pick any ε > 0 and any δ > 0. Let Pn be the probability that Xn is outside the ball of radius ε centered at X. Then for Xn to converge in probability to X there should exist a number Nδ such that for all n ≥ Nδ the probability Pn is less than δ.
Convergence in probability is denoted by adding the letter p over an arrow indicating convergence, or using the “plim” probability limit operator:-
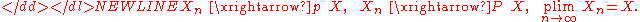
For random elements {Xn} on a separable metric space (S, d), convergence in probability is defined similarly by-
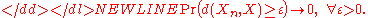
Properties
- Convergence in probability implies convergence in distribution.[proof]
- Convergence in probability implies almost sure convergence on discrete probability spaces. Since A.S. convergence always implies convergence in probability, in the discrete case, strong convergence and convergence in probability mean the same thing.[proof]
- In the opposite direction, convergence in distribution implies convergence in probability only when the limiting random variable X is a constant.[proof]
- The continuous mapping theoremContinuous mapping theoremIn probability theory, the continuous mapping theorem states that continuous functions are limit-preserving even if their arguments are sequences of random variables. A continuous function, in Heine’s definition, is such a function that maps convergent sequences into convergent sequences: if xn → x...
states that for every continuous function g(·), if , then also .
- Convergence in probability defines a topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on the space of random variables over a fixed probability space. This topology is metrizable by the Ky Fan metric:
d(X,Y) = \inf\!\big\{ \varepsilon>0:\ \Pr\big(|X-Y|>\varepsilon\big)\leq\varepsilon\big\}.
Almost sure convergence
This is the type of stochastic convergence that is most similar to pointwise convergencePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
known from elementary real analysisReal analysisReal analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
.
Definition
To say that the sequence Xn converges almost surely or almost everywhere or with probability 1 or strongly towards X means that-

This means that the values of Xn approach the value of X, in the sense (see almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
) that events for which Xn does not converge to X have probability 0. Using the probability space and the concept of the random variable as a function from Ω to R, this is equivalent to the statement
and the concept of the random variable as a function from Ω to R, this is equivalent to the statement
-

Another, equivalent, way of defining almost sure convergence is as follows:-

Almost sure convergence is often denoted by adding the letters a.s. over an arrow indicating convergence:-
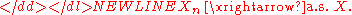
For generic random elementRandom elementIn probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line...
s {Xn} on a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(S, d), convergence almost surely is defined similarly:-

Properties
- Almost sure convergence implies convergence in probability, and hence implies convergence in distribution. It is the notion of convergence used in the strong law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
. - The concept of almost sure convergence does not come from a topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. This means there is no topology on the space of random variables such that the almost surely convergent sequences are exactly the converging sequences with respect to that topology. In particular, there is no metric of almost sure convergence.
Sure convergence
To say that the sequence or random variables (Xn) defined over the same probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(i.e., a random process) converges surely or everywhere or pointwise towards X means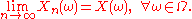
where Ω is the sample space of the underlying probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
over which the random variables are defined.
This is the notion of pointwise convergencePointwise convergenceIn mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
of sequence functions extended to sequence of random variables. (Note that random variables themselves are functions).

Sure convergence of a random variable implies all the other kinds of convergence stated above, but there is no payoff in probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
by using sure convergence compared to using almost sure convergence. The difference between the two only exists on sets with probability zero. This is why the concept of sure convergence of random variables is very rarely used.
Convergence in mean
We say that the sequence Xn converges in the r-th mean (or in the Lr-normLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
) towards X, for some , if absolute momentMoment- Science, engineering, and mathematics :* Moment , used in probability theory and statistics* Moment , several related concepts, including:** Angular momentum or moment of momentum, the rotational analog of momentum...
s of Xn and X exist, and-

where the operator E denotes the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. Convergence in mean tells us that the expectation of the power of the difference between Xn and X converges to zero.
This type of convergence is often denoted by adding the letter Lr over an arrow indicating convergence:
The most important cases of convergence in r-th mean are:- When Xn converges in r-th mean to X for r = 1, we say that Xn converges in mean to X.
- When Xn converges in r-th mean to X for r = 2, we say that Xn converges in mean square to X. This is also sometimes referred to as convergence in mean, and is sometimes denoted
Convergence in the r-th mean, for r > 0, implies convergence in probability (by Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
), while if r > s ≥ 1, convergence in r-th mean implies convergence in s-th mean. Hence, convergence in mean square implies convergence in mean.
Convergence in rth-order mean
Examples of convergence in rth-order mean.
Basic example:
A newly built factory produces cans of beer. The owners want each can to contain exactly a certain amount.
Knowing the details of the current production process, engineers may compute the expectedExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
error in a newly produced can.
They are continuously improving the production process, so as time goes by, the expected error in a newly produced can tends to zero.
This example illustrates convergence in first-order mean.
This is a rather "technical" mode of convergence. We essentially compute a sequence of real numbers, one number for each random variable, and check if this sequence is convergentLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
in the ordinary sense.
Formal definition
If for some real number a, then {Xn} converges in rth-order mean to a.
for some real number a, then {Xn} converges in rth-order mean to a.
Commonly used notation: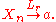
Properties
The chain of implications between the various notions of convergence are noted in their respective sections. They are, using the arrow notation:-
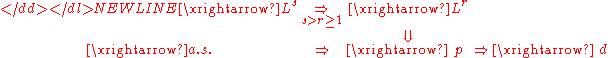
These properties, together with a number of other special cases, are summarized in the following list:
-
Almost sure convergence implies convergence in probability:[proof]-

Convergence in probability implies there exists a sub-sequence which almost surely converges:
which almost surely converges:
-

Convergence in probability implies convergence in distribution:[proof]-

Convergence in r-th order mean implies convergence in probability:-

Convergence in r-th order mean implies convergence in lower order mean, assuming that both orders are greater than one:-
 provided r ≥ s ≥ 1.
provided r ≥ s ≥ 1.
If Xn converges in distribution to a constant c, then Xn converges in probability to c:[proof]-
 provided c is a constant.
provided c is a constant.
If Xn converges in distribution to X and the difference between Xn and Yn converges in probability to zero, then Yn also converges in distribution to X:[proof]-
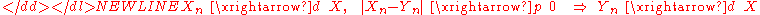
If Xn converges in distribution to X and Yn converges in distribution to a constant c, then the joint vector (Xn, Yn) converges in distribution to (X, c):[proof]
-
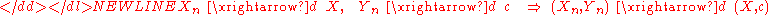 provided c is a constant.
provided c is a constant.
Note that the condition that Yn converges to a constant is important, if it were to converge to a random variable Y then we wouldn’t be able to conclude that (Xn, Yn) converges to (X, Y).
If Xn converges in probability to X and Yn converges in probability to Y, then the joint vector (Xn, Yn) converges in probability to (X, Y):[proof]
-
- If Xn converges in probability to X, and if for all n and some b, then Xn converges in rth mean to X for all r ≥ 1. In other words, if Xn converges in probability to X and all random variables Xn are almost surely bounded above and below, then Xn converges to X also in any rth mean.
- Almost sure representation. Usually, convergence in distribution does not imply convergence almost surely. However for a given sequence {Xn} which converges in distribution to X0 it is always possible to find a new probability space (Ω, F, P) and random variables {Yn, n = 0,1,…} defined on it such that Yn is equal in distribution to Xn for each n ≥ 0, and Yn converges to Y0 almost surely.
- If for all ε > 0,
- then we say that Xn converges almost completely, or almost in probability towards X. When Xn converges almost completely towards X then it also converges almost surely to X. In other words, if Xn converges in probability to X sufficiently quickly (i.e. the above sequence of tail probabilities is summable for all ε > 0), then Xn also converges almost surely to X. This is a direct implication from the Borel-Cantelli lemmaBorel-Cantelli lemmaIn probability theory, the Borel–Cantelli lemma is a theorem about sequences of events. In general, it is a result in measure theory. It is named after Émile Borel and Francesco Paolo Cantelli...
.
- If Sn is a sum of n real independent random variables:
- then Sn converges almost surely if and only if Sn converges in probability.
- The dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
gives sufficient conditions for almost sure convergence to imply L1-convergence:
-

- A necessary and sufficient condition for L1 convergence is
 and the sequence (Xn) is uniformly integrable.
and the sequence (Xn) is uniformly integrable.
See also
- Convergence of measuresConvergence of measuresIn mathematics, more specifically measure theory, there are various notions of the convergence of measures. Three of the most common notions of convergence are described below.-Total variation convergence of measures:...
- Continuous stochastic processContinuous stochastic processIn the probability theory, a continuous stochastic process is a type of stochastic process that may be said to be "continuous" as a function of its "time" or index parameter. Continuity is a nice property for a process to have, since it implies that they are well-behaved in some sense, and,...
: the question of continuity of a stochastic processStochastic processIn probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
is essentially a question of convergence, and many of the same concepts and relationships used above apply to the continuity question. - Asymptotic distributionAsymptotic distributionIn mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...
- Big O in probability notationBig O in probability notationThe order in probability notation is used in probability theory and statistical theory in direct parallel to the big-O notation which is standard in mathematics...
- Skorokhod's representation theoremSkorokhod's representation theoremIn mathematics and statistics, Skorokhod's representation theorem is a result that shows that a weakly convergent sequence of probability measures whose limit measure is sufficiently well-behaved can be represented as the distribution/law of a pointwise convergent sequence of random variables...
- A necessary and sufficient condition for L1 convergence is
-
-
- Almost sure convergence implies convergence in probability, and hence implies convergence in distribution. It is the notion of convergence used in the strong law of large numbers
-
-
-
-
- Convergence in probability implies convergence in distribution.[proof]
-
-
- Since F(a) = Pr(X ≤ a), the convergence in distribution means that the probability for Xn to be in a given range is approximately equal to the probability that the value of X is in that range, provided n is sufficiently large.
-
-
-