
Asymptotic distribution
Encyclopedia
In mathematics
and statistics
, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions. One of the main uses of the idea of an asymptotic distribution is in providing approximations to the cumulative distribution function
s of statistical estimator
s.
However, the most usual sense in which the term asymptotic distribution is used arises where the random variables Zi are modified by two sequences of non-random values. Thus if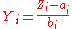
converges in distribution to a non-degenerate distribution for two sequences {ai} and {bi} then Zi is said to have that distribution as its asymptotic distribution. If the distribution function of the asymptotic distribution is F then, for large n, the following approximations hold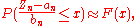
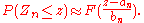
If an asymptotic distribution exists, it is not necessarily true that any one outcome of the sequence of random variables is a convergent sequence of numbers. It is the sequence of probability distributions that converges.
provides an example where the asymptotic distribution is the normal distribution.
Barndorff-Nielson & Cox provide a direct definition of asymptotic normality.
The Binomial distribution seems to be the first asymptotic approximation by a normal distribution; compared to the more general case of central limit theorem
, convergence of the Binomial to the normal is especially rapid. Asymptotic normality of the Binomial distribution is proven by the de Moivre–Laplace theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions. One of the main uses of the idea of an asymptotic distribution is in providing approximations to the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s of statistical estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
s.
Definition
A sequence of distributions corresponds to a sequence of random variables Zi for i = 1, 2, ... In the simplest case, an asymptotic distribution exists if the probability distribution of Zi converges to a probability distribution (the asymptotic distribution) as i increases: see convergence in distribution. A special case of an asymptotic distribution is when the sequence of random variables always approaches zero—that is, the Zi go to 0 as i goes to infinity. Here the asymptotic distribution is a degenerate distribution, corresponding to the value zero.However, the most usual sense in which the term asymptotic distribution is used arises where the random variables Zi are modified by two sequences of non-random values. Thus if
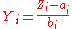
converges in distribution to a non-degenerate distribution for two sequences {ai} and {bi} then Zi is said to have that distribution as its asymptotic distribution. If the distribution function of the asymptotic distribution is F then, for large n, the following approximations hold
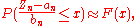
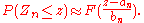
If an asymptotic distribution exists, it is not necessarily true that any one outcome of the sequence of random variables is a convergent sequence of numbers. It is the sequence of probability distributions that converges.
Asymptotic normality
Perhaps the most common distribution to arise as an asymptotic distribution is the normal distribution. In particular, the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
provides an example where the asymptotic distribution is the normal distribution.
Barndorff-Nielson & Cox provide a direct definition of asymptotic normality.
The Binomial distribution seems to be the first asymptotic approximation by a normal distribution; compared to the more general case of central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
, convergence of the Binomial to the normal is especially rapid. Asymptotic normality of the Binomial distribution is proven by the de Moivre–Laplace theorem
De Moivre–Laplace theorem
In probability theory, the de Moivre–Laplace theorem is a normal approximation to the binomial distribution. It is a special case of the central limit theorem...
.
See also
- Asymptotic theoryAsymptotic theoryAsymptotic theory or large sample theory is the branch of mathematics which studies properties of asymptotic expansions.The most known result of this field is the prime number theorem:...
- Central limit theoremCentral limit theoremIn probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
- de Moivre–Laplace theoremDe Moivre–Laplace theoremIn probability theory, the de Moivre–Laplace theorem is a normal approximation to the binomial distribution. It is a special case of the central limit theorem...
- Limiting density of discrete pointsLimiting density of discrete pointsIn information theory, the limiting density of discrete points is an adjustment to the formula of Claude Elwood Shannon for differential entropy.It was formulated by Edwin Thompson Jaynes to address defects in the initial definition of differential entropy....

