Random element
Encyclopedia
In probability theory
, random element is a generalization of the concept of random variable
to more complicated spaces than the simple real line. The concept was introduced by who commented that the “development of probability theory and expansion of area of its applications have led to necessity to pass from schemes where (random) outcomes of experience can be described by number or a finite set of numbers, to schemes where outcomes of experience represent, for example, vectors
, function
s, processes, field
s, series
, transformations, and also sets or collections of sets.”
The modern day usage of “random element” frequently assumes the space of values is a topological vector space
, often a Banach
or Hilbert space
with a specified natural sigma algebra of subsets.
, and (E, ℰ) a measurable space. A random element with values in E is a function which is (ℱ, ℰ)-measurable
. That is, a function X such that for any B ∈ ℰ the preimage of B lies in ℱ: .
Sometimes random elements with values in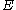
are called 
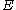-valued random variables.
Note if
, where 
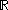are the real numbers, and 
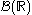is its Borel σ-algebra, then the definition of random element is the classical definition of random variable
.
The definition of a random element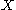
with values in a Banach space
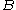is typically understood to utilize the smallest 
-algebra on B for which every bounded linear functional is measurable. An equivalent definition, in this case, to the above, is that a map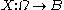 
, from a probability space, is a random element if 
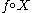is a random variable for every bounded linear functional f, or, equivalently, that 
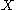is weakly measurable
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, random element is a generalization of the concept of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
to more complicated spaces than the simple real line. The concept was introduced by who commented that the “development of probability theory and expansion of area of its applications have led to necessity to pass from schemes where (random) outcomes of experience can be described by number or a finite set of numbers, to schemes where outcomes of experience represent, for example, vectors
Probability vector
Stochastic vector redirects here. For the concept of a random vector, see Multivariate random variable.In mathematics and statistics, a probability vector or stochastic vector is a vector with non-negative entries that add up to one....
, function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s, processes, field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s, series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, transformations, and also sets or collections of sets.”
The modern day usage of “random element” frequently assumes the space of values is a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
, often a Banach
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
or Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
with a specified natural sigma algebra of subsets.
Definition
Let (Ω, ℱ, P) be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, and (E, ℰ) a measurable space. A random element with values in E is a function which is (ℱ, ℰ)-measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
. That is, a function X such that for any B ∈ ℰ the preimage of B lies in ℱ: .
Sometimes random elements with values in
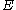are called 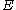-valued random variables.Note if
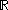, where are the real numbers, and 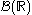is its Borel σ-algebra, then the definition of random element is the classical definition of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
.
The definition of a random element
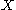with values in a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
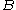is typically understood to utilize the smallest -algebra on B for which every bounded linear functional is measurable. An equivalent definition, in this case, to the above, is that a map 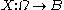, from a probability space, is a random element if 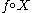is a random variable for every bounded linear functional f, or, equivalently, that 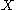is weakly measurableWeakly measurable function
In mathematics — specifically, in functional analysis — a weakly measurable function taking values in a Banach space is a function whose composition with any element of the dual space is a measurable function in the usual sense...
.
Random elements of the various nature
- Random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
- Discrete random variable
- Continuous random variable
- Complex random variable
- Simple random variable
- Random vector
- Random matrix
- Random functionRandom functionA random function is a function chosen at random from a finite family of functions. Typically, the family consists of the set of all maps from the domain to the codomain. Thus, a random function can be considered to map each input independently at random to any one of the possible outputs. Viewed...
- Random process
- Random fieldRandom fieldA random field is a generalization of a stochastic process such that the underlying parameter need no longer be a simple real or integer valued "time", but can instead take values that are multidimensional vectors, or points on some manifold....
- Random measure
- Random set
- Random closed set
- Random compact setRandom compact setIn mathematics, a random compact set is essentially a compact set-valued random variable. Random compact sets are useful in the study of attractors for random dynamical systems.-Definition:...
- Random “point”
- Random figure
- Random shape
- Random finite set
- Random finite abstract set
- Random set of events
Literature
- Hoffman-Jorgensen J., Pisier G. (1976) "Ann.Probab.", v.4, 587-589.
- Mourier E. (1955) Elements aleatoires dans un espace de Banach (These). Paris.
- Prokhorov Yu.V. (1999) Random element. Probability and Mathematical statistics. Encyclopedia. Moscow: "Great Russian Encyclopedia", P.623.