
Probability vector
Encyclopedia
Stochastic vector redirects here. For the concept of a random vector, see Multivariate random variable
.
In mathematics
and statistics
, a probability vector or stochastic vector is a vector
with non-negative entries that add up to one.
The positions (indices) of a probability vector represent the possible outcomes of a discrete random variable, and the vector gives us the probability mass function
of that random variable, which is the standard way of characterizing a discrete probability distribution.
Here are some examples of probability vectors:
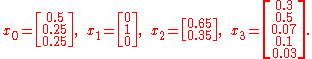
Writing out the vector components of a vector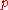 as
as
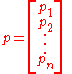
the vector components must sum to one:
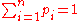
One also has the requirement that each individual component must have a probability between zero and one:
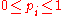
for all . These two requirements show that stochastic vectors have a geometric interpretation: A stochastic vector is a point on the "far face" of a standard orthogonal simplex
. These two requirements show that stochastic vectors have a geometric interpretation: A stochastic vector is a point on the "far face" of a standard orthogonal simplex
. That is, a stochastic vector uniquely identifies a point on the face opposite of the orthogonal corner of the standard simplex.
Some Properties of
Multivariate random variable
In mathematics, probability, and statistics, a multivariate random variable or random vector is a list of mathematical variables each of whose values is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value.More formally, a multivariate random...
.
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a probability vector or stochastic vector is a vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with non-negative entries that add up to one.
The positions (indices) of a probability vector represent the possible outcomes of a discrete random variable, and the vector gives us the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
of that random variable, which is the standard way of characterizing a discrete probability distribution.
Here are some examples of probability vectors:
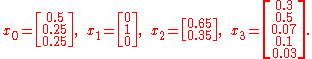
Writing out the vector components of a vector
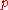 as
as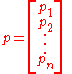
the vector components must sum to one:
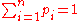
One also has the requirement that each individual component must have a probability between zero and one:
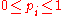
for all
 . These two requirements show that stochastic vectors have a geometric interpretation: A stochastic vector is a point on the "far face" of a standard orthogonal simplex
. These two requirements show that stochastic vectors have a geometric interpretation: A stochastic vector is a point on the "far face" of a standard orthogonal simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
. That is, a stochastic vector uniquely identifies a point on the face opposite of the orthogonal corner of the standard simplex.
Some Properties of  dimensional Probability Vectors
dimensional Probability Vectors
- Probability vectors of dimension
 are contained within an
are contained within an  dimensional unit hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
dimensional unit hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
. - The mean of a probability vector is
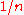 .
. - The shortest probability vector has the value
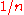 as each component of the vector, and has a length of
as each component of the vector, and has a length of 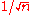 .
. - The longest probability vector has the value 1 in a single component and 0 in all others, and has a length of 1.
- The shortest vector corresponds to maximum uncertainty, the longest to maximum certainty.
- No two probability vectors in the
 dimensional unit hypersphere are collinear unless they are identical.
dimensional unit hypersphere are collinear unless they are identical. - The length of a probability vector is equal to
 ; where
; where  is the variance of the elements of the probability vector.
is the variance of the elements of the probability vector.

