Multivariate random variable
Encyclopedia
In mathematics
, probability
, and statistics
, a multivariate random variable or random vector is a list of mathematical variable
s each of whose values is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value.
More formally, a multivariate random variable is a column vector
X = (X1, ..., Xn)T (or its transpose
, which is a row vector) whose components are scalar
-valued random variable
s on the same probability space
(Ω,
, P), where Ω is the sample space, 
is the sigma-algebra
(the collection of all events), and P is the probability measure
(a function returning every event's probability
).
as the underlying sigma-algebra. This measure is also known as the joint probability distribution, the joint distribution, or the multivariate distribution of the random vector.
The distributions
of each of the component random variables Xi are called marginal distribution
s. The conditional probability distribution of Xi given Xj is the probability distribution of Xi when Xj is known to be a particular value.
, and the taking of inner products
.
or mean of a random vector X is a fixed vector E(X) whose elements are the expected values of the respective random variables.
The covariance matrix
(also called the variance-covariance matrix) of an n× 1 random vector is an n × n matrix
whose i, j element is the covariance
between the ith and the jth random variables. The covariance matrix is the expected value, element by element, of the n × n matrix computed as
[X – E(X)][X-E(X)]T, where the superscript T refers to the transpose of the indicated vector:
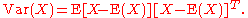
By extension, the cross-covariance matrix between two random vectors X and Y (X having n elements and Y having p elements) is the n × p matrix
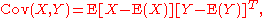
where again the indicated matrix expectation is taken element-by-element in the matrix. The cross-covariance matrix Cov(Y, X) is simply the transpose of the matrix Cov(X, Y).
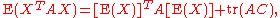
where C is the covariance matrix of X and tr refers to the trace
of a matrix — that is, to the sum of the elements on its main diagonal (from upper left to lower right). Since the quadratic form is a scalar, so is its expectation.
One can take the expectation of the product of two different quadratic forms in a zero-mean Gaussian random vector X as follows:
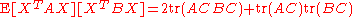
where again C is the covariance matrix of X. Again, since both quadratic forms are scalars and hence their product is a scalar, the expectation of their product is also a scalar.
, an objective often is to choose a portfolio of risky assets such that the distribution of the random portfolio return has desirable properties. For example, one might want to choose the portfolio return having the lowest variance for a given expected value. Here the random vector is the vector r of random returns on the individual assets, and the portfolio return p (a random scalar) is the inner product of the vector of random returns with a vector w of portfolio weights — the fractions of the portfolio placed in the respective assets. Since p = wTr, the expected value of the portfolio return is wTE(r) and the variance of the portfolio return can be shown to be wTCw, where C is the covariance matrix of r.
theory, we have data on n observations on a dependent variable y and n observations on each of k independent variables xj. The observations on the dependent variable are stacked into a column vector y; the observations on each independent variable are also stacked into column vectors, and these latter column vectors are combined into a matrix X of observations on the independent variables. Then the following regression equation is postulated as a description of the process that generated the data:
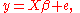
where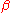
is a postulated fixed but unknown vector of k response coefficients, and e is an unknown random vector reflecting random influences on the dependent variable. By some chosen technique such as ordinary least squares
, a vector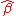
is chosen as an estimate of 
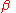, and the estimate of the vector 
, denoted 
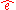, is computed as
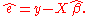
Then the statistician must analyze the properties of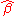
and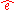 
, which are viewed as random vectors since a randomly different selection of n cases to observe would have resulted in different values for them.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a multivariate random variable or random vector is a list of mathematical variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
s each of whose values is unknown, either because the value has not yet occurred or because there is imperfect knowledge of its value.
More formally, a multivariate random variable is a column vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
X = (X1, ..., Xn)T (or its transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
, which is a row vector) whose components are scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s on the same probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω,
, P), where Ω is the sample space, is the sigma-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
(the collection of all events), and P is the probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
(a function returning every event's probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
).
Probability distribution
Every random vector gives rise to a probability measure on Rn with the Borel algebraBorel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
as the underlying sigma-algebra. This measure is also known as the joint probability distribution, the joint distribution, or the multivariate distribution of the random vector.
The distributions
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of each of the component random variables Xi are called marginal distribution
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
s. The conditional probability distribution of Xi given Xj is the probability distribution of Xi when Xj is known to be a particular value.
Operations on random vectors
Random vectors can be subjected to the same kinds of algebraic operations as can non-random vectors: addition, subtraction, multiplication by a scalarScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, and the taking of inner products
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
.
Expected value, covariance, and cross-covariance
The expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
or mean of a random vector X is a fixed vector E(X) whose elements are the expected values of the respective random variables.
The covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
(also called the variance-covariance matrix) of an n× 1 random vector is an n × n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose i, j element is the covariance
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
between the ith and the jth random variables. The covariance matrix is the expected value, element by element, of the n × n matrix computed as
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
[X – E(X)][X-E(X)]T, where the superscript T refers to the transpose of the indicated vector:
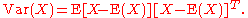
By extension, the cross-covariance matrix between two random vectors X and Y (X having n elements and Y having p elements) is the n × p matrix
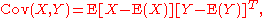
where again the indicated matrix expectation is taken element-by-element in the matrix. The cross-covariance matrix Cov(Y, X) is simply the transpose of the matrix Cov(X, Y).
Further properties
One can take the expectation of a quadratic form in the random vector X as follows: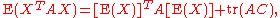where C is the covariance matrix of X and tr refers to the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of a matrix — that is, to the sum of the elements on its main diagonal (from upper left to lower right). Since the quadratic form is a scalar, so is its expectation.
One can take the expectation of the product of two different quadratic forms in a zero-mean Gaussian random vector X as follows:
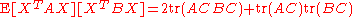
where again C is the covariance matrix of X. Again, since both quadratic forms are scalars and hence their product is a scalar, the expectation of their product is also a scalar.
Portfolio theory
In portfolio theory in financeFinance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, an objective often is to choose a portfolio of risky assets such that the distribution of the random portfolio return has desirable properties. For example, one might want to choose the portfolio return having the lowest variance for a given expected value. Here the random vector is the vector r of random returns on the individual assets, and the portfolio return p (a random scalar) is the inner product of the vector of random returns with a vector w of portfolio weights — the fractions of the portfolio placed in the respective assets. Since p = wTr, the expected value of the portfolio return is wTE(r) and the variance of the portfolio return can be shown to be wTCw, where C is the covariance matrix of r.
Regression theory
In linear regressionLinear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
theory, we have data on n observations on a dependent variable y and n observations on each of k independent variables xj. The observations on the dependent variable are stacked into a column vector y; the observations on each independent variable are also stacked into column vectors, and these latter column vectors are combined into a matrix X of observations on the independent variables. Then the following regression equation is postulated as a description of the process that generated the data:
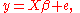
where
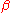is a postulated fixed but unknown vector of k response coefficients, and e is an unknown random vector reflecting random influences on the dependent variable. By some chosen technique such as ordinary least squaresOrdinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
, a vector
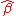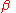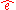is chosen as an estimate of , and the estimate of the vector , denoted , is computed as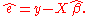Then the statistician must analyze the properties of
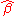and 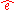, which are viewed as random vectors since a randomly different selection of n cases to observe would have resulted in different values for them.