
Continuous stochastic process
Encyclopedia
In the probability theory
, a continuous stochastic process is a type of stochastic process
that may be said to be "continuous
" as a function of its "time" or index parameter. Continuity is a nice property for (the sample paths of) a process to have, since it implies that they are well-behaved
in some sense, and, therefore, much easier to analyse. It is implicit here that the index of the stochastic process is a continuous variable. Note that some authors define a "continuous (stochastic) process" as only requiring that the index variable be continuous, without continuity of sample paths: in some terminology, this would be a continuous-time stochastic process
, in parallel to a "discrete-time process". Given the possible confusion, caution is needed.
, let T be some interval
of time, and let X : T × Ω → S be a stochastic process. For simplicity, the rest of this article will take the state space S to be the real line
R, but the definitions go through mutatis mutandis
if S is Rn, a normed vector space, or even a general metric space
.
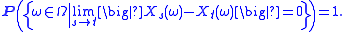
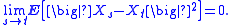
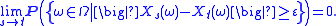
Equivalently, X is continuous in probability at time t if
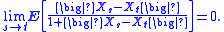
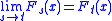
for all points x at which Ft is continuous, where Ft denotes the cumulative distribution function
of the random variable
Xt.
ω ∈ Ω. Sample continuity is the appropriate notion of continuity for processes such as Itō diffusion
s.
, continuous and Σ-measurable function
g : S → R, Ex[g(Xt)] depends continuously upon x. Here x denotes the initial state of the process X, and Ex denotes expectation conditional upon the event that X starts at x.
. In particular:
It is tempting to confuse continuity with probability one with sample continuity. Continuity with probability one at time t means that P(At) = 0, where the event At is given by
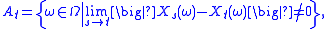
and it is perfectly feasible to check whether or not this holds for each t ∈ T. Sample continuity, on the other hand, requires that P(A) = 0, where
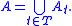
Note that A is an uncountable union
of events, so it may not actually be an event itself, so P(A) may be undefined! Even worse, even if A is an event, P(A) can be strictly positive even if P(At) = 0 for every t ∈ T. This is the case, for example, with the telegraph process
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a continuous stochastic process is a type of stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
that may be said to be "continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
" as a function of its "time" or index parameter. Continuity is a nice property for (the sample paths of) a process to have, since it implies that they are well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
in some sense, and, therefore, much easier to analyse. It is implicit here that the index of the stochastic process is a continuous variable. Note that some authors define a "continuous (stochastic) process" as only requiring that the index variable be continuous, without continuity of sample paths: in some terminology, this would be a continuous-time stochastic process
Continuous-time stochastic process
In probability theory and statistics, a continuous-time stochastic process, or a continuous-space-time stochastic process is a stochastic process for which the index variable takes a continuous set of values, as contrasted with a discrete-time process for which the index variable takes only...
, in parallel to a "discrete-time process". Given the possible confusion, caution is needed.
Definitions
Let (Ω, Σ, P) be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, let T be some interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of time, and let X : T × Ω → S be a stochastic process. For simplicity, the rest of this article will take the state space S to be the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R, but the definitions go through mutatis mutandis
Mutatis mutandis
Mutatis mutandis is a Latin phrase meaning "by changing those things which need to be changed" or more simply "the necessary changes having been made"....
if S is Rn, a normed vector space, or even a general metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
.
Continuity with probability one
Given a time t ∈ T, X is said to be continuous with probability one at t if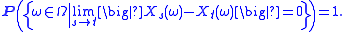
Mean-square continuity
Given a time t ∈ T, X is said to be continuous in mean-square at t if E[|Xt|2] < +∞ and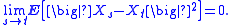
Continuity in probability
Given a time t ∈ T, X is said to be continuous in probability at t if, for all ε > 0,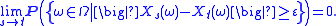
Equivalently, X is continuous in probability at time t if
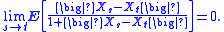
Continuity in distribution
Given a time t ∈ T, X is said to be continuous in distribution at t if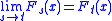
for all points x at which Ft is continuous, where Ft denotes the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of the random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
Xt.
Sample continuity
X is said to be sample continuous if Xt(ω) is continuous in t for P-almost allAlmost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
ω ∈ Ω. Sample continuity is the appropriate notion of continuity for processes such as Itō diffusion
Ito diffusion
In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
s.
Feller continuity
X is said to be a Feller-continuous process if, for any fixed t ∈ T and any boundedBounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
, continuous and Σ-measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
g : S → R, Ex[g(Xt)] depends continuously upon x. Here x denotes the initial state of the process X, and Ex denotes expectation conditional upon the event that X starts at x.
Relationships
The relationships between the various types of continuity of stochastic processes are akin to the relationships between the various types of convergence of random variablesConvergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
. In particular:
- continuity with probability one implies continuity in probability;
- continuity in mean-square implies continuity in probability;
- continuity with probability one neither implies, nor is implied by, continuity in mean-square;
- continuity in probability implies, but is not implied by, continuity in distribution.
It is tempting to confuse continuity with probability one with sample continuity. Continuity with probability one at time t means that P(At) = 0, where the event At is given by
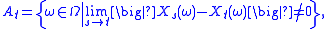
and it is perfectly feasible to check whether or not this holds for each t ∈ T. Sample continuity, on the other hand, requires that P(A) = 0, where
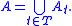
Note that A is an uncountable union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of events, so it may not actually be an event itself, so P(A) may be undefined! Even worse, even if A is an event, P(A) can be strictly positive even if P(At) = 0 for every t ∈ T. This is the case, for example, with the telegraph process
Telegraph process
In probability theory, the telegraph process is a memoryless continuous-time stochastic process that shows two distinct values.If these are called a and b, the process can be described by the following master equations:...
.

