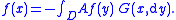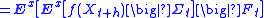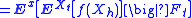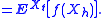Ito diffusion
Encyclopedia
In mathematics
— specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation
. That equation is similar to the Langevin equation
, used in Physics to describe the brownian motion of a particle subjected to a potential in a viscous fluid. Itō diffusions are named after the Japan
ese mathematician
Kiyoshi Itō
.
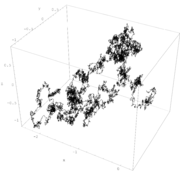A (time-homogeneous) Itō diffusion in n-dimensional Euclidean space
Rn is a process X : [0, +∞) × Ω → Rn defined on a probability space
(Ω, Σ, P) and satisfying a stochastic differential equation of the form
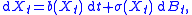
where B is an m-dimensional Brownian motion
and b : Rn → Rn and σ : Rn → Rn×m satisfy the usual Lipschitz continuity
condition
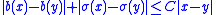
for some constant C and all x and y in Rn; this condition ensures the existence of a unique strong solution X to the stochastic differential equation given above. The vector field
b is known as the drift coefficient of X; the matrix field
σ is known as the diffusion coefficient of X. It is important to note that b and σ do not depend upon time; if they were to depend upon time, X would be referred to only as an Itō process, not a diffusion. Itō diffusions have a number of nice properties, which include
In particular, an Itō diffusion is a continuous, strongly Markovian process such that the domain of its characteristic operator includes all twice-continuously differentiable
functions, so it is a diffusion in the sense defined by Dynkin (1965).
, i.e., for almost all
realisations Bt(ω) of the noise, Xt(ω) is a continuous function
of the time parameter, t. More accurately, there is a "continuous version" of X, a continuous process Y so that
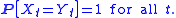
This follows from the standard existence and uniqueness theory for strong solutions of stochastic differential equations.
.
For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px.
Let f : Rn → R be a Borel-measurable function
that is bounded below
and define, for fixed t ≥ 0, u : Rn → R by
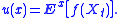
The behaviour of the function u above when the time t is varied is addressed by the Kolmogorov backward equation, the Fokker-Planck equation, et c. (See below.)
Let Σ∗ denote the natural
filtration
of (Ω, Σ) generated by the Brownian motion B: for t ≥ 0,
It is easy to show that X is adapted
to Σ∗ (i.e. each Xt is Σt-measurable), so the natural filtration F∗ = F∗X of (Ω, Σ) generated by X has Ft ⊆ Σt for each t ≥ 0.
Let f : Rn → R be a bounded, Borel-measurable function. Then, for all t and h ≥ 0, the conditional expectation
conditioned on the σ-algebra Σt and the expectation of the process "restarted" from Xt satisfy the Markov property:
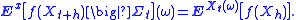
In fact, X is also a Markov process with respect to the filtration F∗, as the following shows:
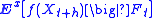
As before, let f : Rn → R be a bounded, Borel-measurable function. Let τ be a stopping time with respect to the filtration Σ∗ with τ < +∞ almost surely
. Then, for all h ≥ 0,
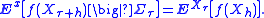
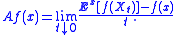
The set of all functions f for which this limit exists at a point x is denoted DA(x), while DA denotes the set of all f for which the limit exists for all x ∈ Rn. One can show that any compactly-supported C2 (twice differentiable with continuous second derivative) function f lies in DA and that
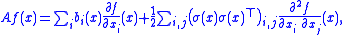
or, in terms of the gradient
and scalar
and Frobenius inner products,
,
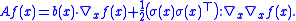
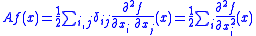i.e., A = ½Δ, where Δ denotes the Laplace operator
.
in which time t and the initial position x are the independent variables. More precisely, if f ∈ C2(Rn; R) has compact support and u : [0, +∞) × Rn → R is defined by
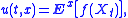
then u(t, x) is differentiable with respect to t, u(t, ·) ∈ DA for all t, and u satisfies the following partial differential equation
, known as Kolmogorov's backward equation:
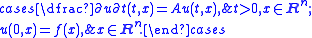
The Fokker-Planck equation (also known as Kolmogorov's forward equation) is in some sense the "adjoint
" to the backward equation, and tells us how the probability density function
s of Xt evolve with time t. Let ρ(t, ·) be the density of Xt with respect to Lebesgue measure
on Rn, i.e., for any Borel-measurable set S ⊆ Rn,
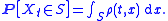
Let A∗ denote the Hermitian adjoint
of A (with respect to the L2
inner product). Then, given that the initial position X0 has a prescribed density ρ0, ρ(t, x) is differentiable with respect to t, ρ(t, ·) ∈ DA* for all t, and ρ satisfies the following partial differential equation, known as the Fokker-Planck equation:
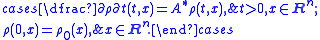
that is bounded below. Define a function v : [0, +∞) × Rn → R by
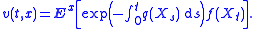
The Feynman-Kac formula states that v satisfies the partial differential equation
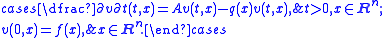
Moreover, if w : [0, +∞) × Rn → R is C1 in time, C2 in space, bounded on K × Rn for all compact K, and satisfies the above partial differential equation, then w must be v as defined above.
Kolmogorov's backward equation is the special case of the Feynman-Kac formula in which q(x) = 0 for all x ∈ Rn.
.
The characteristic operator
of an Itō diffusion X is defined by
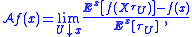
where the sets U form a sequence of open set
s Uk that decrease to the point x in the sense that
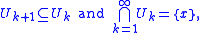
and
is the first exit time from U for X.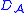
denotes the set of all f for which this limit exists for all x ∈ Rn and all sequences {Uk}. If Ex[τU] = +∞ for all open sets U containing x, define
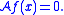
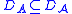
and that
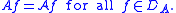
In particular, the generator and characteristic operator agree for all C2 functions f, in which case
Above, the generator (and hence characteristic operator) of Brownian motion on Rn was calculated to be ½Δ, where Δ denotes the Laplace operator. The characteristic operator is useful in defining Brownian motion on an m-dimensional Riemannian manifold
(M, g): a Brownian motion on M is defined to be a diffusion on M whose characteristic operator
in local coordinates xi, 1 ≤ i ≤ m, is given by ½ΔLB, where ΔLB is the Laplace-Beltrami operator given in local coordinates by
where [gij] = [gij]−1 in the sense of the inverse of a square matrix.
. However, if a positive multiple of the identity operator I is subtracted from A then the resulting operator is invertible. The inverse of this operator can be expressed in terms of X itself using the resolvent operator.
For α > 0, the resolvent operator Rα, acting on bounded, continuous functions g : Rn → R, is defined by
It can be shown, using the Feller continuity of the diffusion X, that Rαg is itself a bounded, continuous function. Also, Rα and αI − A are mutually inverse operators:
for an Itō diffusion X, i.e. a measure on Rn that does not change under the "flow" of X: i.e., if X0 is distributed according to such an invariant measure μ∞, then Xt is also distributed according to μ∞ for any t ≥ 0. The Fokker-Planck equation offers a way to find such a measure, at least if it has a probability density function ρ∞: if X0 is indeed distributed according to an invariant measure μ∞ with density ρ∞, then the density ρ(t, ·) of Xt does not change with t, so ρ(t, ·) = ρ∞, and so ρ∞ must solve the (time-independent) partial differential equation
This illustrates one of the connections between stochastic analysis and the study of partial differential equations. Conversely, a given second-order linear partial differential equation of the form Λf = 0 may be hard to solve directly, but if Λ = A∗ for some Itō diffusion X, and an invariant measure for X is easy to compute, then that measure's density provides a solution to the partial differential equation.
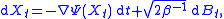
where β > 0 plays the role of an inverse temperature and Ψ : Rn → R is a scalar potential satisfying suitable smoothness and growth conditions. In this case, the Fokker-Planck equation has a unique stationary solution ρ∞ (i.e. X has a unique invariant measure μ∞ with density ρ∞) and it is given by the Gibbs distribution:
where the partition function
Z is given by
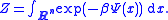
Moreover, the density ρ∞ satisfies a variational principle
: it minimizes over all probability densities ρ on Rn the free energy
functional F given by
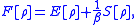
where
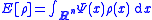
plays the role of an energy functional, and
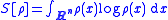
is the negative of the Gibbs-Boltzmann entropy functional. Even when the potential Ψ is not well-behaved enough for the partition function Z and the Gibbs measure μ∞ to be defined, the free energy F[ρ(t, ·)] still makes sense for each time t ≥ 0, provided that the initial condition has F[ρ(0, ·)] < +∞. The free energy functional F is, in fact, a Lyapunov function
for the Fokker-Planck equation: F[ρ(t, ·)] must decrease as t increases. Thus, F is an H-function
for the X-dynamics.
X on Rn satisfying the stochastic differential equation
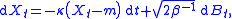
where m ∈ Rn, β > 0 and κ > 0 are given constants. In this case, the potential Ψ is given by Ψ(x) = ½κ|x − m|2, and so the invariant measure for X is a Gaussian measure
with density ρ∞ given by
.
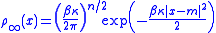Heuristically, for large t, Xt is approximately normally distributed with mean m and variance (βκ)−1. The expression for the variance may be interpreted as follows: large values of κ mean that the potential well Ψ has "very steep sides", so Xt is unlikely to move far from the minimum of Ψ at m; similarly, large values of β mean that the system is quite "cold" with little noise, so, again, Xt is unlikely to move far away from m.
. However, for any f ∈ C2(Rn; R) with compact support, the process M : [0, +∞) × Ω → R defined by
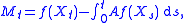
where A is the generator of X, is a martingale with respect to the natural filtration F∗ of (Ω, Σ) by X. The proof is quite simple: it follows from the usual expression of the action of the generator on smooth enough functions f and Itō's lemma
(the stochastic chain rule
) that
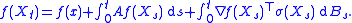
Since Itō integrals are martingales with respect to the natural filtration Σ∗ of (Ω, Σ) by B, for t > s,
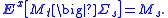
Hence, as required,
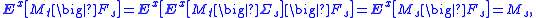
since Ms is Fs-measurable.
, gives the expected value
of any suitably smooth statistic of an Itō diffusion X (with generator A) at a stopping time. Precisely, if τ is a stopping time with Ex[τ] < +∞, and f : Rn → R is C2 with compact support, then
Dynkin's formula can be used to calculate many useful statistics of stopping times. For example, canonical Brownian motion on the real line starting at 0 exits the interval
(−R, +R) at a random time τR with expected value
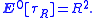
Dynkin's formula provides information about the behaviour of X at a fairly general stopping time. For more information on the distribution of X at a hitting time
, one can study the harmonic measure of the process.
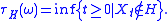
Sometimes, however, one also wishes to know the distribution of the points at which X exits the set. For example, canonical Brownian motion B on the real line starting at 0 exits the interval
(−1, +1) at −1 with probability ½ and at +1 with probability ½, so Bτ(−1, +1) is uniformly distributed on the set {−1, +1}.
In general, if G is compactly embedded
within Rn, then the harmonic measure (or hitting distribution) of X on the boundary
∂G of G is the measure μGx defined by
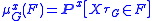
for x ∈ G and F ⊆ ∂G.
Returning to the earlier example of Brownian motion, one can show that if B is a Brownian motion in Rn starting at x ∈ Rn and D ⊂ Rn is an open ball centred on x, then the harmonic measure of B on ∂D is invariant
under all rotation
s of D about x and coincides with the normalized surface measure on ∂D.
The harmonic measure satisfies an interesting mean value property: if f : Rn → R is any bounded, Borel-measurable function and φ is given by
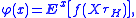
then, for all Borel sets G ⊂⊂ H and all x ∈ G,
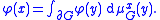
The mean value property is very useful in the solution of partial differential equations using stochastic processes
.
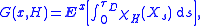
or for bounded, continuous functions f : D → R by
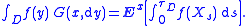
The name "Green measure" comes from the fact that if X is Brownian motion, then
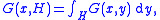
where G(x, y) is Green's function
for the operator ½Δ on the domain D.
Suppose that Ex[τD] < +∞ for all x ∈ D. Then the Green formula holds for all f ∈ C2(Rn; R) with compact support:
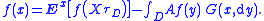
In particular, if the support of f is compactly embedded
in D,
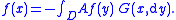
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
. That equation is similar to the Langevin equation
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
, used in Physics to describe the brownian motion of a particle subjected to a potential in a viscous fluid. Itō diffusions are named after the Japan
Japan
Japan is an island nation in East Asia. Located in the Pacific Ocean, it lies to the east of the Sea of Japan, China, North Korea, South Korea and Russia, stretching from the Sea of Okhotsk in the north to the East China Sea and Taiwan in the south...
ese mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Kiyoshi Itō
Kiyoshi Ito
was a Japanese mathematician whose work is now called Itō calculus. The basic concept of this calculus is the Itō integral, and among the most important results is Itō's lemma. The Itō calculus facilitates mathematical understanding of random events...
.
Overview
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn is a process X : [0, +∞) × Ω → Rn defined on a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω, Σ, P) and satisfying a stochastic differential equation of the form
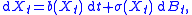
where B is an m-dimensional Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
and b : Rn → Rn and σ : Rn → Rn×m satisfy the usual Lipschitz continuity
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
condition
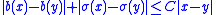
for some constant C and all x and y in Rn; this condition ensures the existence of a unique strong solution X to the stochastic differential equation given above. The vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
b is known as the drift coefficient of X; the matrix field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
σ is known as the diffusion coefficient of X. It is important to note that b and σ do not depend upon time; if they were to depend upon time, X would be referred to only as an Itō process, not a diffusion. Itō diffusions have a number of nice properties, which include
- sampleSample continuous processIn mathematics, a sample-continuous process is a stochastic process whose sample paths are almost surely continuous functions.-Definition:Let be a probability space. Let X : I × Ω → S be a stochastic process, where the index set I and state space S...
and Feller continuityFeller-continuous processIn mathematics, a Feller-continuous process is a continuous-time stochastic process for which the expected value of suitable statistics of the process at a given time in the future depend continuously on the initial condition of the process...
; - the Markov propertyMarkov propertyIn probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
; - the strong Markov property;
- the existence of an infinitesimal generatorInfinitesimal generator (stochastic processes)In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a stochastic process is a partial differential operator that encodes a great deal of information about the process...
; - the existence of a characteristic operator;
- Dynkin's formulaDynkin's formulaIn mathematics — specifically, in stochastic analysis — Dynkin's formula is a theorem giving the expected value of any suitably smooth statistic of an Itō diffusion at a stopping time. It may be seen as a stochastic generalization of the fundamental theorem of calculus...
.
In particular, an Itō diffusion is a continuous, strongly Markovian process such that the domain of its characteristic operator includes all twice-continuously differentiable
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
functions, so it is a diffusion in the sense defined by Dynkin (1965).
Sample continuity
An Itō diffusion X is a sample continuous processSample continuous process
In mathematics, a sample-continuous process is a stochastic process whose sample paths are almost surely continuous functions.-Definition:Let be a probability space. Let X : I × Ω → S be a stochastic process, where the index set I and state space S...
, i.e., for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
realisations Bt(ω) of the noise, Xt(ω) is a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of the time parameter, t. More accurately, there is a "continuous version" of X, a continuous process Y so that
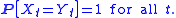
This follows from the standard existence and uniqueness theory for strong solutions of stochastic differential equations.
Feller continuity
In addition to being (sample) continuous, an Itō diffusion X satisfies the stronger requirement to be a Feller-continuous processFeller-continuous process
In mathematics, a Feller-continuous process is a continuous-time stochastic process for which the expected value of suitable statistics of the process at a given time in the future depend continuously on the initial condition of the process...
.
For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px.
Let f : Rn → R be a Borel-measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
that is bounded below
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
and define, for fixed t ≥ 0, u : Rn → R by
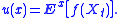
- Lower semi-continuitySemi-continuityIn mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
: if f is lower semi-continuous, then u is lower semi-continuous. - Feller continuity: if f is bounded and continuous, then u is continuous.
The behaviour of the function u above when the time t is varied is addressed by the Kolmogorov backward equation, the Fokker-Planck equation, et c. (See below.)
The Markov property
An Itō diffusion X has the important property of being Markovian: the future behaviour of X, given what has happened up to some time t, is the same as if the process had been started at the position Xt at time 0. The precise mathematical formulation of this statement requires some additional notation:Let Σ∗ denote the natural
Natural filtration
In the theory of stochastic processes in mathematics and statistics, the natural filtration associated to a stochastic process is a filtration associated to the process which records its "past behaviour" at each time...
filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
of (Ω, Σ) generated by the Brownian motion B: for t ≥ 0,
It is easy to show that X is adapted
Adapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
to Σ∗ (i.e. each Xt is Σt-measurable), so the natural filtration F∗ = F∗X of (Ω, Σ) generated by X has Ft ⊆ Σt for each t ≥ 0.
Let f : Rn → R be a bounded, Borel-measurable function. Then, for all t and h ≥ 0, the conditional expectation
Conditional expectation
In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
conditioned on the σ-algebra Σt and the expectation of the process "restarted" from Xt satisfy the Markov property:
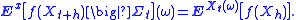
In fact, X is also a Markov process with respect to the filtration F∗, as the following shows:
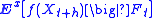
The strong Markov property
The strong Markov property is a generalization of the Markov property above in which t is replaced by a suitable random time τ : Ω → [0, +∞] known as a stopping time. So, for example, rather than "restarting" the process X at time t = 1, one could "restart" whenever X first reaches some specified point p of Rn.As before, let f : Rn → R be a bounded, Borel-measurable function. Let τ be a stopping time with respect to the filtration Σ∗ with τ < +∞ almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
. Then, for all h ≥ 0,
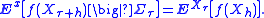
Definition
Associated to each Itō diffusion, there is a second-order partial differential operator known as the generator of the diffusion. The generator is very useful in many applications and encodes a great deal of information about the process X. Formally, the infinitesimal generator of an Itō diffusion X is the operator A, which is defined to act on suitable functions f : Rn → R by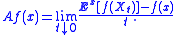The set of all functions f for which this limit exists at a point x is denoted DA(x), while DA denotes the set of all f for which the limit exists for all x ∈ Rn. One can show that any compactly-supported C2 (twice differentiable with continuous second derivative) function f lies in DA and that
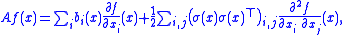
or, in terms of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and scalar
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and Frobenius inner products,
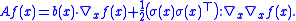
An example
The generator A for standard n-dimensional Brownian motion B, which satisfies the stochastic differential equation dXt = dBt, is given by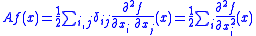,i.e., A = ½Δ, where Δ denotes the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
.
The Kolmogorov and Fokker-Planck equations
The generator is used in the formulation of Kolmogorov's backward equation. Intuitively, this equation tells us how the expected value of any suitably smooth statistic of X evolves in time: it must solve a certain partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
in which time t and the initial position x are the independent variables. More precisely, if f ∈ C2(Rn; R) has compact support and u : [0, +∞) × Rn → R is defined by
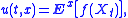
then u(t, x) is differentiable with respect to t, u(t, ·) ∈ DA for all t, and u satisfies the following partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, known as Kolmogorov's backward equation:
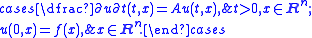
The Fokker-Planck equation (also known as Kolmogorov's forward equation) is in some sense the "adjoint
Adjoint
In mathematics, the term adjoint applies in several situations. Several of these share a similar formalism: if A is adjoint to B, then there is typically some formula of the type = .Specifically, adjoint may mean:...
" to the backward equation, and tells us how the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s of Xt evolve with time t. Let ρ(t, ·) be the density of Xt with respect to Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on Rn, i.e., for any Borel-measurable set S ⊆ Rn,
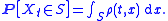
Let A∗ denote the Hermitian adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
of A (with respect to the L2
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
inner product). Then, given that the initial position X0 has a prescribed density ρ0, ρ(t, x) is differentiable with respect to t, ρ(t, ·) ∈ DA* for all t, and ρ satisfies the following partial differential equation, known as the Fokker-Planck equation:
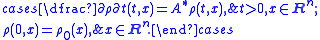
The Feynman-Kac formula
The Feynman-Kac formula is a useful generalization of Kolmogorov's backward equation. Again, f is in C2(Rn; R) and has compact support, and q : Rn → R is taken to be a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
that is bounded below. Define a function v : [0, +∞) × Rn → R by
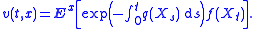
The Feynman-Kac formula states that v satisfies the partial differential equation
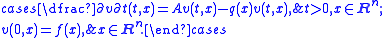
Moreover, if w : [0, +∞) × Rn → R is C1 in time, C2 in space, bounded on K × Rn for all compact K, and satisfies the above partial differential equation, then w must be v as defined above.
Kolmogorov's backward equation is the special case of the Feynman-Kac formula in which q(x) = 0 for all x ∈ Rn.
Definition
The characteristic operator of an Itō diffusion X is a partial differential operator closely related to the generator, but somewhat more general. It is more suited to certain problems, for example in the solution of the Dirichlet problemDirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
.
The characteristic operator
of an Itō diffusion X is defined by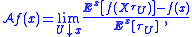where the sets U form a sequence of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s Uk that decrease to the point x in the sense that
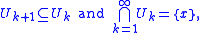
and
is the first exit time from U for X.
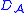denotes the set of all f for which this limit exists for all x ∈ Rn and all sequences {Uk}. If Ex[τU] = +∞ for all open sets U containing x, define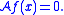Relationship with the generator
The characteristic operator and infinitesimal generator are very closely related, and even agree for a large class of functions. One can show that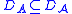and that
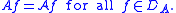
In particular, the generator and characteristic operator agree for all C2 functions f, in which case
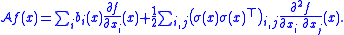
Application: Brownian motion on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(M, g): a Brownian motion on M is defined to be a diffusion on M whose characteristic operator
in local coordinates xi, 1 ≤ i ≤ m, is given by ½ΔLB, where ΔLB is the Laplace-Beltrami operator given in local coordinates by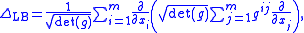where [gij] = [gij]−1 in the sense of the inverse of a square matrix.
The resolvent operator
In general, the generator A of an Itō diffusion X is not a bounded operatorBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
. However, if a positive multiple of the identity operator I is subtracted from A then the resulting operator is invertible. The inverse of this operator can be expressed in terms of X itself using the resolvent operator.
For α > 0, the resolvent operator Rα, acting on bounded, continuous functions g : Rn → R, is defined by
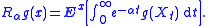
It can be shown, using the Feller continuity of the diffusion X, that Rαg is itself a bounded, continuous function. Also, Rα and αI − A are mutually inverse operators:
- if f : Rn → R is C2 with compact support, then, for all α > 0,
-
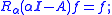
- if g : Rn → R is bounded and continuous, then Rαg lies in DA and, for all α > 0,
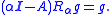
Invariant measures
Sometimes it is necessary to find an invariant measureInvariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
for an Itō diffusion X, i.e. a measure on Rn that does not change under the "flow" of X: i.e., if X0 is distributed according to such an invariant measure μ∞, then Xt is also distributed according to μ∞ for any t ≥ 0. The Fokker-Planck equation offers a way to find such a measure, at least if it has a probability density function ρ∞: if X0 is indeed distributed according to an invariant measure μ∞ with density ρ∞, then the density ρ(t, ·) of Xt does not change with t, so ρ(t, ·) = ρ∞, and so ρ∞ must solve the (time-independent) partial differential equation
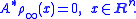
This illustrates one of the connections between stochastic analysis and the study of partial differential equations. Conversely, a given second-order linear partial differential equation of the form Λf = 0 may be hard to solve directly, but if Λ = A∗ for some Itō diffusion X, and an invariant measure for X is easy to compute, then that measure's density provides a solution to the partial differential equation.
Invariant measures for gradient flows
An invariant measure is comparatively easy to compute when the process X is a stochastic gradient flow of the form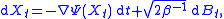where β > 0 plays the role of an inverse temperature and Ψ : Rn → R is a scalar potential satisfying suitable smoothness and growth conditions. In this case, the Fokker-Planck equation has a unique stationary solution ρ∞ (i.e. X has a unique invariant measure μ∞ with density ρ∞) and it is given by the Gibbs distribution:
where the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
Z is given by
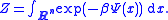
Moreover, the density ρ∞ satisfies a variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
: it minimizes over all probability densities ρ on Rn the free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
functional F given by
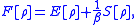
where
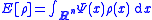
plays the role of an energy functional, and
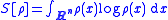
is the negative of the Gibbs-Boltzmann entropy functional. Even when the potential Ψ is not well-behaved enough for the partition function Z and the Gibbs measure μ∞ to be defined, the free energy F[ρ(t, ·)] still makes sense for each time t ≥ 0, provided that the initial condition has F[ρ(0, ·)] < +∞. The free energy functional F is, in fact, a Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
for the Fokker-Planck equation: F[ρ(t, ·)] must decrease as t increases. Thus, F is an H-function
H-theorem
In Classical Statistical Mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the increase in the entropy of an ideal gas in an irreversible process. H-theorem follows from considerations of Boltzmann's equation...
for the X-dynamics.
Example
Consider the Ornstein-Uhlenbeck processOrnstein-Uhlenbeck process
In mathematics, the Ornstein–Uhlenbeck process , is a stochastic process that, roughly speaking, describes the velocity of a massive Brownian particle under the influence of friction...
X on Rn satisfying the stochastic differential equation
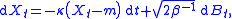
where m ∈ Rn, β > 0 and κ > 0 are given constants. In this case, the potential Ψ is given by Ψ(x) = ½κ|x − m|2, and so the invariant measure for X is a Gaussian measure
Gaussian measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
with density ρ∞ given by
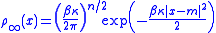.Heuristically, for large t, Xt is approximately normally distributed with mean m and variance (βκ)−1. The expression for the variance may be interpreted as follows: large values of κ mean that the potential well Ψ has "very steep sides", so Xt is unlikely to move far from the minimum of Ψ at m; similarly, large values of β mean that the system is quite "cold" with little noise, so, again, Xt is unlikely to move far away from m.
The martingale property
In general, an Itō diffusion X is not a martingaleMartingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
. However, for any f ∈ C2(Rn; R) with compact support, the process M : [0, +∞) × Ω → R defined by
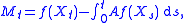
where A is the generator of X, is a martingale with respect to the natural filtration F∗ of (Ω, Σ) by X. The proof is quite simple: it follows from the usual expression of the action of the generator on smooth enough functions f and Itō's lemma
Ito's lemma
In mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō...
(the stochastic chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
) that
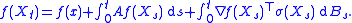
Since Itō integrals are martingales with respect to the natural filtration Σ∗ of (Ω, Σ) by B, for t > s,
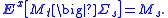
Hence, as required,
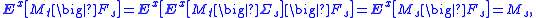
since Ms is Fs-measurable.
Dynkin's formula
Dynkin's formula, named after Eugene DynkinEugene Dynkin
Eugene Borisovich Dynkin is a Soviet and American mathematician. He has made contributions to the fields of probability and algebra, especially semisimple Lie groups, Lie algebras, and Markov processes...
, gives the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of any suitably smooth statistic of an Itō diffusion X (with generator A) at a stopping time. Precisely, if τ is a stopping time with Ex[τ] < +∞, and f : Rn → R is C2 with compact support, then
Dynkin's formula can be used to calculate many useful statistics of stopping times. For example, canonical Brownian motion on the real line starting at 0 exits the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(−R, +R) at a random time τR with expected value
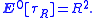
Dynkin's formula provides information about the behaviour of X at a fairly general stopping time. For more information on the distribution of X at a hitting time
Hitting time
In the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...
, one can study the harmonic measure of the process.
The harmonic measure
In many situations, it is sufficient to know when an Itō diffusion X will first leave a measurable set H ⊆ Rn. That is, one wishes to study the first exit timeHitting time
In the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...
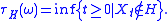
Sometimes, however, one also wishes to know the distribution of the points at which X exits the set. For example, canonical Brownian motion B on the real line starting at 0 exits the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(−1, +1) at −1 with probability ½ and at +1 with probability ½, so Bτ(−1, +1) is uniformly distributed on the set {−1, +1}.
In general, if G is compactly embedded
Compactly embedded
In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
within Rn, then the harmonic measure (or hitting distribution) of X on the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
∂G of G is the measure μGx defined by
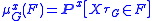
for x ∈ G and F ⊆ ∂G.
Returning to the earlier example of Brownian motion, one can show that if B is a Brownian motion in Rn starting at x ∈ Rn and D ⊂ Rn is an open ball centred on x, then the harmonic measure of B on ∂D is invariant
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
under all rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s of D about x and coincides with the normalized surface measure on ∂D.
The harmonic measure satisfies an interesting mean value property: if f : Rn → R is any bounded, Borel-measurable function and φ is given by
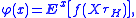
then, for all Borel sets G ⊂⊂ H and all x ∈ G,
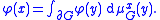
The mean value property is very useful in the solution of partial differential equations using stochastic processes
Stochastic processes and boundary value problems
In mathematics, some boundary value problems can be solved using the methods of stochastic analysis. Perhaps the most celebrated example is Shizuo Kakutani's 1944 solution of the Dirichlet problem for the Laplace operator using Brownian motion...
.
The Green measure and Green formula
Let A be a partial differential operator on a domain D ⊆ Rn and let X be an Itō diffusion with A as its generator. Intuitively, the Green measure of a Borel set H is the expected length of time that X stays in H before it leaves the domain D. That is, the Green measure of X with respect to D at x, denoted G(x, ·), is defined for Borel sets H ⊆ Rn by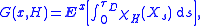or for bounded, continuous functions f : D → R by
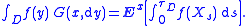
The name "Green measure" comes from the fact that if X is Brownian motion, then
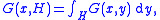
where G(x, y) is Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
for the operator ½Δ on the domain D.
Suppose that Ex[τD] < +∞ for all x ∈ D. Then the Green formula holds for all f ∈ C2(Rn; R) with compact support:
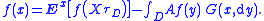
In particular, if the support of f is compactly embedded
Compactly embedded
In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
in D,