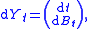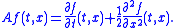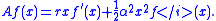Infinitesimal generator (stochastic processes)
Encyclopedia
In mathematics
— specifically, in stochastic analysis — the infinitesimal generator of a stochastic process is a partial differential operator that encodes a great deal of information about the process. The generator is used in evolution equations such as the Kolmogorov backward equation
(which describes the evolution of statistics of the process); its L2
Hermitian adjoint
is used in evolution equations such as the Fokker-Planck equation
(which describes the evolution of the probability density function
s of the process).
(Ω, Σ, P) be an Itô diffusion
satisfying a stochastic differential equation
of the form
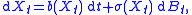
where B is an m-dimensional Brownian motion
and b : Rn → Rn and σ : Rn → Rn×m are the drift and diffusion fields respectively. For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px.
The infinitesimal generator of X is the operator A, which is defined to act on suitable functions f : Rn → R by
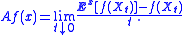
The set of all functions f for which this limit exists at a point x is denoted DA(x), while DA denotes the set of all f for which the limit exists for all x ∈ Rn. One can show that any compactly-supported C2 (twice differentiable
with continuous
second derivative) function f lies in DA and that
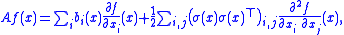
or, in terms of the gradient
and scalar
and Frobenius inner products,
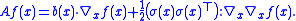
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in stochastic analysis — the infinitesimal generator of a stochastic process is a partial differential operator that encodes a great deal of information about the process. The generator is used in evolution equations such as the Kolmogorov backward equation
Kolmogorov backward equation
The Kolmogorov backward equation and its adjoint sometimes known as the Kolmogorov forward equation are partial differential equations that arise in the theory of continuous-time continuous-state Markov processes. Both were published by Andrey Kolmogorov in 1931...
(which describes the evolution of statistics of the process); its L2
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
Hermitian adjoint
Hermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
is used in evolution equations such as the Fokker-Planck equation
Fokker-Planck equation
The Fokker–Planck equation describes the time evolution of the probability density function of the velocity of a particle, and can be generalized to other observables as well.It is named after Adriaan Fokkerand Max Planck...
(which describes the evolution of the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s of the process).
Definition
Let X : [0, +∞) × Ω → Rn defined on a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω, Σ, P) be an Itô diffusion
Ito diffusion
In mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
satisfying a stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
of the form
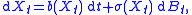
where B is an m-dimensional Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
and b : Rn → Rn and σ : Rn → Rn×m are the drift and diffusion fields respectively. For a point x ∈ Rn, let Px denote the law of X given initial datum X0 = x, and let Ex denote expectation with respect to Px.
The infinitesimal generator of X is the operator A, which is defined to act on suitable functions f : Rn → R by
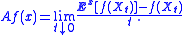
The set of all functions f for which this limit exists at a point x is denoted DA(x), while DA denotes the set of all f for which the limit exists for all x ∈ Rn. One can show that any compactly-supported C2 (twice differentiable
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
with continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
second derivative) function f lies in DA and that
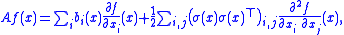
or, in terms of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and scalar
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and Frobenius inner products,
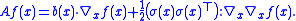
Generators of some common processes
- Standard Brownian motion on Rn, which satisfies the stochastic differential equation dXt = dBt, has generator ½Δ, where Δ denotes the Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
.
- The two-dimensional process Y satisfying
- where B is a one-dimensional Brownian motion, can be thought of as the graph of that Brownian motion, and has generator
- The Ornstein-Uhlenbeck processOrnstein-Uhlenbeck processIn mathematics, the Ornstein–Uhlenbeck process , is a stochastic process that, roughly speaking, describes the velocity of a massive Brownian particle under the influence of friction...
on R, which satisfies the stochastic differential equation dXt = μXt dt + σ dBt, has generator
- Similarly, the graph of the Ornstein-Uhlenbeck process has generator
- A geometric Brownian motionGeometric Brownian motionA geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
on R, which satisfies the stochastic differential equation dXt = rXt dt + αXt dBt, has generator