Fokker-Planck equation - AbsoluteAstronomy.com

The Fokker–Planck equation describes the time evolution

Time evolution

Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...

of the probability density function

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

of the velocity of a particle, and can be generalized to other observables as well.
It is named after Adriaan Fokker

Adriaan Fokker

Adriaan Daniël Fokker , was a Dutch physicist and musician.Fokker was born in Buitenzorg, Dutch East Indies ; he was a cousin of the aeronautical engineer Anthony Fokker...

and Max Planck

Max Planck

Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...

and is also known as the Kolmogorov forward equation (diffusion), named after Andrey Kolmogorov

Andrey Kolmogorov

Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...

, who first introduced it in a 1931 paper.
When applied to particle position distributions, it is better known as the Smoluchowski equation

Smoluchowski equation

In physics, the diffusion equation with drift term is often called Smoluchowski equation .- The equation :Let w be a density, D a diffusion constant, ζ a friction coefficient,...

.

The first consistent microscopic derivation of the Fokker–Planck equation in the single scheme of classical and quantum mechanics was performed
by Nikolay Bogoliubov and Nikolay Krylov

Nikolay Mitrofanovich Krylov

Nikolay Mitrofanovich Krylov was a Russian and Soviet mathematician known for works on interpolation, non-linear mechanics, and numerical methods for solving equations of mathematical physics.-Biography:...

.

In one spatial dimension x, the Fokker–Planck equation for a process

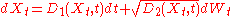with Ito drift D₁(x,t) and diffusion D₂(x,t) is: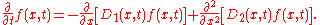

More generally, the time-dependent probability distribution may depend on a set of

macrovariables

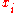. The general form of the Fokker–Planck equation is then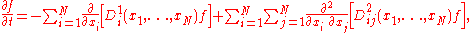

where

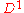is the drift vector and

the diffusion

Diffusion

Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...

tensor

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

; the latter results from the presence of the stochastic force.

Relationship with stochastic differential equations

The Fokker–Planck equation can be used for computing the probability density

Probability density

Probability density may refer to:* Probability density function in probability theory* The product of the probability amplitude with its complex conjugate in quantum mechanics...

for a stochastic process

Stochastic process

In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

described by a stochastic differential equation

Stochastic differential equation

A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....

. Consider the Itō

Ito calculus

Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....

stochastic differential equation

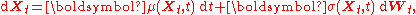
where

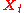is an N-dimensional random variable and

is a standard M-dimensional Wiener process

Wiener process

In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...

. The probability density

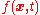for the random variable

satisfies the Fokker–Planck equation with the drift and diffusion terms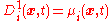

Similarly, a Fokker–Planck equation can be derived for the Stratonovich

Stratonovich integral

In stochastic processes, the Stratonovich integral is a stochastic integral, the most common alternative to the Itō integral...

stochastic differential equation

Stochastic differential equation

A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....

s that physicists and engineers generally prefer. In this case, noise-induced drift terms appear if the noise strength is state-dependent.

Examples

A standard scalar Wiener process

Wiener process

In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...

is generated by the stochastic differential equation

Stochastic differential equation

A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....

Here the drift term is zero and the diffusion coefficient is 1/2; thus the corresponding Fokker–Planck equation is

that is the simplest form of diffusion equation. If the initial condition is

, the solution is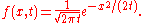

Computational considerations

Brownian motion follows the Langevin equation

Langevin equation

In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...

, which can be solved for many different stochastic forcings with results being averaged (the Monte Carlo method

Monte Carlo method

Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...

, canonical ensemble in molecular dynamics

Molecular dynamics

Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...

). However, instead of this computationally intensive approach, one can use the Fokker–Planck equation and consider the probability

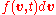of the particle having a velocity in the interval

when it starts its motion with

at time 0.

Solution

Being a partial differential equation

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

, the Fokker–Planck equation can be solved analytically only in special cases. A formal analogy of the Fokker–Planck equation with the Schrödinger equation

Schrödinger equation

The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....

allows the use of advanced operator techniques known from quantum mechanics for its solution in a number of cases.
In many applications, one is only interested in the steady-state probability distribution

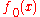, which can be found from

.
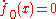The computation of mean first passage times and splitting probabilities can be reduced to the solution of an ordinary differential equation which is intimately related to the Fokker–Planck equation.

Particular cases with known solution and inversion

In mathematical finance

Mathematical finance

Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...

for volatility smile

Volatility Smile

In finance, the volatility smile is a long-observed pattern in which at-the-money options tend to have lower implied volatilities than in- or out-of-the-money options. The pattern displays different characteristics for different markets and results from the probability of extreme moves...

modeling of options via local volatility

Local volatility

A local volatility model, in mathematical finance and financial engineering, is one which treats volatility as a function of the current asset level S_t and of time t .-Formulation:...

, one has the problem of deriving a diffusion coefficient

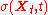consistent with a probability density obtained from market option quotes. The problem is therefore an inversion of the Fokker Planck–equation: Given the density f(x,t) of the option underlying X deduced from the option market, one aims at finding the local volatility

consistent with f. This is an inverse problem

Inverse problem

An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...

that has been solved in general by Dupire (1994, 1997) with a non-parametric solution. Brigo and Mercurio (2002, 2003) propose a solution in parametric form via a particular local volatility

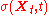consistent with a solution of the Fokker–Planck equation given by a mixture model

Mixture model

In statistics, a mixture model is a probabilistic model for representing the presence of sub-populations within an overall population, without requiring that an observed data-set should identify the sub-population to which an individual observation belongs...

. More information is available also in Fengler (2008), Gatheral (2008) and Musiela and Rutkowski (2008).

Fokker–Planck equation and path integral

Every Fokker–Planck equation is equivalent to a path integral

Path integral formulation

The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...

. The path integral formulation is an excellent starting point for the application of field theory methods. This is used, for instance, in critical dynamics.

A derivation of the path integral is possible in the same way as in quantum mechanics, simply because the Fokker–Planck equation is formally equivalent to the Schrödinger equation

Schrödinger equation

. Here are the steps for a Fokker–Planck equation with one variable x.
Write the FP equation in the form

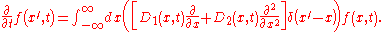
Integrate over a time interval

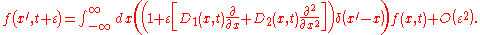
Insert the Fourier integral

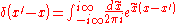
for the

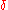-function,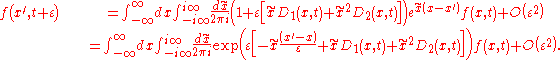

This equation expresses

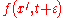as functional of

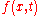. Iterating

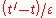times and performing the limit

gives a path integral

Path integral formulation

The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...

with Lagrangian

Lagrangian

The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...

The variables

conjugate to

are called "response variables".

Although formally equivalent, different problems may be solved more easily in the Fokker–Planck equation or the path integral formulation. The equilibrium distribution for instance may be obtained more directly from the Fokker–Planck equation.

External links

Fokker–Planck equation on the Earliest known uses of some of the words of mathematics

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Relationship with stochastic differential equations

Examples

Computational considerations

Solution

Particular cases with known solution and inversion

Fokker–Planck equation and path integral

See also

Further reading

External links