
Boltzmann equation
Encyclopedia
The Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann
, describes the statistical distribution
of one particle in rarefied gas
. It is one of the most important equations of non-equilibrium statistical mechanics, the area of statistical mechanics
that deals with systems far from thermodynamic equilibrium
; for instance, when there is an applied temperature
gradient or electric field
. The Boltzmann equation is used to study how a gas or fluid transports physical quantities such as heat
and momentum
, and thus to derive transport properties such as viscosity
, and thermal conductivity
. The problem of existence and uniqueness of solutions to the Boltzmann equation is still not fully resolved but the recent results are quite promising.
(t) evolution of the distribution (properly a density) function f(x, p, t) in one-particle phase space
, where x and p are position and momentum
, respectively. The distribution is defined so that

is the number of molecules which, at time t, have positions lying within a volume element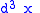 about x and momenta lying within a momentum-space element
about x and momenta lying within a momentum-space element 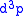 about p.
about p.
Consider those particles described by f experiencing an external force F. Then f must satisfy, in absence of collisions,
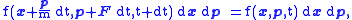
because particles at with momentum
with momentum 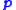 at time
at time  , will (all) be at
, will (all) be at 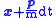 with momentum
with momentum 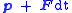 at time
at time 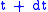 .
.
However, since collisions do occur, the particle density in the phase-space volume dx dp changes.

Dividing the equation by dx dp dt and taking the limit, we can get the Boltzmann equation
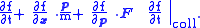
F(x, t) is the force field
acting on the particles in the fluid, and m is the mass
of the particles. The term on the right hand side is added to describe the effect of collisions between particles; if it is zero then the particles do not collide. The collisionless Boltzmann equation is often mistakenly called the Liouville equation
(the Liouville Equation is an N-particle equation).
was to determine the collision term resulting solely from two-body collisions between particles that are assumed to be uncorrelated prior to the collision. This assumption was referred to by Boltzmann as the 'Stosszahl Ansatz', and is also known as the 'molecular chaos assumption
'. Under this assumption the collision term can be written as a momentum-space integral over the product of one-particle distribution functions: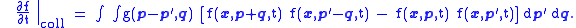
Boltzmann equations for systems in which a number of particle species can collide and produce different species. This is how the formation of the light elements in big bang nucleosynthesis
is calculated. The Boltzmann equation is also often used in dynamics, especially galactic dynamics. A galaxy, under certain assumptions, may be approximated as a continuous fluid; its mass distribution is then represented by f; in galaxies, physical collisions between the stars are very rare, and the effect of gravitational collisions can be neglected for times far longer than the age of the universe
.
In Hamiltonian mechanics
, the Boltzmann equation is often written more generally as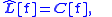
where L is the Liouville operator describing the evolution of a phase space volume and C is the collision operator. The non-relativistic form of L is
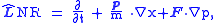
and the generalization to (general) relativity is

where Γ is the Christoffel symbol
.
Ludwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
, describes the statistical distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of one particle in rarefied gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
. It is one of the most important equations of non-equilibrium statistical mechanics, the area of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
that deals with systems far from thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
; for instance, when there is an applied temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
gradient or electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
. The Boltzmann equation is used to study how a gas or fluid transports physical quantities such as heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, and thus to derive transport properties such as viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
, and thermal conductivity
Thermal conductivity
In physics, thermal conductivity, k, is the property of a material's ability to conduct heat. It appears primarily in Fourier's Law for heat conduction....
. The problem of existence and uniqueness of solutions to the Boltzmann equation is still not fully resolved but the recent results are quite promising.
Overview
The Boltzmann equation is an equation for the timeTime
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
(t) evolution of the distribution (properly a density) function f(x, p, t) in one-particle phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
, where x and p are position and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, respectively. The distribution is defined so that

is the number of molecules which, at time t, have positions lying within a volume element
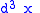 about x and momenta lying within a momentum-space element
about x and momenta lying within a momentum-space element 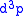 about p.
about p.Consider those particles described by f experiencing an external force F. Then f must satisfy, in absence of collisions,
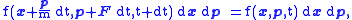
because particles at
 with momentum
with momentum 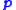 at time
at time  , will (all) be at
, will (all) be at 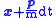 with momentum
with momentum 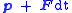 at time
at time 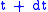 .
.However, since collisions do occur, the particle density in the phase-space volume dx dp changes.

Dividing the equation by dx dp dt and taking the limit, we can get the Boltzmann equation
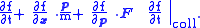
F(x, t) is the force field
Force field (chemistry)
In the context of molecular modeling, a force field refers to the form and parameters of mathematical functions used to describe the potential energy of a system of particles . Force field functions and parameter sets are derived from both experimental work and high-level quantum mechanical...
acting on the particles in the fluid, and m is the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the particles. The term on the right hand side is added to describe the effect of collisions between particles; if it is zero then the particles do not collide. The collisionless Boltzmann equation is often mistakenly called the Liouville equation
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
(the Liouville Equation is an N-particle equation).
Molecular chaos and the collision term (Stosszahl Ansatz)
The above Boltzmann equation is of little practical use as it leaves the collision term unspecified. A key insight applied by BoltzmannLudwig Boltzmann
Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...
was to determine the collision term resulting solely from two-body collisions between particles that are assumed to be uncorrelated prior to the collision. This assumption was referred to by Boltzmann as the 'Stosszahl Ansatz', and is also known as the 'molecular chaos assumption
Molecular chaos
In kinetic theory in physics, molecular chaos is the assumption that the velocities of colliding particles are uncorrelated, and independent of position...
'. Under this assumption the collision term can be written as a momentum-space integral over the product of one-particle distribution functions:
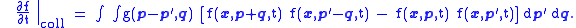
Extensions and applications
It is also possible to write down relativisticTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
Boltzmann equations for systems in which a number of particle species can collide and produce different species. This is how the formation of the light elements in big bang nucleosynthesis
Big Bang nucleosynthesis
In physical cosmology, Big Bang nucleosynthesis refers to the production of nuclei other than those of H-1 during the early phases of the universe...
is calculated. The Boltzmann equation is also often used in dynamics, especially galactic dynamics. A galaxy, under certain assumptions, may be approximated as a continuous fluid; its mass distribution is then represented by f; in galaxies, physical collisions between the stars are very rare, and the effect of gravitational collisions can be neglected for times far longer than the age of the universe
Age of the universe
The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model...
.
In Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, the Boltzmann equation is often written more generally as
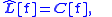
where L is the Liouville operator describing the evolution of a phase space volume and C is the collision operator. The non-relativistic form of L is
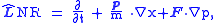
and the generalization to (general) relativity is

where Γ is the Christoffel symbol
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
.
See also
- H-theoremH-theoremIn Classical Statistical Mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the increase in the entropy of an ideal gas in an irreversible process. H-theorem follows from considerations of Boltzmann's equation...
- Fokker–Planck equation
- Navier–Stokes equations
- Vlasov equationVlasov equationThe Vlasov equation is a differential equation describing time evolution of the distribution function of plasma consisting of charged particles with long-range interaction...
- Vlasov–Poisson equation
- Lattice Boltzmann methodsLattice Boltzmann methodsLattice Boltzmann methods is a class of computational fluid dynamics methods for fluid simulation. Instead of solving the Navier–Stokes equations, the discrete Boltzmann equation is solved to simulate the flow of a Newtonian fluid with collision models such as Bhatnagar-Gross-Krook...

