Local volatility
Encyclopedia
A local volatility model, in mathematical finance
and financial engineering, is one which treats volatility
as a function of the current asset level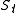
and of time 
.
, the assets St which underlie
financial derivatives, are typically assumed to follow stochastic differential equation
s of the type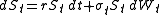
where r is the instantaneous risk free rate
, giving an average local direction to the dynamics, and W is a Wiener process
, representing the inflow of randomness into the dynamics. The amplitude of this randomness is measured by the instant volatility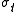
. In the simplest (naive) model, this instant volatility is assumed to be constant, but in reality realized volatility of an underlier actually rises and falls over time.
When such volatility has a randomness of its own—often described by a different equation driven by a different W—the model above is called a stochastic volatility
model. And when such volatility is merely a function of the current asset level St and of time t, we have a local volatility model. The local volatility model is a useful simplification of the stochastic volatility
model.
"Local volatility" is thus a term used in quantitative finance to denote the set of diffusion coefficients,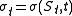
, that are consistent with market prices for all options on a given underlying. This model is used to calculate exotic option
valuations which are consistent with observed prices of vanilla options.
and Emanuel Derman
and Iraj Kani
noted that there is a unique diffusion process consistent with the risk neutral densities derived from the market prices of European options.
Derman and Kani described and implemented a local volatility function to model instantaneous volatility. They used this function at each node in a binomial options pricing model
. The tree successfully produced option valuations consistent with all market prices across strikes and expirations. The Derman-Kani model was thus formulated with discrete time and stock-price steps. The key continuous-time equations used in local volatility models were developed by Bruno Dupire
in 1994. Dupire's equation states
models.
Local volatility models have a number of attractive features . Because the only source of randomness is the stock price, local volatility models are easy to calibrate. Also, they lead to complete markets where hedging can be based only on the underlying asset. The general non-parametric approach by Dupire is however problematic, as one needs to arbitrarily pre-interpolate the input implied volatility surface before applying the method. Alternative parametric approaches have been proposed, notably the highly tractable mixture dynamical local volatility models by Damiano Brigo
and Fabio Mercurio
.
Since in local volatility models the volatility is a deterministic function of the random stock price, local volatility models are not very well used to price cliquet options or forward start options, whose values depend specifically on the random nature of volatility itself.
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
and financial engineering, is one which treats volatility
Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
as a function of the current asset level
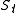and of time .Formulation
In mathematical financeMathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
, the assets St which underlie
Underlying
In finance, the underlying of a derivative is an asset, basket of assets, index, or even another derivative, such that the cash flows of the derivative depend on the value of this underlying...
financial derivatives, are typically assumed to follow stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
s of the type
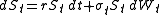
where r is the instantaneous risk free rate
Risk-free interest rate
Risk-free interest rate is the theoretical rate of return of an investment with no risk of financial loss. The risk-free rate represents the interest that an investor would expect from an absolutely risk-free investment over a given period of time....
, giving an average local direction to the dynamics, and W is a Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
, representing the inflow of randomness into the dynamics. The amplitude of this randomness is measured by the instant volatility
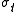. In the simplest (naive) model, this instant volatility is assumed to be constant, but in reality realized volatility of an underlier actually rises and falls over time.When such volatility has a randomness of its own—often described by a different equation driven by a different W—the model above is called a stochastic volatility
Stochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
model. And when such volatility is merely a function of the current asset level St and of time t, we have a local volatility model. The local volatility model is a useful simplification of the stochastic volatility
Stochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
model.
"Local volatility" is thus a term used in quantitative finance to denote the set of diffusion coefficients,
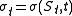, that are consistent with market prices for all options on a given underlying. This model is used to calculate exotic optionExotic option
In finance, an exotic option is a derivative which has features making it more complex than commonly traded products . These products are usually traded over-the-counter , or are embedded in structured notes....
valuations which are consistent with observed prices of vanilla options.
Development
The concept of a local volatility was developed when Bruno DupireBruno Dupire
-Local volatility:Dupire is best known for showing how to derive a local volatility model consistent with a surface of option prices across strikes and maturities, establishing the so called Dupire's approach to local volatility for modeling the volatility smile....
and Emanuel Derman
Emanuel Derman
Emanuel Derman is a South African-born academic, businessman and writer. He is best known as a quantitative analyst, and author of the book My Life as A Quant: Reflections on Physics and Finance....
and Iraj Kani
noted that there is a unique diffusion process consistent with the risk neutral densities derived from the market prices of European options.
Derman and Kani described and implemented a local volatility function to model instantaneous volatility. They used this function at each node in a binomial options pricing model
Binomial options pricing model
In finance, the binomial options pricing model provides a generalizable numerical method for the valuation of options. The binomial model was first proposed by Cox, Ross and Rubinstein in 1979. Essentially, the model uses a “discrete-time” model of the varying price over time of the underlying...
. The tree successfully produced option valuations consistent with all market prices across strikes and expirations. The Derman-Kani model was thus formulated with discrete time and stock-price steps. The key continuous-time equations used in local volatility models were developed by Bruno Dupire
Bruno Dupire
-Local volatility:Dupire is best known for showing how to derive a local volatility model consistent with a surface of option prices across strikes and maturities, establishing the so called Dupire's approach to local volatility for modeling the volatility smile....
in 1994. Dupire's equation states
Use
Local volatility models are useful in any options market in which the underlying's volatility is predominantly a function of the level of the underlying, interest-rate derivatives for example. Time-invariant local volatilities are supposedly inconsistent with the dynamics of the equity index implied volatility surface, but see , who claims that such models provide the best average hedge for equity index options. Local volatility models are nonetheless useful in the formulation of stochastic volatilityStochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
models.
Local volatility models have a number of attractive features . Because the only source of randomness is the stock price, local volatility models are easy to calibrate. Also, they lead to complete markets where hedging can be based only on the underlying asset. The general non-parametric approach by Dupire is however problematic, as one needs to arbitrarily pre-interpolate the input implied volatility surface before applying the method. Alternative parametric approaches have been proposed, notably the highly tractable mixture dynamical local volatility models by Damiano Brigo
Damiano Brigo
Damiano Brigo is an applied mathematician, and current Gilbart Chair of Financial Mathematics at King's College, London, known for a number of results in systems theory, probability and mathematical finance.-Main results:...
and Fabio Mercurio
Fabio Mercurio
Fabio Mercurio is an Italian mathematician, internationally known for a number of results in mathematical finance.-Main results:...
.
Since in local volatility models the volatility is a deterministic function of the random stock price, local volatility models are not very well used to price cliquet options or forward start options, whose values depend specifically on the random nature of volatility itself.