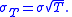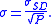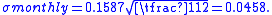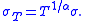Volatility (finance)
Encyclopedia
In finance
, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices. An implied volatility
is derived from the market price of a market traded derivative (in particular an option).
It is common for discussions to talk about the volatility of a security's price, even while it is the returns' volatility that is being measured. It is used to quantify the risk
of the financial instrument over the specified time period. Volatility is normally expressed in annualized terms, and it may either be an absolute number ($5) or a fraction of the mean (5%).
For a financial instrument whose price follows a Gaussian
random walk
, or Wiener process
, the width of the distribution increases as time increases. This is because there is an increasing probability
that the instrument's price will be farther away from the initial price as time increases. However, rather than increase linearly, the volatility increases with the square-root of time as time increases, because some fluctuations are expected to cancel each other out, so the most likely deviation after twice the time will not be twice the distance from zero.
Since observed price changes do not follow Gaussian distributions, others such as the Lévy distribution are often used. These can capture attributes such as "fat tail
s".
Easley, López de Prado and O'Hara (2010) argue that at least one source of volatility can be explained by Market microstructure
theory, as the result of the liquidity provision process. When market makers infer the possibility of Adverse selection
, they adjust their trading ranges, which in turn increases the band of price oscillation. If the level of toxicity surprises market makers, they may opt to vanish from the market altogether, leading to exacerbated price moves such as the so called 2010 Flash Crash.
In today's markets, it is also possible to trade volatility directly, through the use of derivative securities such as options
and variance swap
s. See Volatility arbitrage
.
(or variance
), all differences are squared, so that negative and positive differences are combined into one quantity. Two instruments with different volatilities may have the same expected return, but the instrument with higher volatility will have larger swings in values over a given period of time.
For example, a lower volatility stock may have an expected (average) return of 7%, with annual volatility of 5%. This would indicate returns from approximately negative 3% to positive 17% most of the time (19 times out of 20, or 95% via a two standard deviation
rule). A higher volatility stock, with the same expected return of 7% but with annual volatility of 20%, would indicate returns from approximately negative 33% to positive 47% most of the time (19 times out of 20, or 95%). These estimates assume a normal distribution; in reality stocks are found to be leptokurtotic
.
's Local Volatility
, Poisson Process
where volatility jumps to new levels with a predictable frequency, and the increasingly popular Heston model of Stochastic Volatility
.
It's common knowledge that types of assets experience periods of high and low volatility. That is, during some periods prices go up and down quickly, while during other times they might not seem to move at all.
Periods when prices fall quickly (a crash
) are often followed by prices going down even more, or going up by an unusual amount. Also, a time when prices rise quickly (a bubble) may often be followed by prices going up even more, or going down by an unusual amount.
The converse behavior, 'doldrums' can last for a long time as well.
Most typically, extreme movements do not appear 'out of nowhere'; they're presaged by larger movements than usual.
This is termed autoregressive conditional heteroskedasticity
.
Of course, whether such large movements have the same direction, or the opposite, is more difficult to say. And an increase in volatility does not always presage a further increase—the volatility may simply go back down again.
The generalized volatility σT for time horizon T in years is expressed as:
Therefore, if the daily logarithmic returns of a stock have a standard deviation of σSD and the time period of returns is P, the annualized volatility is
A common assumption is that P = 1/252 (there are 252 trading days in any given year). Then, if σSD = 0.01 the annualized volatility is
The monthly volatility (i.e., T = 1/12 of a year) would be
The formula used above to convert returns or volatility measures from one time period to another assume a particular underlying model or process. These formulas are accurate extrapolations of a random walk
, or Wiener process, whose steps have finite variance. However, more generally, for natural stochastic processes, the precise relationship between volatility measures for different time periods is more complicated. Some use the Lévy stability exponent α to extrapolate natural processes:
If α = 2 you get the Wiener process
scaling relation, but some people believe α < 2 for financial activities such as stocks, indexes and so on. This was discovered by Benoît Mandelbrot
, who looked at cotton prices and found that they followed a Lévy alpha-stable distribution with α = 1.7. (See New Scientist, 19 April 1997.)
To annualize this, you can use the "rule of 16", that is, multiply by 16 to get 16% as the annual volatility. The rationale for this is that 16 is the square root of 256, which is approximately the number of trading days in a year (252). This also uses the fact that the standard deviation of the sum of n independent variables (with equal standard deviations) is √n times the standard deviation of the individual variables.
Of course, the average magnitude of the observations is merely an approximation of the standard deviation of the market index. Assuming that the market index daily changes are normally distributed with mean zero and standard deviation σ, the expected value of the magnitude of the observations
is √(2/π)σ = 0.798σ. The net effect is that this crude approach underestimates the true volatility by about 20%.
:
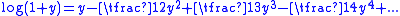
Taking only the first two terms one has:
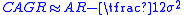
Realistically, most financial assets have negative skewness and leptokurtosis, so this formula tends to be over-optimistic. Some people use the formula:
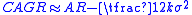
for a rough estimate, where k is an empirical factor (typically five to ten).
to dismiss volatility forecasting models. It is interesting to note that while critics are publishing their papers in top journals such as Journal of Finance
, Journal of Derivatives, Journal of Portfolio Management
, etc. those defending their volatility forecasting models or criticizing skeptics have been unable to publish their work in journals of similar prestige, in many cases opting for leaving them unpublished, as working paper
s.
Besides this controversy between believers in volatility forecasting models and the large majority of skeptics, there is a contentious battle among those same believers, one claiming that his model is superior to the rest. In August 2008, Torben Andersen and Prof. Oleg Bondarenko once again surprised the academic community by claiming not only that their volatility forecasting model was superior, but that they have mathematically demonstrated that future research was futile, since no future volatility forecasting model can beat theirs.
In an interview regarding their CIV model, Andersen and Bondarenko go as far as to assert
Removed from this controversy, practitioners and portfolio managers seem to completely ignore or dismiss volatility forecasting models. For example, Nassim Taleb
famously titled one of his Journal of Portfolio Management
papers We Don't Quite Know What We are Talking About When We Talk About Volatility. Nassim Taleb
gained worldwide recognition through his Black swan theory
, which argues the sillines of trying to predict the unpredictable.
In a similar note, Emanuel Derman
expressed his disillusion with the enormous supply of empirical models unsupported by any theory. He argues that, while "theories are attempts to uncover the hidden principles underpinning the world around us, as Albert Einstein did with his theory of relativity", we should remember that "models are metaphors -- analogies that describe one thing relative to another". From that perspective, volatility forecasting models are nothing more than high-tech horoscopes: Even if they were successful predictors (which they are not), they would not add anything to our understanding of the principles governing the markets.
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices. An implied volatility
Implied volatility
In financial mathematics, the implied volatility of an option contract is the volatility of the price of the underlying security that is implied by the market price of the option based on an option pricing model. In other words, it is the volatility that, when used in a particular pricing model,...
is derived from the market price of a market traded derivative (in particular an option).
It is common for discussions to talk about the volatility of a security's price, even while it is the returns' volatility that is being measured. It is used to quantify the risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
of the financial instrument over the specified time period. Volatility is normally expressed in annualized terms, and it may either be an absolute number ($5) or a fraction of the mean (5%).
Volatility terminology
Volatility as described here refers to the actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days). It is the volatility of a financial instrument based on historical prices over the specified period with the last observation the most recent price. This phrase is used particularly when it is wished to distinguish between the actual current volatility of an instrument and- actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past
- actual future volatility which refers to the volatility of a financial instrument over a specified period starting at the current time and ending at a future date (normally the expiry date of an optionOption (finance)In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
) - historical implied volatility which refers to the implied volatilityImplied volatilityIn financial mathematics, the implied volatility of an option contract is the volatility of the price of the underlying security that is implied by the market price of the option based on an option pricing model. In other words, it is the volatility that, when used in a particular pricing model,...
observed from historical prices of the financial instrument (normally options) - current implied volatility which refers to the implied volatility observed from current prices of the financial instrument
- future implied volatility which refers to the implied volatility observed from future prices of the financial instrument
For a financial instrument whose price follows a Gaussian
GAUSSIAN
Gaussian is a computational chemistry software program initially released in 1970 by John Pople and his research group at Carnegie-Mellon University as Gaussian 70. It has been continuously updated since then...
random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
, or Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
, the width of the distribution increases as time increases. This is because there is an increasing probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that the instrument's price will be farther away from the initial price as time increases. However, rather than increase linearly, the volatility increases with the square-root of time as time increases, because some fluctuations are expected to cancel each other out, so the most likely deviation after twice the time will not be twice the distance from zero.
Since observed price changes do not follow Gaussian distributions, others such as the Lévy distribution are often used. These can capture attributes such as "fat tail
Fat tail
A fat-tailed distribution is a probability distribution that has the property, along with the heavy-tailed distributions, that they exhibit extremely large skewness or kurtosis. This comparison is often made relative to the ubiquitous normal distribution, which itself is an example of an...
s".
Volatility and Liquidity
Much research has been devoted to modeling and forecasting the volatility of financial returns, and yet few theoretical models explain how volatility comes to exist in the first place.Easley, López de Prado and O'Hara (2010) argue that at least one source of volatility can be explained by Market microstructure
Market microstructure
Market microstructure is a branch of finance concerned with the details of how exchange occurs in markets. While the theory of market microstructure applies to the exchange of real or financial assets, more evidence is available on the microstructure of financial markets due to the availability of...
theory, as the result of the liquidity provision process. When market makers infer the possibility of Adverse selection
Adverse selection
Adverse selection, anti-selection, or negative selection is a term used in economics, insurance, statistics, and risk management. It refers to a market process in which "bad" results occur when buyers and sellers have asymmetric information : the "bad" products or services are more likely to be...
, they adjust their trading ranges, which in turn increases the band of price oscillation. If the level of toxicity surprises market makers, they may opt to vanish from the market altogether, leading to exacerbated price moves such as the so called 2010 Flash Crash.
Volatility for investors
Investors care about volatility for five reasons. 1) The wider the swings in an investment's price the harder emotionally it is to not worry. 2) When certain cash flows from selling a security are needed at a specific future date, higher volatility means a greater chance of a shortfall. 3) Higher volatility of returns while saving for retirement results in a wider distribution of possible final portfolio values. 4) Higher volatility of return when retired gives withdrawals a larger permanent impact on the portfolio's value. 5) Price volatility presents opportunities to buy assets cheaply and sell when overpriced.In today's markets, it is also possible to trade volatility directly, through the use of derivative securities such as options
Option (finance)
In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
and variance swap
Variance swap
A variance swap is an over-the-counter financial derivative that allows one to speculate on or hedge risks associated with the magnitude of movement, i.e. volatility, of some underlying product, like an exchange rate, interest rate, or stock index....
s. See Volatility arbitrage
Volatility arbitrage
In finance, volatility arbitrage is a type of statistical arbitrage that is implemented by trading a delta neutral portfolio of an option and its underlier. The objective is to take advantage of differences between the implied volatility of the option, and a forecast of future realized volatility...
.
Volatility versus direction
Volatility does not measure the direction of price changes, merely their dispersion. This is because when calculating standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
(or variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
), all differences are squared, so that negative and positive differences are combined into one quantity. Two instruments with different volatilities may have the same expected return, but the instrument with higher volatility will have larger swings in values over a given period of time.
For example, a lower volatility stock may have an expected (average) return of 7%, with annual volatility of 5%. This would indicate returns from approximately negative 3% to positive 17% most of the time (19 times out of 20, or 95% via a two standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
rule). A higher volatility stock, with the same expected return of 7% but with annual volatility of 20%, would indicate returns from approximately negative 33% to positive 47% most of the time (19 times out of 20, or 95%). These estimates assume a normal distribution; in reality stocks are found to be leptokurtotic
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
.
Volatility over time
Although the Black Scholes equation assumes predictable constant volatility, none of these are observed in real markets, and amongst the models are Bruno DupireBruno Dupire
-Local volatility:Dupire is best known for showing how to derive a local volatility model consistent with a surface of option prices across strikes and maturities, establishing the so called Dupire's approach to local volatility for modeling the volatility smile....
's Local Volatility
Local volatility
A local volatility model, in mathematical finance and financial engineering, is one which treats volatility as a function of the current asset level S_t and of time t .-Formulation:...
, Poisson Process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
where volatility jumps to new levels with a predictable frequency, and the increasingly popular Heston model of Stochastic Volatility
Stochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
.
It's common knowledge that types of assets experience periods of high and low volatility. That is, during some periods prices go up and down quickly, while during other times they might not seem to move at all.
Periods when prices fall quickly (a crash
Stock market crash
A stock market crash is a sudden dramatic decline of stock prices across a significant cross-section of a stock market, resulting in a significant loss of paper wealth. Crashes are driven by panic as much as by underlying economic factors...
) are often followed by prices going down even more, or going up by an unusual amount. Also, a time when prices rise quickly (a bubble) may often be followed by prices going up even more, or going down by an unusual amount.
The converse behavior, 'doldrums' can last for a long time as well.
Most typically, extreme movements do not appear 'out of nowhere'; they're presaged by larger movements than usual.
This is termed autoregressive conditional heteroskedasticity
Autoregressive conditional heteroskedasticity
In econometrics, AutoRegressive Conditional Heteroskedasticity models are used to characterize and model observed time series. They are used whenever there is reason to believe that, at any point in a series, the terms will have a characteristic size, or variance...
.
Of course, whether such large movements have the same direction, or the opposite, is more difficult to say. And an increase in volatility does not always presage a further increase—the volatility may simply go back down again.
Mathematical definition
The annualized volatility σ is the standard deviation of the instrument's yearly logarithmic returns.The generalized volatility σT for time horizon T in years is expressed as:
Therefore, if the daily logarithmic returns of a stock have a standard deviation of σSD and the time period of returns is P, the annualized volatility is
A common assumption is that P = 1/252 (there are 252 trading days in any given year). Then, if σSD = 0.01 the annualized volatility is
The monthly volatility (i.e., T = 1/12 of a year) would be
The formula used above to convert returns or volatility measures from one time period to another assume a particular underlying model or process. These formulas are accurate extrapolations of a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
, or Wiener process, whose steps have finite variance. However, more generally, for natural stochastic processes, the precise relationship between volatility measures for different time periods is more complicated. Some use the Lévy stability exponent α to extrapolate natural processes:
If α = 2 you get the Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
scaling relation, but some people believe α < 2 for financial activities such as stocks, indexes and so on. This was discovered by Benoît Mandelbrot
Benoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
, who looked at cotton prices and found that they followed a Lévy alpha-stable distribution with α = 1.7. (See New Scientist, 19 April 1997.)
Crude volatility estimation
Using a simplification of the formulas above it is possible to estimate annualized volatility based solely on approximate observations. Suppose you notice that a market price index, which has a current value near 10,000, has moved about 100 points a day, on average, for many days. This would constitute a 1% daily movement, up or down.To annualize this, you can use the "rule of 16", that is, multiply by 16 to get 16% as the annual volatility. The rationale for this is that 16 is the square root of 256, which is approximately the number of trading days in a year (252). This also uses the fact that the standard deviation of the sum of n independent variables (with equal standard deviations) is √n times the standard deviation of the individual variables.
Of course, the average magnitude of the observations is merely an approximation of the standard deviation of the market index. Assuming that the market index daily changes are normally distributed with mean zero and standard deviation σ, the expected value of the magnitude of the observations
Absolute deviation
In statistics, the absolute deviation of an element of a data set is the absolute difference between that element and a given point. Typically the point from which the deviation is measured is a measure of central tendency, most often the median or sometimes the mean of the data set.D_i = |x_i-m|...
is √(2/π)σ = 0.798σ. The net effect is that this crude approach underestimates the true volatility by about 20%.
Estimate of compound annual growth rate (CAGR)
Consider the Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
:
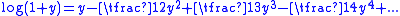
Taking only the first two terms one has:
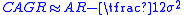
Realistically, most financial assets have negative skewness and leptokurtosis, so this formula tends to be over-optimistic. Some people use the formula:
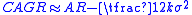
for a rough estimate, where k is an empirical factor (typically five to ten).
Criticisms
Despite their sophisticated composition, the predictive power of most volatility forecasting models is similar to that of plain-vanilla measures, such as simple past volatility. The body of work dedicated to volatility forecasting models is overwhelming. Thousands of academics have devoted their entire careers to publishing models that supposedly are able to forecast volatility. Some authors have published well over 40 papers on this very topic, and yet none seems to deliver any improvement over the simple standard deviation. Torben Andersen has fiercely attacked skeptics in a number of papers. In Answering the Critics: Yes, ARCH models do provide good volatility forecasts, Andersen and Bollerslev attack the work of leading researchers such as Cumby, Figlewski, Hasbrouck, Jorion among many others, arguing that they do not know how to correctly implement their models. In Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts, Andersen and Bollerslev again repeat their attack on those who apply Occam's RazorOccam's razor
Occam's razor, also known as Ockham's razor, and sometimes expressed in Latin as lex parsimoniae , is a principle that generally recommends from among competing hypotheses selecting the one that makes the fewest new assumptions.-Overview:The principle is often summarized as "simpler explanations...
to dismiss volatility forecasting models. It is interesting to note that while critics are publishing their papers in top journals such as Journal of Finance
Journal of Finance
The Journal of Finance is a peer-reviewed academic journal published by Wiley-Blackwell on behalf of the American Finance Association. It was established in 1946. Its current editors are Campbell R. Harvey and John R. Graham...
, Journal of Derivatives, Journal of Portfolio Management
Journal of Portfolio Management
The Journal of Portfolio Management is a quarterly academic journal covering asset allocation, performance measurement, market trends, risk management, and portfolio optimization. The journal was established in 1974 by Peter L. Bernstein. The current editor-in-chief is Frank J...
, etc. those defending their volatility forecasting models or criticizing skeptics have been unable to publish their work in journals of similar prestige, in many cases opting for leaving them unpublished, as working paper
Working paper
A working paper or work paper or workpaper may refer to:*A preliminary scientific or technical paper. Often, authors will release working papers to share ideas about a topic or to elicit feedback before submitting to a peer reviewed conference or academic journal.* Sometimes the term working paper...
s.
Besides this controversy between believers in volatility forecasting models and the large majority of skeptics, there is a contentious battle among those same believers, one claiming that his model is superior to the rest. In August 2008, Torben Andersen and Prof. Oleg Bondarenko once again surprised the academic community by claiming not only that their volatility forecasting model was superior, but that they have mathematically demonstrated that future research was futile, since no future volatility forecasting model can beat theirs.
In an interview regarding their CIV model, Andersen and Bondarenko go as far as to assert
Removed from this controversy, practitioners and portfolio managers seem to completely ignore or dismiss volatility forecasting models. For example, Nassim Taleb
Nassim Taleb
Nassim Nicholas Taleb is a Lebanese American essayist whose work focuses on problems of randomness and probability. His 2007 book The Black Swan was described in a review by Sunday Times as one of the twelve most influential books since World War II....
famously titled one of his Journal of Portfolio Management
Journal of Portfolio Management
The Journal of Portfolio Management is a quarterly academic journal covering asset allocation, performance measurement, market trends, risk management, and portfolio optimization. The journal was established in 1974 by Peter L. Bernstein. The current editor-in-chief is Frank J...
papers We Don't Quite Know What We are Talking About When We Talk About Volatility. Nassim Taleb
Nassim Taleb
Nassim Nicholas Taleb is a Lebanese American essayist whose work focuses on problems of randomness and probability. His 2007 book The Black Swan was described in a review by Sunday Times as one of the twelve most influential books since World War II....
gained worldwide recognition through his Black swan theory
Black swan theory
The black swan theory or theory of black swan events is a metaphor that encapsulates the concept that The event is a surprise and has a major impact...
, which argues the sillines of trying to predict the unpredictable.
In a similar note, Emanuel Derman
Emanuel Derman
Emanuel Derman is a South African-born academic, businessman and writer. He is best known as a quantitative analyst, and author of the book My Life as A Quant: Reflections on Physics and Finance....
expressed his disillusion with the enormous supply of empirical models unsupported by any theory. He argues that, while "theories are attempts to uncover the hidden principles underpinning the world around us, as Albert Einstein did with his theory of relativity", we should remember that "models are metaphors -- analogies that describe one thing relative to another". From that perspective, volatility forecasting models are nothing more than high-tech horoscopes: Even if they were successful predictors (which they are not), they would not add anything to our understanding of the principles governing the markets.
See also
- Beta (finance)
- Derivative (finance)Derivative (finance)A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
- Financial economicsFinancial economicsFinancial Economics is the branch of economics concerned with "the allocation and deployment of economic resources, both spatially and across time, in an uncertain environment"....
- Implied volatilityImplied volatilityIn financial mathematics, the implied volatility of an option contract is the volatility of the price of the underlying security that is implied by the market price of the option based on an option pricing model. In other words, it is the volatility that, when used in a particular pricing model,...
- IVXIVXIVX is a volatility index providing an intraday, VIX-like measure for any of US securities and exchange traded instruments. IVX is the abbreviation of Implied Volatility Index and is a popular measure of the implied volatility of each individual stock...
- RiskRiskRisk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
- Standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
- Stochastic volatilityStochastic volatilityStochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
- Volatility arbitrageVolatility arbitrageIn finance, volatility arbitrage is a type of statistical arbitrage that is implemented by trading a delta neutral portfolio of an option and its underlier. The objective is to take advantage of differences between the implied volatility of the option, and a forecast of future realized volatility...
- Volatility smileVolatility SmileIn finance, the volatility smile is a long-observed pattern in which at-the-money options tend to have lower implied volatilities than in- or out-of-the-money options. The pattern displays different characteristics for different markets and results from the probability of extreme moves...
External links
- Graphical Comparison of Implied and Historical Volatility, video
- Complex Options Multi-Leg Option Strategy Calculator
- An introduction to volatility and how it can be calculated in excel, by Dr A. A. Kotzé
- Interactive Java Applet "What is Historic Volatility?"
- Diebold, Francis X.; Hickman, Andrew; Inoue, Atsushi & Schuermannm, Til (1996) "Converting 1-Day Volatility to h-Day Volatility: Scaling by sqrt(h) is Worse than You Think"
- A short introduction to alternative mathematical concepts of volatility