
Stochastic volatility
Encyclopedia
Stochastic volatility
models are used in the field of mathematical finance
to evaluate derivative
securities, such as options
. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variable
s such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance
of the volatility process itself, among others.
Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, these models assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile
and skew, which indicate that implied volatility does tend to vary with respect to strike price
and expiry. By assuming that the volatility of the underlying price is a stochastic process rather than a constant, it becomes possible to model derivatives more accurately.
:
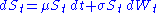
where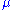 is the constant drift (i.e. expected return) of the security price
is the constant drift (i.e. expected return) of the security price  ,
,  is the constant volatility, and
is the constant volatility, and 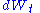 is a standard Wiener process
is a standard Wiener process
with zero mean
and unit rate of variance
. The explicit solution of this stochastic differential equation
is .
.
The Maximum likelihood estimator
to estimate the constant volatility for given stock prices
for given stock prices 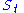 at different times
at different times 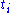 is
is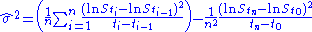 ;
;
its expectation value is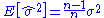 .
.
This basic model with constant volatility is the starting point for non-stochastic volatility models such as Black–Scholes and Cox–Ross–Rubinstein.
is the starting point for non-stochastic volatility models such as Black–Scholes and Cox–Ross–Rubinstein.
For a stochastic volatility model, replace the constant volatility with a function
with a function  , that models the variance of
, that models the variance of  . This variance function is also modeled as brownian motion, and the form of
. This variance function is also modeled as brownian motion, and the form of 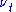 depends on the particular SV model under study.
depends on the particular SV model under study.
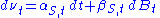
where and
and 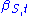 are some functions of
are some functions of  and
and  is another standard gaussian that is correlated with
is another standard gaussian that is correlated with  with constant correlation factor
with constant correlation factor 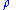 .
.
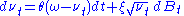
where is the mean long-term volatility,
is the mean long-term volatility, 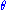 is the rate at which the volatility reverts toward its long-term mean,
is the rate at which the volatility reverts toward its long-term mean, 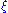 is the volatility of the volatility process, and
is the volatility of the volatility process, and 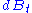 is, like
is, like 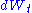 , a gaussian with zero mean and unit standard deviation. However,
, a gaussian with zero mean and unit standard deviation. However, 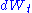 and
and 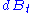 are correlated with the constant correlation
are correlated with the constant correlation
value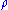 .
.
In other words, the Heston SV model assumes that the variance is a random process that
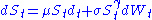
Conceptually, in some markets volatility rises when prices rise (e.g. commodities), so . In other markets, volatility tends to rise as prices fall, modelled with
. In other markets, volatility tends to rise as prices fall, modelled with  .
.
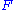 (related to any asset e.g. an index, interest rate, bond, currency or equity) under stochastic volatility
(related to any asset e.g. an index, interest rate, bond, currency or equity) under stochastic volatility  :
:
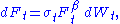
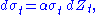
The initial values and
and 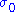 are the current forward price and volatility, whereas
are the current forward price and volatility, whereas 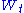 and
and 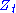 are two correlated Wiener processes (i.e. Brownian motions) with correlation coefficient
are two correlated Wiener processes (i.e. Brownian motions) with correlation coefficient 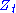 . The constant parameters
. The constant parameters 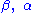 are such that
are such that 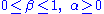 .
.
The main feature of the SABR model is to be able to reproduce the smile effect of the volatility smile
.
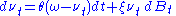
The GARCH model has been extended via numerous variants, including the NGARCH, TGARCH, IGARCH, LGARCH, EGARCH, GJR-GARCH, etc.
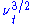 . The form of the variance differential is:
. The form of the variance differential is:
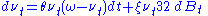 .
.
However the meaning of the parameters is different from Heston model. In this model both, mean reverting and volatility of variance parameters, are stochastic quantities given by and
and 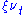 respectively.
respectively.
.
Specifically, the dynamics of the instantaneous interest rate are given by following the stochastic differential equations:
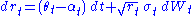 ,
, ,
,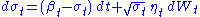 .
.
(MLE). For instance, in the Heston model, the set of model parameters can be estimated applying an MLE algorithm such as the Powell Directed Set
can be estimated applying an MLE algorithm such as the Powell Directed Set
method http://www.library.cornell.edu/nr/bookcpdf.html to observations of historic underlying security prices.
In this case, you start with an estimate for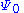 , compute the residual errors when applying the historic price data to the resulting model, and then adjust
, compute the residual errors when applying the historic price data to the resulting model, and then adjust 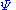 to try to minimize these errors. Once the calibration has been performed, it is standard practice to re-calibrate the model over time.
to try to minimize these errors. Once the calibration has been performed, it is standard practice to re-calibrate the model over time.
Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
models are used in the field of mathematical finance
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
to evaluate derivative
Derivative (finance)
A derivative instrument is a contract between two parties that specifies conditions—in particular, dates and the resulting values of the underlying variables—under which payments, or payoffs, are to be made between the parties.Under U.S...
securities, such as options
Option (finance)
In finance, an option is a derivative financial instrument that specifies a contract between two parties for a future transaction on an asset at a reference price. The buyer of the option gains the right, but not the obligation, to engage in that transaction, while the seller incurs the...
. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variable
State variable
A state variable is one of the set of variables that describe the "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour...
s such as the price level of the underlying security, the tendency of volatility to revert to some long-run mean value, and the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the volatility process itself, among others.
Stochastic volatility models are one approach to resolve a shortcoming of the Black–Scholes model. In particular, these models assume that the underlying volatility is constant over the life of the derivative, and unaffected by the changes in the price level of the underlying security. However, these models cannot explain long-observed features of the implied volatility surface such as volatility smile
Volatility Smile
In finance, the volatility smile is a long-observed pattern in which at-the-money options tend to have lower implied volatilities than in- or out-of-the-money options. The pattern displays different characteristics for different markets and results from the probability of extreme moves...
and skew, which indicate that implied volatility does tend to vary with respect to strike price
Strike price
In options, the strike price is a key variable in a derivatives contract between two parties. Where the contract requires delivery of the underlying instrument, the trade will be at the strike price, regardless of the spot price of the underlying instrument at that time.Formally, the strike...
and expiry. By assuming that the volatility of the underlying price is a stochastic process rather than a constant, it becomes possible to model derivatives more accurately.
Basic model
Starting from a constant volatility approach, assume that the derivative's underlying price follows a standard model for geometric brownian motionGeometric Brownian motion
A geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
:
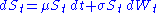
where
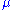 is the constant drift (i.e. expected return) of the security price
is the constant drift (i.e. expected return) of the security price  ,
,  is the constant volatility, and
is the constant volatility, and 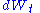 is a standard Wiener process
is a standard Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
with zero mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and unit rate of variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
. The explicit solution of this stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
is
 .
.The Maximum likelihood estimator
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
to estimate the constant volatility
 for given stock prices
for given stock prices 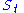 at different times
at different times 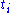 is
is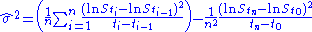 ;
;its expectation value is
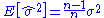 .
.This basic model with constant volatility
 is the starting point for non-stochastic volatility models such as Black–Scholes and Cox–Ross–Rubinstein.
is the starting point for non-stochastic volatility models such as Black–Scholes and Cox–Ross–Rubinstein.For a stochastic volatility model, replace the constant volatility
 with a function
with a function 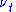 , that models the variance of
, that models the variance of  . This variance function is also modeled as brownian motion, and the form of
. This variance function is also modeled as brownian motion, and the form of 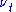 depends on the particular SV model under study.
depends on the particular SV model under study.
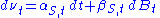
where
 and
and 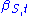 are some functions of
are some functions of  and
and  is another standard gaussian that is correlated with
is another standard gaussian that is correlated with  with constant correlation factor
with constant correlation factor 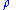 .
.Heston model
The popular Heston model is a commonly used SV model, in which the randomness of the variance process varies as the square root of variance. In this case, the differential equation for variance takes the form: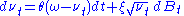
where
 is the mean long-term volatility,
is the mean long-term volatility, 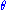 is the rate at which the volatility reverts toward its long-term mean,
is the rate at which the volatility reverts toward its long-term mean, 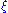 is the volatility of the volatility process, and
is the volatility of the volatility process, and 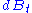 is, like
is, like 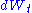 , a gaussian with zero mean and unit standard deviation. However,
, a gaussian with zero mean and unit standard deviation. However, 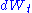 and
and 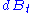 are correlated with the constant correlation
are correlated with the constant correlationCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
value
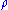 .
.In other words, the Heston SV model assumes that the variance is a random process that
- exhibits a tendency to revert towards a long-term mean
 at a rate
at a rate 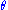 ,
, - exhibits a volatility proportional to the square root of its level
- and whose source of randomness is correlated (with correlation
 ) with the randomness of the underlying's price processes.
) with the randomness of the underlying's price processes.
CEV Model
The CEV model describes the relationship between volatility and price, introducing stochastic volatility: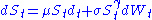
Conceptually, in some markets volatility rises when prices rise (e.g. commodities), so
 . In other markets, volatility tends to rise as prices fall, modelled with
. In other markets, volatility tends to rise as prices fall, modelled with  .
.SABR volatility model
The SABR model (Stochastic Alpha, Beta, Rho) describes a single forward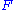 (related to any asset e.g. an index, interest rate, bond, currency or equity) under stochastic volatility
(related to any asset e.g. an index, interest rate, bond, currency or equity) under stochastic volatility  :
: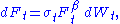
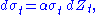
The initial values
 and
and 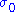 are the current forward price and volatility, whereas
are the current forward price and volatility, whereas 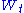 and
and 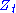 are two correlated Wiener processes (i.e. Brownian motions) with correlation coefficient
are two correlated Wiener processes (i.e. Brownian motions) with correlation coefficient 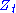 . The constant parameters
. The constant parameters 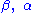 are such that
are such that 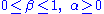 .
.The main feature of the SABR model is to be able to reproduce the smile effect of the volatility smile
Volatility Smile
In finance, the volatility smile is a long-observed pattern in which at-the-money options tend to have lower implied volatilities than in- or out-of-the-money options. The pattern displays different characteristics for different markets and results from the probability of extreme moves...
.
GARCH model
The Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model is another popular model for estimating stochastic volatility. It assumes that the randomness of the variance process varies with the variance, as opposed to the square root of the variance as in the Heston model. The standard GARCH(1,1) model has the following form for the variance differential: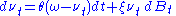
The GARCH model has been extended via numerous variants, including the NGARCH, TGARCH, IGARCH, LGARCH, EGARCH, GJR-GARCH, etc.
3/2 model
The 3/2 model is similar to the Heston model, but assumes that the randomness of the variance process varies with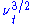 . The form of the variance differential is:
. The form of the variance differential is: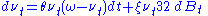 .
.However the meaning of the parameters is different from Heston model. In this model both, mean reverting and volatility of variance parameters, are stochastic quantities given by
 and
and 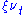 respectively.
respectively.Chen model
In interest rate modelings, Lin Chen in 1994 developed the first stochastic mean and stochastic volatility model, Chen modelChen model
In finance, the Chen model is a mathematical model describing the evolution of interest rates. It is a type of "three-factor model" as it describes interest rate movements as driven by three sources of market risk...
.
Specifically, the dynamics of the instantaneous interest rate are given by following the stochastic differential equations:
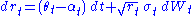 ,
, ,
,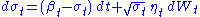 .
.Calibration
Once a particular SV model is chosen, it must be calibrated against existing market data. Calibration is the process of identifying the set of model parameters that are most likely given the observed data. This process is called Maximum Likelihood EstimationMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
(MLE). For instance, in the Heston model, the set of model parameters
 can be estimated applying an MLE algorithm such as the Powell Directed Set
can be estimated applying an MLE algorithm such as the Powell Directed SetDirected set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
method http://www.library.cornell.edu/nr/bookcpdf.html to observations of historic underlying security prices.
In this case, you start with an estimate for
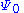 , compute the residual errors when applying the historic price data to the resulting model, and then adjust
, compute the residual errors when applying the historic price data to the resulting model, and then adjust 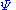 to try to minimize these errors. Once the calibration has been performed, it is standard practice to re-calibrate the model over time.
to try to minimize these errors. Once the calibration has been performed, it is standard practice to re-calibrate the model over time.See also
- Chen modelChen modelIn finance, the Chen model is a mathematical model describing the evolution of interest rates. It is a type of "three-factor model" as it describes interest rate movements as driven by three sources of market risk...
- Heston modelHeston modelIn finance, the Heston model, named after Steven Heston, is a mathematical model describing the evolution of the volatility of an underlying asset...
- Local volatilityLocal volatilityA local volatility model, in mathematical finance and financial engineering, is one which treats volatility as a function of the current asset level S_t and of time t .-Formulation:...
- Risk-neutral measureRisk-neutral measureIn mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
- SABR Volatility ModelSABR Volatility ModelIn mathematical finance, the SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "Stochastic Alpha, Beta, Rho", referring to the parameters of the model. The SABR model is widely used by practitioners in the...
- VolatilityVolatility (finance)In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
- Volatility, uncertainty, complexity and ambiguity
- Black–Scholes

