
Heston model
Encyclopedia
In finance, the Heston model, named after Steven Heston, is a mathematical model
describing the evolution of the volatility
of an underlying
asset. It is a stochastic volatility
model: such a model assumes that the volatility of the asset is not constant, nor even deterministic, but follows a random process.

where , the instantaneous variance, is a CIR process
, the instantaneous variance, is a CIR process
:
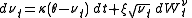
and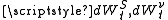 are Wiener process
are Wiener process
es (i.e., random walks) with correlation ρ.
The parameters in the above equations represent the following:
If the parameters obey the following condition (known as the Feller condition) then the process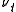 is strictly positive
is strictly positive 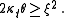
A first straightforward extension is to allow the parameters to be time-dependent. The model dynamics are then written as:
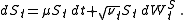
Here , the instantaneous variance, is a time-dependent CIR process
, the instantaneous variance, is a time-dependent CIR process
:
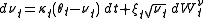
and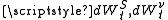 are Wiener process
are Wiener process
es (i.e., random walks) with correlation ρ. In order to retain model tractability, one may require parameters to be piecewise-constant.
Another approach is to add a second process of variance, independent of the first one.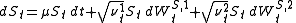
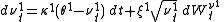
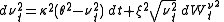
A significant extension of Heston model to make both volatility and mean stochastic is given by Lin Chen (1996). In the Chen model
the dynamics of the instantaneous interest rate are specified by
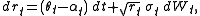

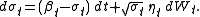
A fundamental concept in derivatives pricing is that of the Risk-neutral measure
; this is explained in further depth in the above article. For our purposes, it is sufficient to note the following:
Consider a general situation where we have underlying assets and a linearly independent set of
underlying assets and a linearly independent set of 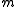 Wiener processes. The set of equivalent measures is isomorphic to Rm, the space of possible drifts. Let us consider the set of equivalent martingale measures to be isomorphic to a manifold
Wiener processes. The set of equivalent measures is isomorphic to Rm, the space of possible drifts. Let us consider the set of equivalent martingale measures to be isomorphic to a manifold 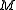 embedded in Rm; initially, consider the situation where we have no assets and
embedded in Rm; initially, consider the situation where we have no assets and 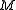 is isomorphic to Rm.
is isomorphic to Rm.
Now let us consider each of the underlying assets as providing a constraint on the set of equivalent measures, as its expected discount process must be equal to a constant (namely, its initial value). By adding one asset at a time, we may consider each additional constraint as reducing the dimension of by one dimension. Hence we can see that in the general situation described above, the dimension of the set of equivalent martingale measures is
by one dimension. Hence we can see that in the general situation described above, the dimension of the set of equivalent martingale measures is  .
.
In the Black-Scholes model, we have one asset and one Wiener process. The dimension of the set of equivalent martingale measures is zero; hence it can be shown that there is a single value for the drift, and thus a single risk-neutral measure, under which the discounted asset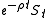 will be a martingale.
will be a martingale.
In the Heston model, we still have one asset (volatility is not considered to be directly observable or tradeable in the market) but we now have two Wiener processes - the first in the Stochastic Differential Equation (SDE) for the asset and the second in the SDE for the stochastic volatility. Here, the dimension of the set of equivalent martingale measures is one; there is no unique risk-free measure.
This is of course problematic; while any of the risk-free measures may theoretically be used to price a derivative, it is likely that each of them will give a different price. In theory, however, only one of these risk-free measures would be compatible with the market prices of volatility-dependent options (for example, European calls, or more explicitly, variance swap
s). Hence we could add a volatility-dependent asset; by doing so, we add an additional constraint, and thus choose a single risk-free measure which is compatible with the market. This measure may be used for pricing.
.
Information about how to use the Fourier transform to value options is given in a paper by Carr and Madan
.
Extension of the Heston model with stochastic interest rates is given in the paper by Grzelak and Oosterlee
.
Derivation of closed-form option prices for time-dependent Heston model is presented in the paper by Benhamou et al
.
Derivation of closed-form option prices for double Heston model are presented in papers by Christoffersen
and also Gauthier.
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
describing the evolution of the volatility
Volatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
of an underlying
Underlying
In finance, the underlying of a derivative is an asset, basket of assets, index, or even another derivative, such that the cash flows of the derivative depend on the value of this underlying...
asset. It is a stochastic volatility
Stochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
model: such a model assumes that the volatility of the asset is not constant, nor even deterministic, but follows a random process.
Basic Heston model
The basic Heston model assumes that St, the price of the asset, is determined by a stochastic process:
where
 , the instantaneous variance, is a CIR process
, the instantaneous variance, is a CIR processCIR process
The CIR process is a Markov process with continuous paths defined by the following stochastic differential equation :dr_t = \theta \,dt + \sigma\, \sqrt r_t dW_t\,...
:
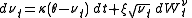
and
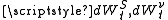 are Wiener process
are Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
es (i.e., random walks) with correlation ρ.
The parameters in the above equations represent the following:
- μ is the rate of return of the asset.
- θ is the long variance, or long run average price variance; as t tends to infinity, the expected value of νt tends to θ.
- κ is the rate at which νt reverts to θ.
- ξ is the vol of vol, or volatility of the volatility; as the name suggests, this determines the variance of νt.
If the parameters obey the following condition (known as the Feller condition) then the process
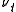 is strictly positive
is strictly positive 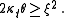
Extensions
In order to take into account all the features from the volatility surface, the Heston model may be a too rigid framework. It may be necessary to add degrees of freedom to the original model.A first straightforward extension is to allow the parameters to be time-dependent. The model dynamics are then written as:
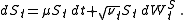
Here
 , the instantaneous variance, is a time-dependent CIR process
, the instantaneous variance, is a time-dependent CIR processCIR process
The CIR process is a Markov process with continuous paths defined by the following stochastic differential equation :dr_t = \theta \,dt + \sigma\, \sqrt r_t dW_t\,...
:
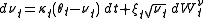
and
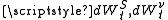 are Wiener process
are Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
es (i.e., random walks) with correlation ρ. In order to retain model tractability, one may require parameters to be piecewise-constant.
Another approach is to add a second process of variance, independent of the first one.
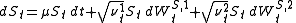
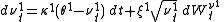
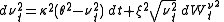
A significant extension of Heston model to make both volatility and mean stochastic is given by Lin Chen (1996). In the Chen model
Chen model
In finance, the Chen model is a mathematical model describing the evolution of interest rates. It is a type of "three-factor model" as it describes interest rate movements as driven by three sources of market risk...
the dynamics of the instantaneous interest rate are specified by
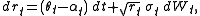

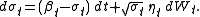
Risk-neutral measure
- See Risk-neutral measureRisk-neutral measureIn mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
for the complete article
A fundamental concept in derivatives pricing is that of the Risk-neutral measure
Risk-neutral measure
In mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
; this is explained in further depth in the above article. For our purposes, it is sufficient to note the following:
- To price a derivative whose payoff is a function of one or more underlying assets, we evaluate the expected value of its discounted payoff under a risk-neutral measure.
- A risk-neutral measure, also known as an equivalent martingale measure, is one which is equivalent to the real-world measure, and which is arbitrage-free: under such a measure, the discounted prices of each of the underlying assets is a martingale. See Girsanov's theorem.
- In the Black-Scholes and Heston frameworks (where filtrations are generated from a linearly independent set of Wiener processes alone), any equivalent measure can be described in a very loose sense by adding a drift to each of the Wiener processes.
- By selecting certain values for the drifts described above, we may obtain an equivalent measure which fulfills the arbitrage-free condition.
Consider a general situation where we have
 underlying assets and a linearly independent set of
underlying assets and a linearly independent set of 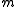 Wiener processes. The set of equivalent measures is isomorphic to Rm, the space of possible drifts. Let us consider the set of equivalent martingale measures to be isomorphic to a manifold
Wiener processes. The set of equivalent measures is isomorphic to Rm, the space of possible drifts. Let us consider the set of equivalent martingale measures to be isomorphic to a manifold 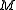 embedded in Rm; initially, consider the situation where we have no assets and
embedded in Rm; initially, consider the situation where we have no assets and 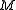 is isomorphic to Rm.
is isomorphic to Rm.Now let us consider each of the underlying assets as providing a constraint on the set of equivalent measures, as its expected discount process must be equal to a constant (namely, its initial value). By adding one asset at a time, we may consider each additional constraint as reducing the dimension of
 by one dimension. Hence we can see that in the general situation described above, the dimension of the set of equivalent martingale measures is
by one dimension. Hence we can see that in the general situation described above, the dimension of the set of equivalent martingale measures is  .
.In the Black-Scholes model, we have one asset and one Wiener process. The dimension of the set of equivalent martingale measures is zero; hence it can be shown that there is a single value for the drift, and thus a single risk-neutral measure, under which the discounted asset
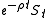 will be a martingale.
will be a martingale.In the Heston model, we still have one asset (volatility is not considered to be directly observable or tradeable in the market) but we now have two Wiener processes - the first in the Stochastic Differential Equation (SDE) for the asset and the second in the SDE for the stochastic volatility. Here, the dimension of the set of equivalent martingale measures is one; there is no unique risk-free measure.
This is of course problematic; while any of the risk-free measures may theoretically be used to price a derivative, it is likely that each of them will give a different price. In theory, however, only one of these risk-free measures would be compatible with the market prices of volatility-dependent options (for example, European calls, or more explicitly, variance swap
Variance swap
A variance swap is an over-the-counter financial derivative that allows one to speculate on or hedge risks associated with the magnitude of movement, i.e. volatility, of some underlying product, like an exchange rate, interest rate, or stock index....
s). Hence we could add a volatility-dependent asset; by doing so, we add an additional constraint, and thus choose a single risk-free measure which is compatible with the market. This measure may be used for pricing.
Implementation
A recent discussion of implementation of the Heston model is given in a paper by Kahl and Jäckel.
Information about how to use the Fourier transform to value options is given in a paper by Carr and Madan
.
Extension of the Heston model with stochastic interest rates is given in the paper by Grzelak and Oosterlee
.
Derivation of closed-form option prices for time-dependent Heston model is presented in the paper by Benhamou et al
.
Derivation of closed-form option prices for double Heston model are presented in papers by Christoffersen
and also Gauthier.
See also
- Stochastic volatilityStochastic volatilityStochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
- Risk-neutral measureRisk-neutral measureIn mathematical finance, a risk-neutral measure, is a prototypical case of an equivalent martingale measure. It is heavily used in the pricing of financial derivatives due to the fundamental theorem of asset pricing, which implies that in a complete market a derivative's price is the discounted...
(another name for the equivalent martingale measure) - Girsanov's theorem
- Martingale (probability theory)Martingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
- SABR Volatility ModelSABR Volatility ModelIn mathematical finance, the SABR model is a stochastic volatility model, which attempts to capture the volatility smile in derivatives markets. The name stands for "Stochastic Alpha, Beta, Rho", referring to the parameters of the model. The SABR model is widely used by practitioners in the...

