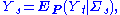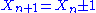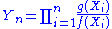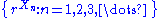Martingale (probability theory) - AbsoluteAstronomy.com

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

of random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

s (i.e., a stochastic process

Stochastic process

In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

) for which, at a particular time in the realized

Realization (probability)

In probability and statistics, a realization, or observed value, of a random variable is the value that is actually observed . The random variable itself should be thought of as the process how the observation comes about...

sequence, the expectation

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

of the next value in the sequence is equal to the present observed value even given knowledge of all prior observed value

Realization (probability)

s at a current time.

To contrast, in a process that is not a martingale, it may still be the case that the expected value of the process at one time is equal to the expected value of the process at the next time. However, knowledge of the prior outcomes (e.g., all prior cards drawn from a card deck) may be able to reduce the uncertainty of future outcomes. Thus, the expected value of the next outcome given knowledge of the present and all prior outcomes may be higher than the current outcome if a winning strategy is used. Martingales exclude the possibility of winning strategies based on game history, and thus they are a model of fair games.

History

Originally, martingale
Martingale (betting system)
Originally, martingale referred to a class of betting strategies popular in 18th century France. The simplest of these strategies was designed for a game in which the gambler wins his stake if a coin comes up heads and loses it if the coin comes up tails...

referred to a class of betting strategies

Betting strategy

A betting strategy or betting system is a structured approach to gambling intended to counter the inherent bias held by the house in casino and card games, by bookmakers in horseracing and sports betting, and other gambling situations...

that was popular in 18th century France

France

The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...

. The simplest of these strategies was designed for a game in which the gambler wins his stake if a coin comes up heads and loses it if the coin comes up tails. The strategy had the gambler double his bet after every loss so that the first win would recover all previous losses plus win a profit equal to the original stake. As the gambler's wealth and available time jointly approach infinity, his probability of eventually flipping heads approaches 1, which makes the martingale betting strategy seem like a sure thing

Almost surely

In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...

. However, the exponential growth

Exponential growth

Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...

of the bets eventually bankrupts its users. Stopped Brownian motion, which is a martingale process, can be used to model the trajectory of such games.

The concept of martingale in probability theory was introduced by Paul Pierre Lévy

Paul Pierre Lévy

Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...

, and much of the original development of the theory was done by Joseph Leo Doob

Joseph Leo Doob

Joseph Leo Doob was an American mathematician, specializing in analysis and probability theory.The theory of martingales was developed by Doob.-Early life and education:...

among others. Part of the motivation for that work was to show the impossibility of successful betting strategies.

Definitions

A basic definition of a discrete-time martingale is a discrete-time stochastic process

Stochastic process

In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

(i.e., a sequence

Sequence

of random variable

Random variable

s) X₁, X₂, X₃, ... that satisfies for any time n,

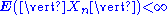
That is, the conditional expected value of the next observation, given all the past observations, is equal to the last observation. Due to the linearity of expectation, this second requirement is equivalent to:

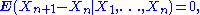
which states that the average "winnings" from observation

to observation

are 0.

Martingale Sequences with Respect to Another Sequence

More generally, a sequence Y₁, Y₂, Y₃ ... is said to be a martingale with respect to another sequence X₁, X₂, X₃ ... if for all n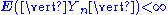

Similarly, a continuous-time martingale with respect to the stochastic process

Stochastic process

In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

X_t is a stochastic process

Stochastic process

In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...

Y_t such that for all t

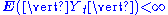
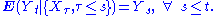
This expresses the property that the conditional expectation of an observation at time t, given all the observations up to time

, is equal to the observation at time s (of course, provided that s ≤ t).

General Definition

In full generality, a stochastic process Y : T × Ω → S is a martingale with respect to a filtration Σ_∗ and probability measure P if

Σ_∗ is a filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...

of the underlying probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...

(Ω, Σ, P);
Y is adapted
Adapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...

to the filtration Σ_∗, i.e., for each t in the index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...

T, the random variable Y_t is a Σ_t-measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

;
for each t, Y_t lies in the L^p space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

L¹(Ω, Σ_t, P; S), i.e.

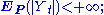
for all s and t with s < t and all F ∈ Σ_s,

where χ_F denotes the indicator function of the event F. In Grimmett and Stirzaker's Probability and Random Processes, this last condition is denoted as

which is a general form of conditional expectation

Conditional expectation

In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....

It is important to note that the property of being a martingale involves both the filtration and the probability measure (with respect to which the expectations are taken). It is possible that Y could be a martingale with respect to one measure but not another one; the Girsanov theorem

Girsanov theorem

In probability theory, the Girsanov theorem describes how the dynamics of stochastic processes change when the original measure is changed to an equivalent probability measure...

offers a way to find a measure with respect to which an Itō process is a martingale.

Examples of martingales

An unbiased random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...

(in any number of dimensions) is an example of a martingale.

A gambler's fortune (capital) is a martingale if all the betting games which the gambler plays are fair.

Polya's urn contains a number of different coloured marbles, and each iteration
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...

a marble is randomly selected out of the urn and replaced with several more of that same colour. For any given colour, the ratio of marbles inside the urn with that colour is a martingale. For example, if currently 95% of the marbles are red then, although the next iteration is much more likely than not to cause more red marbles to be added, this bias is exactly balanced out by the fact that adding more red marbles would alter the ratio much less significantly than adding the same number of non-red marbles would.

Suppose X_n is a gambler's fortune after n tosses of a fair coin
Fair coin
In probability theory and statistics, a sequence of independent Bernoulli trials with probability 1/2 of success on each trial is metaphorically called a fair coin. One for which the probability is not 1/2 is called a biased or unfair coin...

, where the gambler wins $1 if the coin comes up heads and loses $1 if the coin comes up tails. The gambler's conditional expected fortune after the next trial, given the history, is equal to his present fortune, so this sequence is a martingale.

Let Y_n = X_n² − n where X_n is the gambler's fortune from the preceding example. Then the sequence { Y_n : n = 1, 2, 3, ... } is a martingale. This can be used to show that the gambler's total gain or loss varies roughly between plus or minus the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

of the number of steps.

(de Moivre
Abraham de Moivre
Abraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...

's martingale) Now suppose an "unfair" or "biased" coin, with probability p of "heads" and probability q = 1 − p of "tails". Let

with "+" in case of "heads" and "−" in case of "tails". Let

Then { Y_n : n = 1, 2, 3, ... } is a martingale with respect to { X_n : n = 1, 2, 3, ... }. To show this

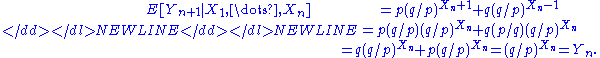
(Likelihood-ratio test
Likelihood-ratio test
In statistics, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which is a special case of the other . The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other...

ing in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

) A population is thought to be distributed according to either a probability density f or another probability density g. A random sample
Random sample
In statistics, a sample is a subject chosen from a population for investigation; a random sample is one chosen by a method involving an unpredictable component...

is taken, the data being X₁, ..., X_n. Let Y_n be the "likelihood ratio"

. If the population is actually distributed according to the density f rather than according to g, then { Y_n : n = 1, 2, 3, ... } is a martingale with respect to { X_n : n = 1, 2, 3, ... }.

Suppose each amoeba
Amoeba
Amoeba is a genus of Protozoa.History=The amoeba was first discovered by August Johann Rösel von Rosenhof in 1757. Early naturalists referred to Amoeba as the Proteus animalcule after the Greek god Proteus, who could change his shape...

either splits into two amoebas, with probability p, or eventually dies, with probability 1 − p. Let X_n be the number of amoebas surviving in the nth generation (in particular X_n = 0 if the population has become extinct by that time). Let r be the probability of eventual extinction. (Finding r as function of p is an instructive exercise. Hint: The probability that the descendants of an amoeba eventually die out is equal to the probability that either of its immediate offspring dies out, given that the original amoeba has split.) Then

is a martingale with respect to { X_n: n = 1, 2, 3, ... }.

The number of individuals of any particular species in an ecosystem of fixed size is a function of (discrete) time, and may be viewed as a sequence of random variables. This sequence is a martingale under the unified neutral theory of biodiversity
Unified neutral theory of biodiversity
The unified neutral theory of biodiversity and biogeography is a hypothesis and the title of a monograph by ecologist Stephen Hubbell...

.

If { N_t : t ≥ 0 } is a Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...

with intensity λ, then the Compensated Poisson process { N_t − λt : t ≥ 0 } is a continuous-time martingale with right-continuous/left-limit
Classification of discontinuities
Continuous functions are of utmost importance in mathematics and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there...

sample paths.

An example martingale series can easily be produced with computer software:
Microsoft Excel
Microsoft Excel
Microsoft Excel is a proprietary commercial spreadsheet application written and distributed by Microsoft for Microsoft Windows and Mac OS X. It features calculation, graphing tools, pivot tables, and a macro programming language called Visual Basic for Applications...

or similar spreadsheet software. Enter 0.0 in the A1 (top left) cell, and in the cell below it (A2) enter =A1+NORMINV(RAND,0,1). Now copy that cell by dragging down to create 300 or so copies. This will create a martingale series with a mean of 0 and standard deviation of 1. With the cells still highlighted go to the chart creation tool and create a chart of these values. Now every time a recalculation happens (in Excel the F9 key does this) the chart will display another martingale series.
R. To recreate the example above, issue plot(cumsum(rnorm(100, mean=0, sd=1)), t="l", col="darkblue", lwd=3). To display another martingale series, reissue the command.

Submartingales, supermartingales, and relationship to harmonic functions

There are two popular generalizations of a martingale that also include cases when the current observation X_n is not necessarily equal to the future conditional expectation E[X_n+1|X₁,...,X_n] but instead an upper or lower bound on the conditional expectation. These definitions reflect a relationship between martingale theory and potential theory

Potential theory

In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...

, which is the study of harmonic function

Harmonic function

In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....

s. Just as a continuous-time martingale satisfies E[X_t|{X_τ : τ≤s}] − X_s = 0 ∀s ≤ t, a harmonic function f satisfies the partial

Stochastic partial differential equation

Stochastic partial differential equations are similar to ordinary stochastic differential equations. They are essentially partial differential equations that have additional random terms. They can be exceedingly difficult to solve...

stochastic differential equation

Stochastic differential equation

A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....

Δf = 0 where Δ is the Laplacian operator

Laplace operator

In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...

. Given a Brownian motion

Brownian motion

Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...

process W_t and a harmonic function f, the resulting process f(W_t) will also be a martingale.

A discrete-time submartingale is a sequence 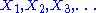of integrable random variables satisfying

Likewise, a continuous-time submartingale will satisfy

In potential theory, a subharmonic function

Subharmonic function

In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....

f will satisfy Δf ≥ 0. Any subharmonic function that is bounded above by a harmonic function for all points on the boundary of a ball will be bounded above by the harmonic function for all points inside the ball. Similarly, if a submartingale and a martingale have equivalent expectations for a given time, the history of the submartingale will tend to be bounded above by the history of the martingale. Roughly speaking, the prefix

Prefix

A prefix is an affix which is placed before the root of a word. Particularly in the study of languages,a prefix is also called a preformative, because it alters the form of the words to which it is affixed.Examples of prefixes:...

"sub-" is consistent because the current observation X_n is less than (or equal to) the conditional expectation E[X_n+1|X₁,...,X_n]. Consequently, the current observation provides support from below the future conditional expectation, and the process tends to increase in future time.

Analogously, a discrete-time supermartingale satisfies

Likewise, a continuous-time supermartingale will satisfy

In potential theory, a superharmonic function f will satisfy Δf ≤ 0. Any superharmonic function that is bounded below by a harmonic function for all points on the boundary of a ball will be bounded below by the harmonic function for all points inside the ball. Similarly, if a supermartingale and a martingale have equivalent expectations for a given time, the history of the supermartingale will tend to be bounded below by the history of the martingale. Roughly speaking, the prefix "super-" is consistent because the current observation X_n is greater than (or equal to) the conditional expectation E[X_n+1|X₁,...,X_n]. Consequently, the current observation provides support from above the future conditional expectation, and the process tends to decrease in future time.

Methods for remembering the difference between super- and submartingale

"Life is a supermartingale; as time advances, expectation decreases."
The "b" in "submartingale" points up, which is consistent with the upward expectation in a submartingale. Similarly, the "p" in "supermartingale" points downward, which is consistent with the downward expectation in a supermartingale.
The "super" and "sub" refer to the current observation and not the future expectation. Thus, a "submartingale" is a process for which the current observation (X_n) is lower than the future conditional expectation (E[X_n+1|X₁,...,X_n]). Likewise, a "supermartingale" is a process for which the current observation (X_n) is higher than the future conditional expectation (E[X_n+1|X₁,...,X_n]). A submartingale rises because it is supported from below; a supermartingale falls because it is supported from above.

Examples of submartingales and supermartingales

Every martingale is also a submartingale and a supermartingale. Conversely, any stochastic process that is both a submartingale and a supermartingale is a martingale.
Consider again the gambler who wins $1 when a coin comes up heads and loses $1 when the coin comes up tails. Suppose now that the coin may be biased, so that it comes up heads with probability p.
- If p is equal to 1/2, the gambler on average neither wins nor loses money, and the gambler's fortune over time is a martingale.
- If p is less than 1/2, the gambler loses money on average, and the gambler's fortune over time is a supermartingale.
- If p is greater than 1/2, the gambler wins money on average, and the gambler's fortune over time is a submartingale.
A convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

of a martingale is a submartingale, by Jensen's inequality
Jensen's inequality
In mathematics, Jensen's inequality, named after the Danish mathematician Johan Jensen, relates the value of a convex function of an integral to the integral of the convex function. It was proved by Jensen in 1906. Given its generality, the inequality appears in many forms depending on the context,...

. For example, the square of the gambler's fortune in the fair coin game is a submartingale (which also follows from the fact that X_n² − n is a martingale). Similarly, a concave function
Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...

of a martingale is a supermartingale.

Martingales and stopping times

A stopping time with respect to a sequence of random variables X₁, X₂, X₃, ... is a random variable τ with the property that for each t, the occurrence or non-occurrence of the event τ = t depends only on the values of X₁, X₂, X₃, ..., X_t. The intuition behind the definition is that at any particular time t, you can look at the sequence so far and tell if it is time to stop. An example in real life might be the time at which a gambler leaves the gambling table, which might be a function of his previous winnings (for example, he might leave only when he goes broke), but he can't choose to go or stay based on the outcome of games that haven't been played yet.

In some contexts the concept of stopping time is defined by requiring only that the occurrence or non-occurrence of the event τ = t be probabilistically independent

Statistical independence

In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...

of X_t + 1, X_t + 2, ... but not that it be completely determined by the history of the process up to time t. That is a weaker condition than the one appearing in the paragraph above, but is strong enough to serve in some of the proofs in which stopping times are used.

One of the basic properties of martingales is that, if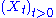

is a (sub-/super-) martingale and

is a stopping time, then the corresponding stopped process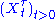

defined by

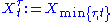is also a (sub-/super-) martingale.

The concept of a stopped martingale leads to a series of important theorems, including, for example, the optional stopping theorem

Optional stopping theorem

In probability theory, the optional stopping theorem says that, under certain conditions, the expected value of a martingale at a stopping time is equal to its initial value...

which states that, under certain conditions, the expected value of a martingale at a stopping time is equal to its initial value. We can use it, for example, to prove the impossibility of successful betting strategies for a gambler with a finite lifetime and a house limit on bets.

History

Definitions

Martingale Sequences with Respect to Another Sequence

General Definition

Examples of martingales

Submartingales, supermartingales, and relationship to harmonic functions

Methods for remembering the difference between super- and submartingale

Examples of submartingales and supermartingales

Martingales and stopping times

See also