Classification of discontinuities
Encyclopedia
Continuous function
s are of utmost importance in mathematics
and applications. However, not all functions
are continuous. If a function is not continuous at a point in its domain
, one says that it has a discontinuity there. The set of all points of discontinuity of a function may be a discrete set, a dense set
, or even the entire domain of the function.
This article describes the classification of discontinuities in the simplest case of functions of a single real
variable taking real values.
The term removable discontinuity is sometimes incorrectly used for cases in which the limits in both directions exist and are equal, while the function is undefined at the point This use is improper because continuity
This use is improper because continuity
and discontinuity of a function are concepts defined only for points in the function's domain. Such a point not in the domain, is properly named a removable singularity.
The oscillation
of a function at a point quantifies these discontinuities as follows:
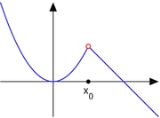
 1. Consider the function
1. Consider the function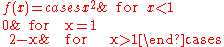
Then, the point is a removable discontinuity.
is a removable discontinuity.
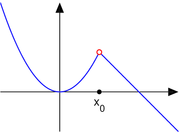
 2. Consider the function
2. Consider the function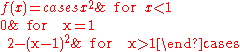
Then, the point is a jump discontinuity.
is a jump discontinuity.
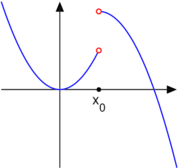
 3. Consider the function
3. Consider the function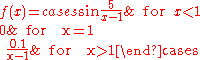
Then, the point is an essential discontinuity (sometimes called infinite discontinuity). For it to be an essential discontinuity, it would have sufficed that only one of the two one-sided limits did not exist or were infinite. However, given this example the discontinuity is also an essential discontinuity for the extension of the function into complex variables.
is an essential discontinuity (sometimes called infinite discontinuity). For it to be an essential discontinuity, it would have sufficed that only one of the two one-sided limits did not exist or were infinite. However, given this example the discontinuity is also an essential discontinuity for the extension of the function into complex variables.
. The set of discontinuities is an Fσ set
.
The set of discontinuities of a monotonic function
is at most countable. This is Froda's theorem
.
Thomae's function is discontinuous at every rational point, but continuous at every irrational point.
The indicator function of the rationals, also known as the Dirichlet function, is discontinuous everywhere
.
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s are of utmost importance in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and applications. However, not all functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
are continuous. If a function is not continuous at a point in its domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
, one says that it has a discontinuity there. The set of all points of discontinuity of a function may be a discrete set, a dense set
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
, or even the entire domain of the function.
This article describes the classification of discontinuities in the simplest case of functions of a single real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variable taking real values.
Classification of discontinuities
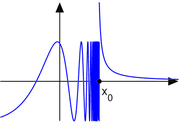
Consider a real valued function ƒ of a real variable x, defined in a neighborhood of the point x0 in which ƒ is discontinuous. Then three situations may be distinguished:- The one-sided limitOne-sided limitIn calculus, a one-sided limit is either of the two limits of a function f of a real variable x as x approaches a specified point either from below or from above...
from the negative direction
and the one-sided limit from the positive direction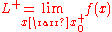
at exist, are finite, and are equal to
exist, are finite, and are equal to  . Then, if ƒ(x0) is not equal to
. Then, if ƒ(x0) is not equal to  , x0 is called a removable discontinuity. This discontinuity can be 'removed to make ƒ continuous at x0', or more precisely, the function
, x0 is called a removable discontinuity. This discontinuity can be 'removed to make ƒ continuous at x0', or more precisely, the function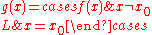
is continuous at x=x0.
- The limits
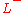 and
and  exist and are finite, but not equal. Then, x0 is called a jump discontinuity or step discontinuity. For this type of discontinuity, the function ƒ may have any value in x0.
exist and are finite, but not equal. Then, x0 is called a jump discontinuity or step discontinuity. For this type of discontinuity, the function ƒ may have any value in x0.
- One or both of the limits
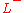 and
and  does not exist or is infinite. Then, x0 is called an essential discontinuity, or infinite discontinuity. (This is distinct from the term essential singularityEssential singularityIn complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
does not exist or is infinite. Then, x0 is called an essential discontinuity, or infinite discontinuity. (This is distinct from the term essential singularityEssential singularityIn complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
which is often used when studying functions of complex variablesComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
.)
The term removable discontinuity is sometimes incorrectly used for cases in which the limits in both directions exist and are equal, while the function is undefined at the point
 This use is improper because continuity
This use is improper because continuityContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and discontinuity of a function are concepts defined only for points in the function's domain. Such a point not in the domain, is properly named a removable singularity.
The oscillation
Oscillation (mathematics)
In mathematics, oscillation is the behaviour of a sequence of real numbers or a real-valued function, which does not converge, but also does not diverge to +∞ or −∞; that is, oscillation is the failure to have a limit, and is also a quantitative measure for that.Oscillation is defined as the...
of a function at a point quantifies these discontinuities as follows:
- in a removable discontinuity, the distance that the value of the function is off by is the oscillation;
- in a jump discontinuity, the size of the jump is the oscillation (assuming that the value at the point lies between these limits from the two sides);
- in an essential discontinuity, oscillation measures the failure of a limit to exist.
Examples

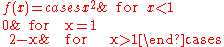
Then, the point
 is a removable discontinuity.
is a removable discontinuity.
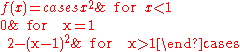
Then, the point
 is a jump discontinuity.
is a jump discontinuity.
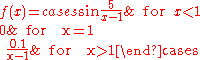
Then, the point
 is an essential discontinuity (sometimes called infinite discontinuity). For it to be an essential discontinuity, it would have sufficed that only one of the two one-sided limits did not exist or were infinite. However, given this example the discontinuity is also an essential discontinuity for the extension of the function into complex variables.
is an essential discontinuity (sometimes called infinite discontinuity). For it to be an essential discontinuity, it would have sufficed that only one of the two one-sided limits did not exist or were infinite. However, given this example the discontinuity is also an essential discontinuity for the extension of the function into complex variables.The set of discontinuities of a function
The set of points at which a function is continuous is always a Gδ setG-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
. The set of discontinuities is an Fσ set
F-sigma set
In mathematics, an Fσ set is a countable union of closed sets. The notation originated in France with F for fermé and σ for somme ....
.
The set of discontinuities of a monotonic function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
is at most countable. This is Froda's theorem
Froda's theorem
In mathematics, Froda's theorem, named after Alexandru Froda, describes the set of discontinuities of a real-valued function of a real variable. Usually, this theorem appears in literature without Froda's name being mentioned. However, this result was first proven by A...
.
Thomae's function is discontinuous at every rational point, but continuous at every irrational point.
The indicator function of the rationals, also known as the Dirichlet function, is discontinuous everywhere
Nowhere continuous
In mathematics, a nowhere continuous function, also called an everywhere discontinuous function, is a function that is not continuous at any point of its domain...
.
See also
- Removable singularity
- Mathematical singularityMathematical singularityIn mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
- Extension by continuity
External links
- "Discontinuity" by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, The Wolfram Demonstrations Project, 2007. - "Discontinuity point" by L. D. Kudryavtsev, Encyclopaedia of MathematicsEncyclopaedia of MathematicsThe Encyclopaedia of Mathematics is a large reference work in mathematics. It is available in book form and on CD-ROM....
.

