
Martingale representation theorem
Encyclopedia
In probability theory
, the martingale representation theorem states that a random variable which is measurable with respect to the filtration generated by a Brownian motion
can be written in terms of an Itô integral with respect to this Brownian motion.
The theorem only asserts the existence of the representation and does not help to find it explicitly; it is possible in many cases to determine the form of the representation using Malliavin calculus
.
Similar theorems also exist for martingales
on filtrations induced by jump processes, for example, by Markov chain
s.
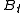 be a Brownian motion
be a Brownian motion
on a standard filtered probability space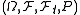 and let
and let 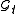 be the augmentation of the filtration generated by
be the augmentation of the filtration generated by 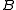 . If X is a square integrable random variable measurable with respect to
. If X is a square integrable random variable measurable with respect to 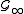 , then there exists a predictable process
, then there exists a predictable process
C which is adapted
with respect to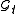 , such that
, such that
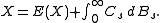
Consequently
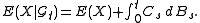
of a hedging strategy.
Suppose that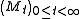 is a Q-martingale process, whose volatility
is a Q-martingale process, whose volatility 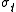 is always non-zero.
is always non-zero.
Then, if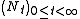 is any other Q-martingale, there exists an F-previsible process
is any other Q-martingale, there exists an F-previsible process 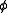 , unique up to sets of measure 0, such that
, unique up to sets of measure 0, such that 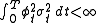 with probability one, and N can be written as:
with probability one, and N can be written as:
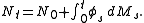
The replicating strategy is defined to be:
where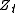 is the stock price discounted by the bond price to time
is the stock price discounted by the bond price to time  and
and 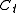 is the expected payoff of the option at time
is the expected payoff of the option at time  .
.
At the expiration day T, the value of the portfolio is: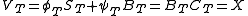
and it's easy to check that the strategy is self-financing: the change in the value of the portfolio only depends on the change of the asset prices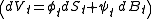 .
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the martingale representation theorem states that a random variable which is measurable with respect to the filtration generated by a Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
can be written in terms of an Itô integral with respect to this Brownian motion.
The theorem only asserts the existence of the representation and does not help to find it explicitly; it is possible in many cases to determine the form of the representation using Malliavin calculus
Malliavin calculus
The Malliavin calculus, named after Paul Malliavin, is a theory of variational stochastic calculus. In other words it provides the mechanics to compute derivatives of random variables....
.
Similar theorems also exist for martingales
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
on filtrations induced by jump processes, for example, by Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s.
Statement of the theorem
Let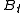 be a Brownian motion
be a Brownian motionBrownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
on a standard filtered probability space
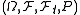 and let
and let 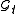 be the augmentation of the filtration generated by
be the augmentation of the filtration generated by 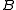 . If X is a square integrable random variable measurable with respect to
. If X is a square integrable random variable measurable with respect to 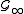 , then there exists a predictable process
, then there exists a predictable processPredictable process
In stochastic analysis, a part of the mathematical theory of probability, a predictable process is a stochastic process which the value is knowable at a prior time...
C which is adapted
Adapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
with respect to
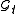 , such that
, such that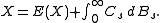
Consequently
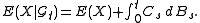
Application in finance
The martingale representation theorem can be used to establish the existenceof a hedging strategy.
Suppose that
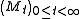 is a Q-martingale process, whose volatility
is a Q-martingale process, whose volatility 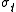 is always non-zero.
is always non-zero.Then, if
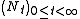 is any other Q-martingale, there exists an F-previsible process
is any other Q-martingale, there exists an F-previsible process 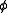 , unique up to sets of measure 0, such that
, unique up to sets of measure 0, such that 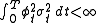 with probability one, and N can be written as:
with probability one, and N can be written as: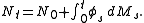
The replicating strategy is defined to be:
- hold
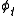 units of the stock at the time t, and
units of the stock at the time t, and - hold
 units of the bond.
units of the bond.
where
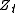 is the stock price discounted by the bond price to time
is the stock price discounted by the bond price to time  and
and 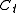 is the expected payoff of the option at time
is the expected payoff of the option at time  .
.At the expiration day T, the value of the portfolio is:
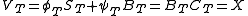
and it's easy to check that the strategy is self-financing: the change in the value of the portfolio only depends on the change of the asset prices
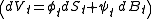 .
.

